浅谈初中数学课堂教学中教师的有效提问

    蔡宏心

    

    

    

    [摘? 要] 现代教育着重强调“学生需具有独立思考的能力，有提出问题、分析问题和解决问题的能力”，而这一目标的达成则需要教师首先具有问题意识，具有有效提问的能力. 因此，教师需捕捉“趣问题”，激发学习兴趣;提炼“真问题”，建构新知识;设计“新问题”，促进思维提升.

    [关键词] 初中数学;问题意识;培养;解决问题的能力

    学生问题意识的培养离不开教师教学理念和教师的有效提问，而教师一旦缺乏问题意识，学生自然也无法形成问题意识. 教师的问题意识是指，在教学过程中，教师能有意识地从教学目标、具体学情等实际出发，以问题引领教学内容，以问题选择教学方法，追求更优质的教育教学效果[1]. 问题不仅可以造就吸引力，还能产生推力，课堂教学中有深度的教师是以具有深度的问题推动课堂教学的. 因此，对于初中数学课堂教学过程而言，问题设计是十分重要的. 在教学实践中，需以课堂为阵地，以教师的提问引领学生的思维，培养学生分析和解决问题的能力. 那么，如何设计有效问题，有效地施教呢？本文笔者以具有典型意义和探究价值的教学片段或一些实施环节为例进行案例分析.

    捕捉“趣问题”，激发学习兴趣

    在教学过程中，教师需善于灵活巧妙地设计问题内容，以一些富有趣味性的问题，贴近学生的生活，融入一些趣味元素，往往能给学生带来新的学习体验，能给课堂教学带来一丝惊喜.

    案例1? 在教学“函数2”的过程中，通过以下生动的“问题串”引领学生了解“函数关系的表示方法”.

    问题1：南宋时候，朱记布庄售卖一种新款布料，每尺面料的价格为6文钱，能否列出关于购买这种新款布料所需的总钱数y（文）与购买总数x（尺）之间的关系式？

    教师在问题设计中融入了激发学生好奇心的穿越情境，由买布的故事达到趣味提问的教学效果，无形中增加了学生对新课学习的热情和想象力. 在充分激趣后，学生思维活跃，很快进入思考状态并探究得出答案. 学生寻得解答后，教师拾级而上，提出问题2：“朱记布庄生意火爆，朱掌柜需匆忙赶往外地进货，留下算账堪忧的朱夫人来营业，你们能帮帮她吗？”经教师点拨，学生根据已学知识想到了“以表格表示金额与数量之间的关系（如表1所示）”来解决，朱夫人的布庄终于可以正常营业了.

    问题解决到此，似乎可以结束了，但教师又适时追问，提出了问题3：“邻居中有个无赖深知朱夫人的底细，想要捉弄她，便去布庄买了2.5尺布料，这可难住了朱夫人，该收多少钱呢？”学生在深度思考和认真讨论后，用“图形表示金额与数量之间的关系（如图1所示）”來解决了这一困境，这样一来，朱夫人依照图像终于可以高枕无忧了.

    在教学中，教师创设巧妙的问题，在学生找不到解决问题突破口时，教师则给予点拨;在面对具有一定思维量的问题时，学生以合作学习的形式一同探索问题. 这样，整节课既连贯又有趣，一环扣一环的问题设计，让学生的探究欲望更加浓厚. 教师借由卖布的过程而促使学生深入思考，拓展分析思路，掌握了函数关系的三种表示方法，并促进了学生的思维深化.

    提炼“真问题”，建构新知识

    教师在课堂教学中，需从学生的生活实际出发，设计真实、自然、贴近学生生活的“真问题”，让学生产生求知欲望，进而去思考、去发现、去创造，让学生获取真实的体验，促进学生的“再创造”[2].

    案例2? 以“函数”的教学片段为例.

    师：今天老师在上班途中给我的爱车加了个油. 在整个加油过程中，我一直在观察，发现显示器上出现了一些有趣的数据变化. 显示器上“7.38元/升”的数据毫无变化，而另外两个小格的数据却不停地变动，你们知道这两个变动的数据是什么吗？

    生1：我知道，其中一个为油量，另一个为金额.

    师：那为什么这两个数据要同时变动呢？

    生2：加油时，油量发生了变化，金额当然也会随之变化了.

    师：很好！那我们一起进入今天的课题“函数”. 我们在加油的过程中，“单价7.38元/升”这一数据保持不变，我们称之为“常量”，变化的油价和金额我们称之为“变量”. 那么你们认为是什么先变化的？

    生3：当然是油量.

    师：很有经验嘛！由于油量的变化导致了金额的变化，因此油量为“自变量”，那金额就为“因变量”，而“因变量”也是“自变量的函数”. 那么，金额就是油量的函数.

    师：若设所加油量为x升，所需付金额为y元，那么两者的函数关系是怎样的呢？

    生4：y=7.38x.

    师：这个式子就是函数关系式. 现在我的汽车油箱最多只能装400升的汽油，那么自变量x的取值范围是？

    生5：0≤x≤400.

    ……

    就这样，“函数”这一概念就在“加油”这一学生熟悉和亲身体验过的问题情境中轻松地传授了. 在这个教学过程中，学生不仅习得了数学知识技能，更感悟到了数学的价值，从而使学生真正地亲近数学、喜爱数学，掌握相关的思维模式.

    设计“新问题”，促进思维提升

    设计引发学生探究的“新”问题情境也是非常常见的提问方式，在这样的提问过程中，教师同样可以充足融入趣味性的元素，让学生的兴趣更加浓厚. 当然，问题的设计需少而精，并符合教学实际.

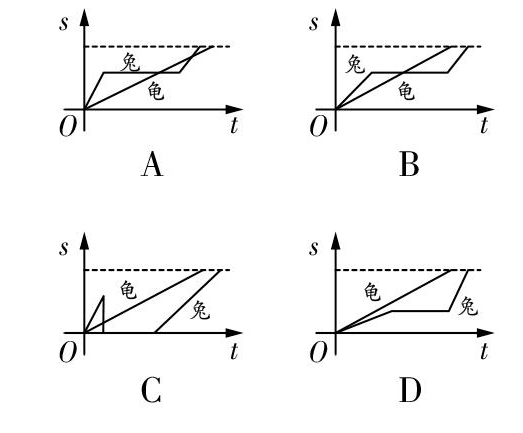
    案例3? 在学习完“一次函数”后，笔者安排了以下这道选择题：乌龟和兔子赛跑，同时在一棵大树后出发，很快兔子就把乌龟远远地甩在身后. 兔子瞬间骄傲起来，慢慢降下了速度，心想：“我睡一觉估计它都赶不上. ”果然，它倚在一棵大树边呼呼大睡了起来，乌龟一直爬啊爬，终于超过了兔子. 当兔子一觉睡醒，发现乌龟已经快到达终点了，它拼命追赶还是输给了乌龟. 以下图像代表龟兔比赛中行走的路程s随时间t的变化情况，这四个选项中能大致反映其变化的是（? ? ? ）

    经过思考和探究，大部分学生选择了选项B，也有一小部分学生选择了选项A. 基于这些结果，笔者尝试做了如下创造性的延伸：首先，请选A的学生阐述理由，并充分肯定其对兔子和乌龟的运动过程的正确认识，并提示“兔子是输给了乌龟吗？图像上是如何体现的呢？”笔者沿着图像又请学生观察选项D并为其打造故事情节. 这一生动的问题情境，极大地激发了学生的兴趣，学生的“脑洞”大开，编出了故事：“一天，一只成年乌龟和一只刚会行走的小兔约定进行赛跑，小兔由于体力不支，只能跑跑停停，就这样再三反复地前进;乌龟奋力前进，一分钟也不休息，终于赢得了冠军. ”通过对故事情节的描述，学生加深了对新知识的理解和巩固. 接着，再回到选项C，笔者继续引导学生讨论，经过一番激烈的讨论，学生得出“选项C不可能发生”的结论. 最后，笔者让同桌两人一组，一人先画出函数图像，另一人根据图像创编“新龟兔赛跑”的故事;再由一人创编故事，另一人画出函数图像;接着，请创意新颖的组别表演展示.

    这样，才能充分发挥学生的主体地位，才能让所有学生对一次函数的图像与意义有更深层次的理解，同时也进一步培养了学生的创新思维.

    总之，在课堂教学中，教师给学生带来的思维空间越广阔，其思维成果则越丰厚，智力水平则越可观. 作为一名一线数学教师，在教学中若想有成效地教学，培养学生的问题意识，提升学生的思维能力，就必须从实际出发，不断地创新教学方法，以科学的教学手段培养现代社会需要的具有高阶思维能力的人才，不断地攀升数学课程改革的新高度[3].

    参考文献：

    [1]张奠宙，张荫南. 新概念：用问题驱动的数学教学[J]. 高等数学研究，2004（05）.

    [2]李鹏，傅赢芳. 论数学课堂提问的误区与对策[J]. 数学教育学报，2013，22（04）.

    [3]温建红. 数学课堂有效提问的内涵及特征[J]. 数学教育学报，2011，20（06）.