初中物理教学中学生数理能力的培养
肖庆新
摘 要:初中物理教学中培养学生的数理能力,既是突出物理课程性质特点,又是顾及学生对初高中物理学习的有效衔接。培养途径及方法为:利用概念建构,训练学生的数理语言描述能力;加强审题教学,发展学生的数理模型构建能力;借助复杂问题,提升学生的数理方法运用能力。在课标要求的基础上要适当拔高,但教师要注意把握好拔高的“度”,其原则就是“顾及课堂,放手课外,宜练不宜考”。
关键词:数理能力;数理语言;数理模型;数理方法
数学作为定量描述的工具,其知识与方法渗透并贯穿于整个物理课程,为物理概念、定律的表述提供简洁、精炼的形式语言,为学生进行抽象思维和逻辑推理提供有效的方法[1]。数理能力,指运用数学知识与方法来描述和分析物理问题的能力。初中物理仅定性研究一些简单的物理现象,其中牵涉到的定量分析也是一些简单的计算,这种课程要求在一定的程度上淡化了对学生数理能力的培养。然而高中物理侧重于定量研究,学生的数理能力是学好物理的先决条件。因此,初中物理教学中培养学生的数理能力,既是突出物理课程性质特点,又是顾及学生对初高中物理学习的有效衔接。笔者就学生数理能力培养课题,谈谈个人的研究收获。
1 利用概念建构,训练学生的数理语言描述能力
数理语言主要包括文字语言、符号语言、图形语言三类[1]。对于物理概念(包括物理规律),一般都可以用这三种语言来描述。如密度概念:在文字语言方面,它可以表述为“物体的质量与其体积的比值”;在符号语言方面,它可以表示为“ρ=m/V”;在图形语言方面,它可以描述为仅在第一象限m∝V的正比例图线。
运用数理语言来描述物理量之间的关系是数理能力中首要的也是最基本的能力。数学形式建立后,物理问题的定量分析与计算就有着相应的工具,逻辑推理也有着一定的依据,因此,培养学生用数学语言来描述物理问题的能力是培养学生数理能力的首要方面。
利用概念建构过程来培养学生的数学语言描述能力是课堂教学的最佳契机。首先是让学生尝试用文字性的语言来表述概念或规律。如在“阿基米德原理”实验中,学生通过对实验数据的分析,发现数据表格中的浮力数值等于所排开水重力数值,这时就可以要求学生文字语言来描述浮力原理。对于教材中“浸入液体中的物体所受浮力的大小等于物体排开的液体所受重力的大小”的表述,学生可能会漏掉“浸入液体中”、“大小”等重要词语或表述不精炼,但只要教学中加以补充或修正,那么学生不仅能领悟数学语言的准确性与精炼性,而且还能促进学生领悟物理语言的科学性,从而促使学生的数理语言得到协调性的发展。其次是引导学生把文字语言表述转化为数学符号语言。如阿基米德原理,教学中就可以要求学生写出F浮=ρ液gV排。当然,学生也可能会写出F浮=G排液 或 F浮=m排g等形式,然而这些都是阿基米德原理的数学形式,这种训练效益毋庸置疑。其三是引导学生用图形语言来描述概念或规律。以F浮为纵坐标,G排液或m排液g为横坐标,F浮=G排液与F浮=m排液g都是正比例图象,其中图象“为什么仅局限于第一象限”和“为什么两直线陡度不同”的问题又会促进学生的深入思考。对于F浮=ρ液gV排,可以用把F浮视为ρ液的函数,也可以可以用把F浮视为V排的函数,但前提条件是V排或ρ液保持不变,这就是控制变量思想的具体运用。如果学生能领悟上述内涵,那么这何以不是“以数促理”的学习效益。
在初中物理教材中,有不少的物理概念仅是用文字表述,这些都是训练学生数理能力的课程资源。如“牛顿第一定律”,学生如果能用“F=0,Δv=0”的形式来表述,这何以不是一种简洁的数理思维。再如“折射规律”,如果学生能用正比例图线来描述折射角γ(纵坐标)和入射角i(横坐标)的大小关系:若光由空气射入其它介质,图线斜率小于1;若光由其它介质射入空气,图线斜率大于1;那么这何以不是一种深刻的数理思维。诚然,折射定律是sinγ∝sini,而学生混淆为γ∝i,虽有欠缺,但從数理思维而言,仍是一种创造性的思维。
2 加强审题教学,发展学生的数理模型构建能力
物理学习主要包括“知识建构”和“知识应用”两个过程,运用数学语言来描述概念仅是用于知识建构,更重要的学习是在“知识应用”中能发挥数理能力来解决物理问题。
数理能力,首先是数学模型构建。所谓数理模型,就是依据物理概念与物理规律和其中蕴含的数量关系而把物理问题转化为数学问题[1]。在数理模型建构中,问题情景的不同,构建数理模型的方法也各不相同,其中问题归类与寻找数量关系是数理模型构建中的两项重点工作。问题归类,指把当前的问题划归到某一物理知识块问题,是液体压强问题还是浮力问题,是二力平衡问题还是做功问题,等等。一旦正确归类,那么学生就自然明确会牵涉到哪些知识或方法,解题就有着明确的方向或思路。寻找数量关系,就是指依据问题情境来分析某些物理量之间的数量关系,它可能是元件结构关系,也可能是几何条件关系,还可能是某种原理关系,等等。能否进行问题归类与正确地寻找数量关系,审题是关键。因此,加强审题教学是培养学生数理模型构建能力的重要途径。下面举例说明。
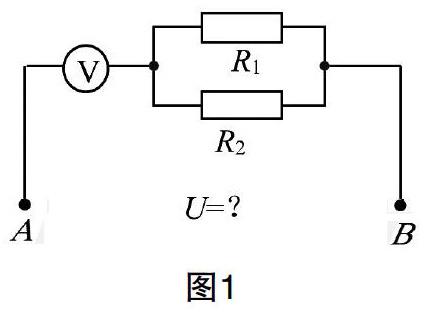
【例题1】某电压表的量程为0-3V,如给该电压表串联一个电阻R1,则电路A、B两端允许的最大电压为5V;如给该电压表串联一个电阻R2,则电路A、B两端允许的最大电压为6V。现将电阻R1和R2并联后再与该电压表串联,如图1所示,则此时电路A、B两端允许的最大电压U为:
A.3.5V B.4.0V C.4.2V D.4.5V
本题属于电表的改装问题,初中学生不具备这方面知识,教学中只能引导学生把本题归类为电路的串并联问题。
在审题中,首先学生会产生两个困惑:一是电压表怎么能与电阻串联?二是A、B两端电压怎么会变化?其次是不能正确领会“A、B两端允许的最大电压”文字中隐含的条件是“电压表两端电压值是3V”。其三是对本题的问题情境会混淆不清。本题共三句话,每一句话对应的是一种电路状态,对于数理模型构建来说,其中一句话就可以建立一个方程。
就本题而言,加强审题教学,就是指注重引导学生弄清楚以上所说的几个问题,具体的教学做法就是提出以下系列问题促进学生的审题思考:①把某一电阻接入含有其它用电器的电路,如果电路中电流不变,接入的电阻越大,该电阻两端的电压大小怎样?②电压表能否视为一个大电阻的用电器?③图1中A、B两端是否是接在电源两端?④A、B两端达到最大电压时,电压表的电压值是多少?⑤本题牵涉到了哪几种电路?你能画出它们的电路图吗?显然,学生弄清楚了上述问题,一般都可以列出题目涉及的三种电路的三个数理方程。本问题的数理模型就如此建立起来了。
在物理解题中,数理模型的建立过程,既是问题归类并对已有知识与方法的检索过程,又是解题思路与方案形成的酝酿过程。可见,它关键取决于学生的审题能力。
3 借助复杂问题,提升学生的数理方法运用能力
物理问题,要定量分析,就离不开数学。初中物理知识虽属简单,但也可以通过创设一些问题情境使得问题复杂化,而解决这方面的问题完全取决于学生的数理方法运用能力。所谓数理方法,这里指数学解决物理问题的方法。下面举例说明。
【例题2】某同学在斜向上运动的电梯上,以相对电梯不变的速度,从二楼走到一楼,数得电梯阶级为60,从一楼走到二楼,数得电梯阶级为20,求从一楼到二楼电梯的级数。
从物理知识来讲,本题属于匀速运动和相对运动问题,较简单,然而题目给出的已知信息只有上楼数的60级阶梯与下楼数的20级阶梯,似乎条件不足,因而多数学生无法解答。
解答本题,主要涉及数理模型构建与数理方法运用这两方面的能力。在数理模型构建方面,对于条件不足,可以假设某些物理量,然后再借助这些物理量建立有关数理方程。
数理模型构建:设从一楼到二楼电梯的级数为N,电梯的运动速度为每秒x个阶梯,人的运动速度为每秒y个阶梯。那么由一楼到达二楼人相对地面的速度为(x+y)/s,所需时间为t1=N/(x+y),则人由一楼到达二楼过程数的阶梯级数方程为:Ny/(x+y)=20……(1)
由二楼到达一楼人相对地面的速度为(y-x)/s(y>x,否则人不能到达一楼),所需时间为t2=N/(y-x),则人由二楼到达一楼过程数的阶梯级数方程为:Ny/(y-x)=60……(2)
数理方法运用:上面两个方程含有x、y、N三个未知数,多数学生不会求解。似乎“山穷水尽疑无路”,然而我们只要将上面两个方程左边的分子分母同除以y,那么两个方程仅含有x/y与N这两个未知数。“柳暗花明又一村”,联解方程组得N=30。
这就是数理方法运用能力在物理解题中的重要性!
在物理解題中,数理方法运用能力还重点体现在图象分析方面。请看下例:
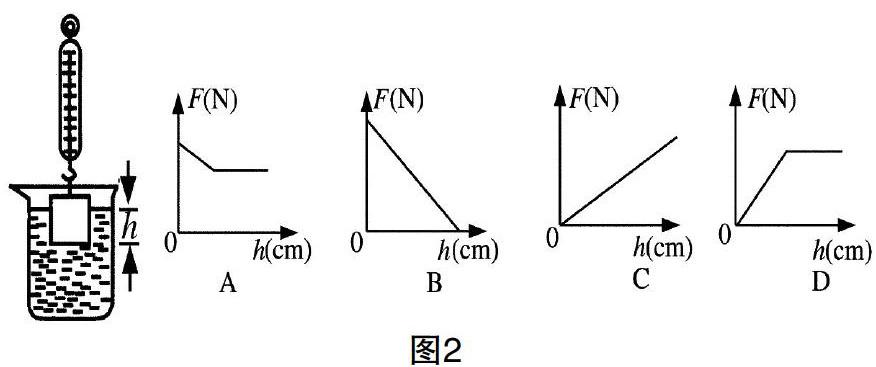
【例题3】如图2所示,将一个挂在弹簧测力计下的圆柱体金属块缓慢浸入水中(水足够深),在圆柱体接触到容器底之前,能正确地反应出弹簧测力计示数F和圆柱体下表面到水面距离h的关系的图是:
数学模型建构:依据三力平衡条件与阿基米德原理,弹簧测力计示数F与h的函数关系式可写为F=G-ρgV排,从函数式可以看出,F随着V排增大而减小,当金属块全部浸没后,V排保持不变,即F也保持不变,正确选项为A。
这两例都属于复杂的问题,超出了课标对学生数理能力要求,但从培养学生的数理能力或做好初高中物理教学衔接过渡而言,这种“以借助复杂问题来促进数理思维”的教学做法却有着重要的价值意义,这也正是贯彻落实“关注学生发展”课程理念的体现。
关于数理能力的培养,初中物理课标要求较低,然而在培养方面,笔者却主张在课标要求的基础上要适当拔高,故教学中教师要注意把握好拔高的“度”,其原则就是“顾及课堂,放手课外,宜练不宜考”。具体可表述为:课堂注重训练学生的数理语言能力,加强审题教学以培养学生的数理模型构建能力,而数学方法运用能力留于课外自主训练,对学生不作统一的硬性要求,平时考试仅稍有出现或完全不考。
参考文献:
[1]王溢然.中学物理数学方法讲座〔M〕合肥:中国科学技术大学出版社,2017.


摘 要:初中物理教学中培养学生的数理能力,既是突出物理课程性质特点,又是顾及学生对初高中物理学习的有效衔接。培养途径及方法为:利用概念建构,训练学生的数理语言描述能力;加强审题教学,发展学生的数理模型构建能力;借助复杂问题,提升学生的数理方法运用能力。在课标要求的基础上要适当拔高,但教师要注意把握好拔高的“度”,其原则就是“顾及课堂,放手课外,宜练不宜考”。
关键词:数理能力;数理语言;数理模型;数理方法
数学作为定量描述的工具,其知识与方法渗透并贯穿于整个物理课程,为物理概念、定律的表述提供简洁、精炼的形式语言,为学生进行抽象思维和逻辑推理提供有效的方法[1]。数理能力,指运用数学知识与方法来描述和分析物理问题的能力。初中物理仅定性研究一些简单的物理现象,其中牵涉到的定量分析也是一些简单的计算,这种课程要求在一定的程度上淡化了对学生数理能力的培养。然而高中物理侧重于定量研究,学生的数理能力是学好物理的先决条件。因此,初中物理教学中培养学生的数理能力,既是突出物理课程性质特点,又是顾及学生对初高中物理学习的有效衔接。笔者就学生数理能力培养课题,谈谈个人的研究收获。
1 利用概念建构,训练学生的数理语言描述能力
数理语言主要包括文字语言、符号语言、图形语言三类[1]。对于物理概念(包括物理规律),一般都可以用这三种语言来描述。如密度概念:在文字语言方面,它可以表述为“物体的质量与其体积的比值”;在符号语言方面,它可以表示为“ρ=m/V”;在图形语言方面,它可以描述为仅在第一象限m∝V的正比例图线。
运用数理语言来描述物理量之间的关系是数理能力中首要的也是最基本的能力。数学形式建立后,物理问题的定量分析与计算就有着相应的工具,逻辑推理也有着一定的依据,因此,培养学生用数学语言来描述物理问题的能力是培养学生数理能力的首要方面。
利用概念建构过程来培养学生的数学语言描述能力是课堂教学的最佳契机。首先是让学生尝试用文字性的语言来表述概念或规律。如在“阿基米德原理”实验中,学生通过对实验数据的分析,发现数据表格中的浮力数值等于所排开水重力数值,这时就可以要求学生文字语言来描述浮力原理。对于教材中“浸入液体中的物体所受浮力的大小等于物体排开的液体所受重力的大小”的表述,学生可能会漏掉“浸入液体中”、“大小”等重要词语或表述不精炼,但只要教学中加以补充或修正,那么学生不仅能领悟数学语言的准确性与精炼性,而且还能促进学生领悟物理语言的科学性,从而促使学生的数理语言得到协调性的发展。其次是引导学生把文字语言表述转化为数学符号语言。如阿基米德原理,教学中就可以要求学生写出F浮=ρ液gV排。当然,学生也可能会写出F浮=G排液 或 F浮=m排g等形式,然而这些都是阿基米德原理的数学形式,这种训练效益毋庸置疑。其三是引导学生用图形语言来描述概念或规律。以F浮为纵坐标,G排液或m排液g为横坐标,F浮=G排液与F浮=m排液g都是正比例图象,其中图象“为什么仅局限于第一象限”和“为什么两直线陡度不同”的问题又会促进学生的深入思考。对于F浮=ρ液gV排,可以用把F浮视为ρ液的函数,也可以可以用把F浮视为V排的函数,但前提条件是V排或ρ液保持不变,这就是控制变量思想的具体运用。如果学生能领悟上述内涵,那么这何以不是“以数促理”的学习效益。
在初中物理教材中,有不少的物理概念仅是用文字表述,这些都是训练学生数理能力的课程资源。如“牛顿第一定律”,学生如果能用“F=0,Δv=0”的形式来表述,这何以不是一种简洁的数理思维。再如“折射规律”,如果学生能用正比例图线来描述折射角γ(纵坐标)和入射角i(横坐标)的大小关系:若光由空气射入其它介质,图线斜率小于1;若光由其它介质射入空气,图线斜率大于1;那么这何以不是一种深刻的数理思维。诚然,折射定律是sinγ∝sini,而学生混淆为γ∝i,虽有欠缺,但從数理思维而言,仍是一种创造性的思维。
2 加强审题教学,发展学生的数理模型构建能力
物理学习主要包括“知识建构”和“知识应用”两个过程,运用数学语言来描述概念仅是用于知识建构,更重要的学习是在“知识应用”中能发挥数理能力来解决物理问题。
数理能力,首先是数学模型构建。所谓数理模型,就是依据物理概念与物理规律和其中蕴含的数量关系而把物理问题转化为数学问题[1]。在数理模型建构中,问题情景的不同,构建数理模型的方法也各不相同,其中问题归类与寻找数量关系是数理模型构建中的两项重点工作。问题归类,指把当前的问题划归到某一物理知识块问题,是液体压强问题还是浮力问题,是二力平衡问题还是做功问题,等等。一旦正确归类,那么学生就自然明确会牵涉到哪些知识或方法,解题就有着明确的方向或思路。寻找数量关系,就是指依据问题情境来分析某些物理量之间的数量关系,它可能是元件结构关系,也可能是几何条件关系,还可能是某种原理关系,等等。能否进行问题归类与正确地寻找数量关系,审题是关键。因此,加强审题教学是培养学生数理模型构建能力的重要途径。下面举例说明。
【例题1】某电压表的量程为0-3V,如给该电压表串联一个电阻R1,则电路A、B两端允许的最大电压为5V;如给该电压表串联一个电阻R2,则电路A、B两端允许的最大电压为6V。现将电阻R1和R2并联后再与该电压表串联,如图1所示,则此时电路A、B两端允许的最大电压U为:
A.3.5V B.4.0V C.4.2V D.4.5V
本题属于电表的改装问题,初中学生不具备这方面知识,教学中只能引导学生把本题归类为电路的串并联问题。
在审题中,首先学生会产生两个困惑:一是电压表怎么能与电阻串联?二是A、B两端电压怎么会变化?其次是不能正确领会“A、B两端允许的最大电压”文字中隐含的条件是“电压表两端电压值是3V”。其三是对本题的问题情境会混淆不清。本题共三句话,每一句话对应的是一种电路状态,对于数理模型构建来说,其中一句话就可以建立一个方程。
就本题而言,加强审题教学,就是指注重引导学生弄清楚以上所说的几个问题,具体的教学做法就是提出以下系列问题促进学生的审题思考:①把某一电阻接入含有其它用电器的电路,如果电路中电流不变,接入的电阻越大,该电阻两端的电压大小怎样?②电压表能否视为一个大电阻的用电器?③图1中A、B两端是否是接在电源两端?④A、B两端达到最大电压时,电压表的电压值是多少?⑤本题牵涉到了哪几种电路?你能画出它们的电路图吗?显然,学生弄清楚了上述问题,一般都可以列出题目涉及的三种电路的三个数理方程。本问题的数理模型就如此建立起来了。
在物理解题中,数理模型的建立过程,既是问题归类并对已有知识与方法的检索过程,又是解题思路与方案形成的酝酿过程。可见,它关键取决于学生的审题能力。
3 借助复杂问题,提升学生的数理方法运用能力
物理问题,要定量分析,就离不开数学。初中物理知识虽属简单,但也可以通过创设一些问题情境使得问题复杂化,而解决这方面的问题完全取决于学生的数理方法运用能力。所谓数理方法,这里指数学解决物理问题的方法。下面举例说明。
【例题2】某同学在斜向上运动的电梯上,以相对电梯不变的速度,从二楼走到一楼,数得电梯阶级为60,从一楼走到二楼,数得电梯阶级为20,求从一楼到二楼电梯的级数。
从物理知识来讲,本题属于匀速运动和相对运动问题,较简单,然而题目给出的已知信息只有上楼数的60级阶梯与下楼数的20级阶梯,似乎条件不足,因而多数学生无法解答。
解答本题,主要涉及数理模型构建与数理方法运用这两方面的能力。在数理模型构建方面,对于条件不足,可以假设某些物理量,然后再借助这些物理量建立有关数理方程。
数理模型构建:设从一楼到二楼电梯的级数为N,电梯的运动速度为每秒x个阶梯,人的运动速度为每秒y个阶梯。那么由一楼到达二楼人相对地面的速度为(x+y)/s,所需时间为t1=N/(x+y),则人由一楼到达二楼过程数的阶梯级数方程为:Ny/(x+y)=20……(1)
由二楼到达一楼人相对地面的速度为(y-x)/s(y>x,否则人不能到达一楼),所需时间为t2=N/(y-x),则人由二楼到达一楼过程数的阶梯级数方程为:Ny/(y-x)=60……(2)
数理方法运用:上面两个方程含有x、y、N三个未知数,多数学生不会求解。似乎“山穷水尽疑无路”,然而我们只要将上面两个方程左边的分子分母同除以y,那么两个方程仅含有x/y与N这两个未知数。“柳暗花明又一村”,联解方程组得N=30。
这就是数理方法运用能力在物理解题中的重要性!
在物理解題中,数理方法运用能力还重点体现在图象分析方面。请看下例:
【例题3】如图2所示,将一个挂在弹簧测力计下的圆柱体金属块缓慢浸入水中(水足够深),在圆柱体接触到容器底之前,能正确地反应出弹簧测力计示数F和圆柱体下表面到水面距离h的关系的图是:
数学模型建构:依据三力平衡条件与阿基米德原理,弹簧测力计示数F与h的函数关系式可写为F=G-ρgV排,从函数式可以看出,F随着V排增大而减小,当金属块全部浸没后,V排保持不变,即F也保持不变,正确选项为A。
这两例都属于复杂的问题,超出了课标对学生数理能力要求,但从培养学生的数理能力或做好初高中物理教学衔接过渡而言,这种“以借助复杂问题来促进数理思维”的教学做法却有着重要的价值意义,这也正是贯彻落实“关注学生发展”课程理念的体现。
关于数理能力的培养,初中物理课标要求较低,然而在培养方面,笔者却主张在课标要求的基础上要适当拔高,故教学中教师要注意把握好拔高的“度”,其原则就是“顾及课堂,放手课外,宜练不宜考”。具体可表述为:课堂注重训练学生的数理语言能力,加强审题教学以培养学生的数理模型构建能力,而数学方法运用能力留于课外自主训练,对学生不作统一的硬性要求,平时考试仅稍有出现或完全不考。
参考文献:
[1]王溢然.中学物理数学方法讲座〔M〕合肥:中国科学技术大学出版社,2017.

