对两道动态问题的剖析与思考
毕先江


[摘? 要] 新课标大纲提出,要求学生掌握图形的基本性质、图形运动变换的规律及对应关系,提升学生对数量关系和空间几何的认识. 而由此衍生的动态几何问题成为近几年中考的重难点题型,该类考题具有运动特性,包含一定的不确定条件,可有效考查學生的分析思维. 文章以两道动态考题为例,分析解题思路,总结解题策略,提出相应的教学建议,与读者交流.
[关键词] 动态几何问题;课堂教学;动点;旋转
问题呈现及思路突破
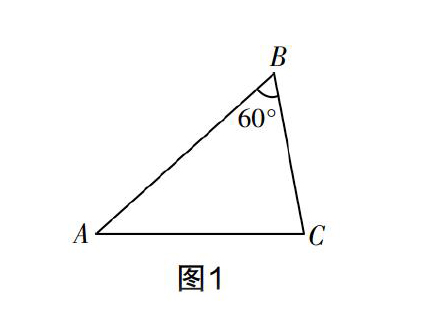
考题1? 如图1,在△ABC中,∠B=60°,BA=24 cm,BC=16 cm.
(1)在点A处有一动点P,它将沿着射线AB的方向运动;同时在点C处有一动点Q,它将沿着射线CB的方向运动. 设动点P的速度为4 cm/s,动点Q的速度为2 cm/s,若两动点同时开始运动,设运动时间为t s,则当 t为何值时,△PBQ的面积与△ABC面积的比为1 ∶ 2?
(2)在第(1)问的条件下,试求点P和点Q之间的距离.
思路突破? (1)由条件可知点P和点Q分别为从点A和点C出发的动点,分别沿着各自的方向运动,由于运动速度不同,故两点的位置会出现以下三种情形:①当0
在BC边上取一点Q,作HQ⊥AB于点H,再过点C作CG⊥AB于点G,如图2所示,则线段HQ和CG分别为△PBQ和△ABC的一条边上的高. 可求得S△ABC=AB·CG=96. S△PBQ=BP·QH,其中BP=24-4t,QH=(8-t),所以S△PBQ=(24-4t)·(8-t). 由=,得(24-4t)·(8-t)=×96,可解得t1=2,t2=12(舍去). 所以当t为2时,△PBQ的面积与△ABC面积的比为1 ∶ 2.
(2)在第(1)问成立的条件下求该问,可将t=2代入,求得点P和点Q的具体位置,即HQ=6,BQ=12,BP=16,进而可得BH=6,PH=10. 求P和点Q之间的距离,实际上就是求线段PQ的长,可将其放在Rt△PQH中,由直角三角形的勾股定理可得PQ2=HQ2+PH2,从而可解得PQ=4,即点P和点Q之间的距离为4.
考题2? 已知△ABC为等腰三角形,AB=AC=5,∠ABC的余弦值为,现将△ABC绕着点C顺时针旋转,可得△A1B1C. 回答下列问题:
(1)若旋转后的点B1位于线段BA的延长线上,如图3所示,①试证明BB1∥CA1;②试求△AB1C的面积.
(2)点E为线段BC的中点,点F为线段AB上一动点,若△ABC绕点C顺时针旋转的过程中点F的对应点为F1,如图4,设EF1长度的最大值为a,最小值为b,试求a-b的值.
思路突破? (1)①要证BB1∥CA1,分析可知需要利用“内错角相等,两直线平行”来完成,即∠B1CA1=∠BB1C,因此需要利用条件构建起两角的等量关系. 已知等腰三角形ABC中,AB=AC,△ABC绕着点C顺时针旋转得到了△A1B1C,则∠B=∠ACB,BC=B1C,∠B1CA1=∠ACB. 由BC=B1C可得∠BB1C=∠B,所以∠B1CA1=∠BB1C. 进而可得BB1∥CA1.
②求△AB1C的面积,可以将其视为是以B1A为底的一般三角形. 如图5,过点C作BB1的垂线,垂足为E,则S△AB1C=AB1·EC,只需要求出AB1和EC的长度即可.
过点A作AG⊥BC于点G,由等腰三角形的性质可知BG=CG,cos∠ABC==,已知AB=5,则BG=3. 所以BC=B1C=6,进而可求得BE=B1E=,BB1=,CE=. 所以AB1=. S△AB1C=××=,即△AB1C的面积为.
(2)本小问求等腰三角形ABC绕固定点旋转过程中EF1长度最大值和最小值的差,只需要分别确定EF1的最大值和最小值即可,属于动态最值问题,可以模拟△ABC上几个关键点的轨迹. 定点到线段的垂线段最短. 如图6,过点C作CF⊥AB,垂足为F,点F在运动过程中的对称点为点F1,分别以点C为圆心,以CB和CF为半径画圆,如图6所示,则在内圆上存在EF1的最值. 由图形可知,BC与圆的交点就为EF1的最小值点,BC的延长线与外圆的交点F1′ 就为EF1的最大值点. 已知△BFC为直角三角形,其中CF=,则CF1=CF=,则EF1的最小值b=CF1-EC=,EF1的最大值a=EC+CF1′ =3+6=9,所以a-b=9-=.
试题特点及解法剖析
上述两道考题均属于初中数学典型的动态几何问题,该类问题最为典型的特点就是以几何动点或图形的平移旋转为背景实现图形的运动变化,使得问题的几何条件处于变化状态,因此题中蕴含大量的信息,求解时需要采用特定的解题策略. 而上述两道考题的转化和建模方式就是基于特定问题所采用的具有代表性的方法.
策略一:构建模型,“动”中有“定”
考题1以动点为依托,构建了对应的动态三角形,要求分析特定面积关系的动点时刻,分析的重点有两个:一是必须构建相应的面积模型,二是由于题目给出了动点的运动速度,需要利用相应的公式建立速度、时间与线段长的关系. 虽然考题中含有动点,但从总体上来看依然属于几何面积问题,即动点中存在“定”模型,因此可以依托几何的面积模型构建相应的解题思路,即利用线段长=动点速度×运动时间,建立起动点位置与几何面积之间的关系. 对于综合数学模型的动态几何问题,可以首先分析动点的位置,然后结合相应的模型将问题转化为方程或者函数问题,通过分析函数或解方程的方式来求解.
策略二:分析关键位置,“动”中取“静”
动态几何问题的另一种重要解题策略是化“动”為“静”或“动”中取“静”,即把握几何运动过程中的几个关键位置,通过分析其中的关键位置来突破考题. 如上述考题2以图形旋转为基础,构建了相应的动态背景,第(2)问求线段EF1最大值与最小值的差值,显然需要分析图形运动的特点来确定这两个特殊位置. 因此问题分析时需要充分利用图形旋转的特点——图形的形状、对应边、对应角不变,利用几何圆研究线段最值的便利性来获取特殊位置. 上述解题过程利用旋转特点获得了关键的几何条件,通过绘制几何圆确定了关键点的运动轨迹,利用直观的图形达到了定点、定位的目的. 因此,对于以图形运动为基础的动态几何问题,可以首先分析图形运动过程中的不变条件,把握图形中关键点的运动轨迹,从而获得图形运动的关键位置,最后结合几何知识破解.
动态问题思考与建议
几何动态问题作为中考的关键题型,对学生的思维能力和综合知识有着较高的要求,问题中的点动和形动是最常见的方式,但分析动点的运动规律或轨迹、构建相应的几何关系或数量关系才是重点,因此动态问题的条件提取、静态转化才是解题的关键. 下面提出几点建议.
1. 立足问题生长点,牢实基础知识
动态问题的命题背景一般为点的运动和图形运动,其中几何的性质定理、图形的运动规律是问题突破的基础,同时还需要学生熟悉基本图形,能够从复合图形中提取特殊图形,如等腰三角形、直角三角形等. 如上述考题在求解时利用了等边对等角性质、勾股定理、旋转特性等,因此课堂教学时需要教师关注学生的基础,以提升学生灵活运用基础知识的能力为教学重点. 另外,动态问题中涉及了一些几何的通性通法,如求几何面积的技巧、几何中分析线段最值的方法等,这些最基本的方法对于问题突破极为重要,合理使用可以取得良好的解题效果,教学中需要教师重点讲解,以提升学生的解题能力.
2. 把握动态规律,总结解题策略
动态问题与其他综合性考题相比,最为突出的特点在于图形中存在变化、不确定因素,需要采用变换思维来分析问题,包括提取图形变化的性质、动点运动的规律,以及动态问题中的不变条件. 而在构建解题思路时,则需要采用一定的策略,如通过动静结合的观点建立动态和静态条件之间的联系,探寻动态问题中的变量构建相应的模型,研究动态问题中的特殊位置,这些解题策略对于提升学生的解题效率有着极大的帮助. 因此,在教学中,教师需要遵从问题发展、衍生的规律,引导学生从最基本的问题入手,观察图形特点,总结动态问题的特点及分析方法,逐步帮助学生形成解题的基本思路和策略. 同时,注重在解题中渗透数学思想方法,促进学生思维水平的发展.

