基于数学基本活动经验积累的教学研究

    顾君

    

    

    [摘? 要] 文章以“三角尺拼角”一课为例，进行了有效积累数学基本活动经验途径的教学研究. 笔者基于数学基本活动经验积累的课堂教学实践与思考，从四个层面来探究数学实验在初中数学课堂教学中的活动经验积累.

    [关键词] 数学基本活动经验;数学实验;三角尺拼角

    数学基本活动经验既是学生在数学活动中直接获得的经验，也是学生在不断思考和反复探究之后提炼的个人认知，其最高层次为形成数学的直观能力. 因此，帮助学生积累数学基本活动经验是教师进行教学的重要目标之一. 而数学实验作为积累数学基本活动经验的有效载体，近年来已成为一个热门的研究话题. 笔者以七上《初中数学实验手册》中的“三角尺拼角”一课为例，从经验激活、经验积累、经验迁移和经验升华四个层面来探究数学实验在初中数学课堂教学中活动经验积累的设计与思考.

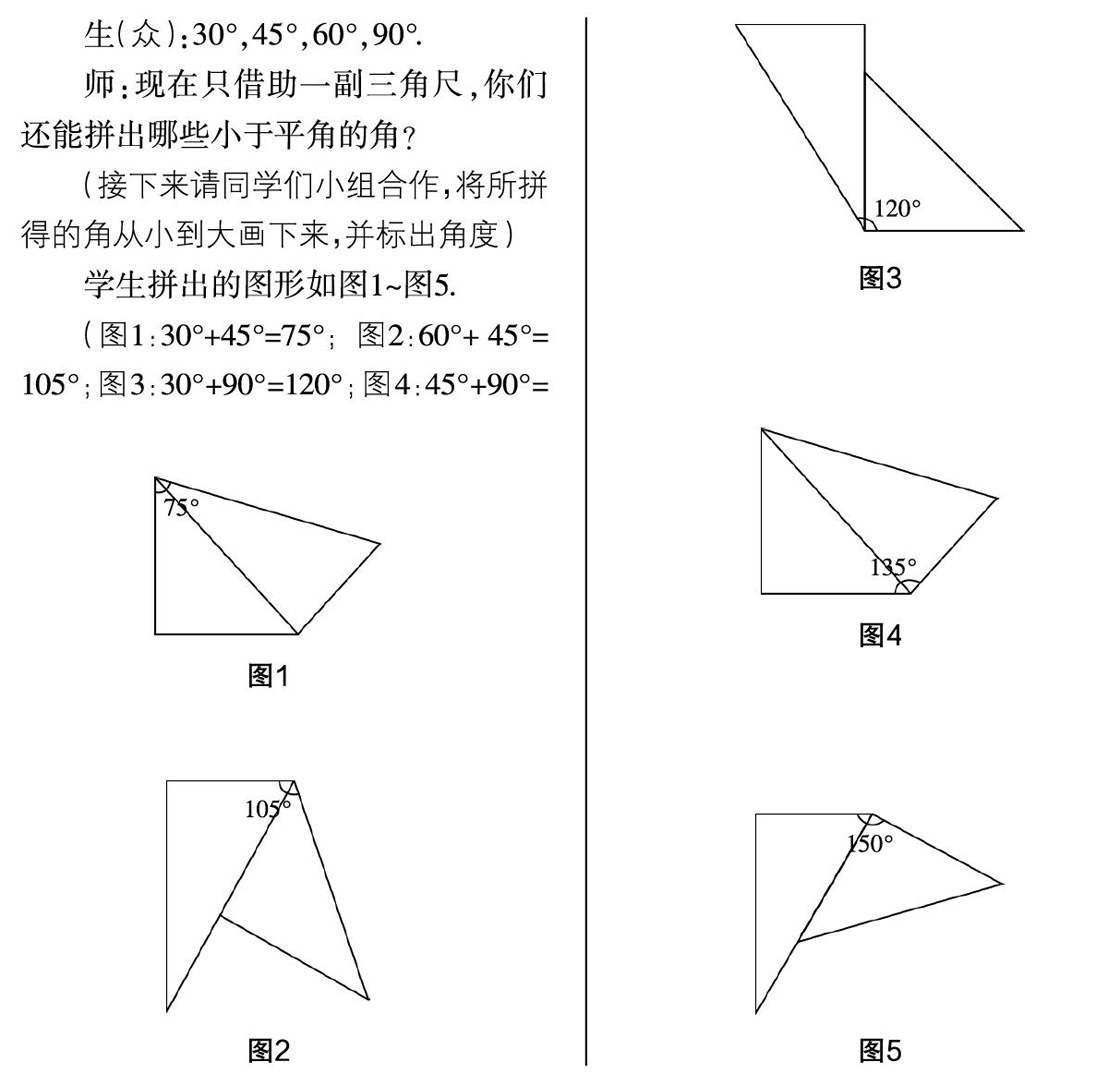
    师：这位同学讲得非常好. 用三角尺拼角包含两种方法，一种是“拼”，另一种是“叠”. 这里的“拼”就是数学上的“补”，“叠”就是“割”，合起来就是“割补”. 那我们如何拼，才能使结果既不重复又不遗漏呢？

    生3：可以先固定一块三角板的一个角，然后用另一块三角板的角去拼.

    师：这位同学是从拼三角尺——“形”的角度来分析的. 那还有其他的方法吗？

    生4：可以将两块三角板的角度进行“加”或者“减”.

    设计意图对于活动1，学生通过对三角尺已有角的认识，激活了已有知识经验，为积累更高层次的活动经验做准备. 此阶段学生对角的认识是直观的、未经提炼的、与操作紧密相关的浅层次活动经验. 此时，教师可引导学生对已有经验进行观察、猜想、归纳和内化，形成较有条理的数学活动经验：①割补思想：“拼”与“叠”对应几何中的“补”与“割”. ②数形结合思想：“拼”与“叠”的过程对应着角度之间的“加”与“减”. ③拼角有两种方法：一种是从图形上来研究;另一种是从角度上来研究. “拼角”的本质是“拼角度”.

    2. 两副三角尺拼角：积累活动经验

    活动2的教学片段如下.

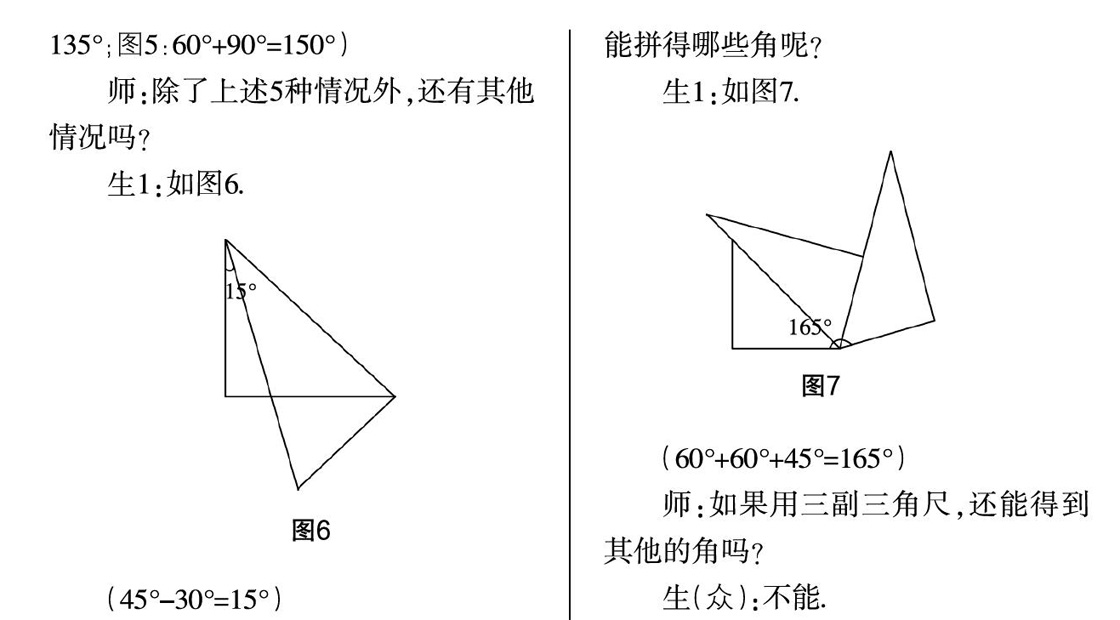
    师：接下来，用两副三角尺，我们还能拼得哪些角呢？

    生1：如图7.

    师：如果用三副三角尺，还能得到其他的角吗？

    生（众）：不能.

    师：观察三角尺所拼得的这些角，它们之间有何共同特点？

    生（众）：角度都是15°的整数倍.

    师：如果将15°作为一个模板，那么0°～180°之间15°的整数倍角都可以由此模板画出.

    设计意图学生在活动2中进行了思考、总结和内化，积累了相关的活动经验，但是系统的经验很难在一次操作过程中获得. 假如经历多次反复操作、探究过程，学生会对已有的活动经验进行再积累和完善，从而逐渐形成概括性的经验：①用两副三角尺拼角，还可以拼出一个新的角度——165°，但用三副或多副三角尺进行拼角，并不能拼得其他角度;②从结果上分析，发现拼得的角都具备共同的特征——均为15°的整数倍角，因此将15°作为模板能画出15°的整数倍角.

    3. 借助模板画角：迁移活動经验

    活动3的教学片段如下.

    数学活动经验的迁移能力是学生的一种创新能力，即在原有活动经验的基础上再次遇到类似的情景，将已有数学活动经验迁移应用于类似情景，产生新的认识经验，按照这种模式，重复使用这种经验，形成系统的经验. 活动3用含17°和19°的模板，通过活动经验的迁移，发现不仅能画出偶数角，还能画出奇数角. 此时，教师引导学生思考画出的角度和给定模板之间的关系，归纳出“15是30和45的最大公因数，1是17和19的最大公因数”. 由特殊情况推广到一般，即给定两个角的模板，求两个角的度数的最大公因数，以这个最大公因数的角度作为新的模板，可以画出其任意整数倍角，这个过程就是“经验迁移”的过程.

    4. 画角方案设计：升华活动经验

    活动4的教学片段如下.

    设计意图经历前面活动经验的激活、积累和迁移，活动4是对此前积累的活动经验的应用和升华. 如果给定m°和n°的模板，本质上是求这两个度数（m和n）的最大公因数，所画出的角就是这两个度数的最大公因数的整数倍角. 由此，如果给定3个角、4个角乃至多个角的模板，通过角度之间的加减与倍数关系，所能画得的角就是这些角的最大公因数的整数倍角. 教师通过引导，将学生已有的数学活动经验进行升华，长此以往，形成数学直观.

    1. 经历经验激活到经验升华，积累实践活动经验

    实践经验主要是从客观世界中抽象出来的，是通过动手操作从数学活动中获得经验，并将所获的相关经验应用于解决实际问题. 在整个活动过程中，学生根据已有对角的认知，激活了原有的经验. 学生还在反复操作活动过程中归纳、思考和内化，形成了概括性的经验，发现了三角尺拼角的一般规律. 教师则通过引导学生将已有活动经验迁移到类似的问题中，以解决模板画角问题，并对之前所获得的一般性规律进行推广和总结. 这种学习方式，不是让学生被动接受教科书上的现成结论，而是鼓励学生从自己已有的“数学经验”出发，变“听数学”为“做数学”，变“看演示”为“动手操作”，变“机械接受”为“主动探究”，培养学生的动手操作能力、解决问题的能力和创新精神，积累实践活动经验.

    2. 经历无序认识到有序认知，积累思维活动经验

    思维活动经验是将实际问题进行数学化和符号化，并在符号化的过程中积累活动经验. 从认识的过程来说，直观感受是在事物的作用下，学生在头脑中形成的感性知识. 尽管直观感受只能形成感性知识，但它却是思维的起点，是感性知识转化为理性认知的开端. 学生在本实验中已有的认识是三角尺本身具备的一些特征，此类经验很大一部分是数学活动现象或者直观结果，是比较粗糙、模糊和无序的认识，受个人的主观意识和活动情景影响比较大. 学生在思维层面通过思考，发现其实“拼角”就是在“拼角度”，“拼角”是操作层面的认识，而“拼角度”已经上升到了思维层面，角度的加减或者倍数关系是拼角的符号化表达. 因此，在用模板画角的过程中，从操作层面理解已经有所局限，此时需要从思维层面进行再认识，通过归纳总结得到结论. 学生在探究活动过程中从无序的结果入手，经过探究、思考、归纳和内化，形成思维上的有序认知，并积累思维活动经验.

    本节课从特殊入手，尝试探索、归纳一般规律或结论，借助演绎推理验证一般规律. 这个过程能让学生感悟数学基本活动经验积累的思维模式，长此以往，能形成数学直观，达到数学基本活动经验积累的最高层次.