化归，找到数学问题的本源

    任庆 史丹萍

    

    

    

    [摘? 要] 思想是数学学习的关键所在，也是核心素养之一，为此，我们在教学过程中要充分重视数学思想的渗透与引领，达到“授之以渔”的效果. 在初中数学的教学过程中，化归思想是数学思想的一种，笔者结合经典案例，具体阐述了化归思想在初中数学问题解决中的应用.

    [关键词] 思想;初中数学;化归;核心素养

    随着新课程改革的推进及促进学生数学素养教育理念的提出，数学思想的渗透在教学中越来越受到重视. 化归思想是数学思想中的一种重要思想，在数学问题的解决中起着重要的作用. 它是转化和归结的简称，即在问题解决的过程中寻找新知识与旧知识之间的联系，从而将一个问题化难为易，化繁为简，化复杂为简单. 笔者拜读了前辈与同仁们此前对它的研究，结合自身在教学实践中的反思与总结，认为化归思想在初中数学问题解决中的应用主要表现在以下几个方面.

    代数问题：化难为易

    化难为易是化归思想在数学问题解决中最基本的转化过程，是在解决较难问题时利用知识之间的内在联系，将其转化成简单问题，从而使问题得到解决的过程，该方法的优势在代数问题中尤为突出.

    上述例题如果不化归，则较为复杂，化归后则瞬间变得简单. 利用化归思想将难题转化为简单问题的基本方法是，充分挖掘问题的实质，找到该问题与已有知识在本质上的联系，从而将问题转化为容易解决的问题后再求解.

    边角问题：化斜为直

    “化斜为直”是针对三角形而言的，初中阶段对解斜三角形未做要求，因此遇到與斜三角形有关的问题时，可以将其化归为解直角三角形问题，其中求三角形中的边、角是常见的题型.

    “化斜为直”的实质是将线段的长度问题转化至直角三角形内，利用勾股定理和锐角三角函数来解决. 在这个过程中，找准目标三角形是关键，不破坏特殊角是注意点.

    求值问题：化数为形化数为形，即数形结合思想的运用. 将代数问题转化为几何问题，可以使问题变得更加直观、形象.

    在上述问题中，利用化归思想将代数求值问题化归为几何问题，在求解的过程中起到了关键作用，由此我们可以让学生体会到代数与几何的交融，感受到数学知识的整体性.

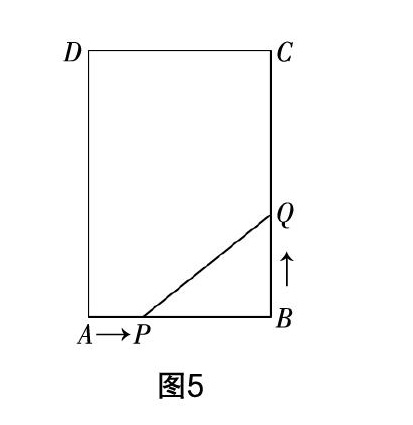
    动态问题：化动为静

    动态问题是初中数学中的常见问题，也是让学生感到颇为“头疼”的问题，其实初中阶段的动态问题并不会很深奥，通常都可以化归成静态问题来求解.

    上述两道例题，其实用到了化归中的不止一种方法，但是“化动为静”是解决动态问题的主要思想. 通过挖掘条件与分析问题，能让动点“静”下来，将问题简化.

    本文列举的化归思想方法是笔者在教学实践中使用频率较高的方法，当然，在数学思想中并不仅仅只有这几种. 我们要在实践中不断地思考，不断地深入研究问题，这样才能“解锁”更多的方法. 在教学中，笔者发现很多人认为化归思想与转化思想是相同的，其实它们的实质不尽相同，笼统地说，转化是找到不同问题之间的联系，而化归是找到复杂问题中隐含的基本模型与基本问题. 在解决问题的过程中，需要用化归思想中的哪一种方法并不是固定的，每种题型的方法也不是单一的，因此，在教学中教师应引导学生学习数学时学会灵活变通. 因为只有这样，才能看到问题的本质，找到问题的本源，将数学问题化难为易，化繁为简，轻松解决.