浅谈数学教学中类比思想的应用
魏育玲


[摘? 要] 类比推理教学在概念、性质、判定、解法策略等方面的运用能够更好地帮助学生记忆、掌握所学知识,不断激发学生数学学习的兴趣、开阔学生视野,在培养学生数学思维品质和能力的同时提升课堂教学的效率.
[关键词] 类比思想;概念;同构;属性
类比思想在知识繁多、概念定理纷繁复杂的数学学科中的应用能够有效促进教学效率的提升,能使学生在类比旧知识的过程中对新知识展开有效的探究. 承上启下的探究过程能使学生对新旧知识纵向、横向之间的内在联系获得更好的掌握,使学生在符合认知心理发展的学习中更好地掌握数学“四基”,同时实现数学能力的发展.
不过很多教师在应试教育的压力之下仍旧将追求学生的成绩视为最重要的目标,学生数学思维能力的培养却被大大忽视了,对类比思想的把握与理解因此很少落实于实际教学中.
概念类比
孤立地理解、记忆初中阶段所学的数学概念将会令知识孤立而缺乏联系与延伸,学生在长期孤立理解、记忆概念时将会把数学学习看成一种负担. 因此,教师应该对培养学生快速、准确掌握概念这一问题进行深入的思考,运用类比思想进行概念的教学以及概念的纵向延伸,使学生在集“点”串“线”的概念教学中不断触及概念的本质并获得更好的理解.
1. 问题引领下的概念类比
环环相扣的问题串能引领学生在新旧知识之间进行类比并获得新概念的理解,使学生的学习效果事半功倍.
案例教师在“分式”这一章的教学中,首先可以设计一定的生活情境并帮助学生得到代数式,然后再设计如下问题串引领学生探究:(1)刚刚得到的式子,,都是整式吗?(2)这些式子可有共同特征?(3)大家是否能从这些共同特征上联想到一些类似的知识呢?(4)结合已有知识及其共同特征是否可以给出其定义呢?(5)大家能回忆起小学阶段学习的相关知识吗?(6)大家猜猜看这些分式所涉及的知识吧. (7)大家觉得这些知识和分数的相关知识有关联吗?
由此可见,借鉴分数的相关知识进行类比、联想是能够对分式的性质、化简、运算等问题进行研究的.
设计问题串并引领学生对概念形成理解,能使学生在不断思考的状态中更加清晰而立体地掌握概念并使其感受到学习的趣味.
2. 经验延伸下的概念理解
顺应学生的旧知识经验并引导学生在反复比较和归纳中明确概念间的异同,能使新旧概念之间的衔接更加自然,并促进知识脉络在学生头脑中的清晰形成.
案例教师在相似三角形这一概念的引入教学中可以这样设计:事先准备好两个全等三角形和一个与之相似的三角形,取出两个全等三角形并设问:大家以为这两个三角形的形状、大小之间的关系怎样?存在这种关系的两个三角形应该怎么称呼?怎样定义全等三角形呢?取出另一个三角形再设问:大家觉得这个三角形和刚刚两个三角形在形状、大小上又存在着怎样的关系呢?它们之间可有相似的地方?第三个三角形又应该给它一个怎样的名称?对这些三角形之间所存在的关系进行定义又应该怎样描述呢?
笔者从学生已有知识和经验出发进行了多角度、多层次的问题设计,使学生在解决问题的过程中获得了知识的回顾以及新概念的形成,自然顺畅的设计令学生在问题的思考和探究中获得了知识、能力的同步提升.
同构类比
图形的衍变、通解的归纳这些知识的横向拓展能使学生学会更好地运用知识,因此,教师应该引导学生在数学结构上探寻知识间的相似性并进行同构类比、知识转化,使学生最终能够顺利拓宽知识并构建自然清晰的知识体系.
1. 图形同构
从图形的关系出发并进行图形的组合继而构成新图形,能使学生在思维的拓展、突破甚至超越中获得数学核心素养的发展.
案例勾股定理的复习教学中设计以下问题.
观察图形并回答问题.
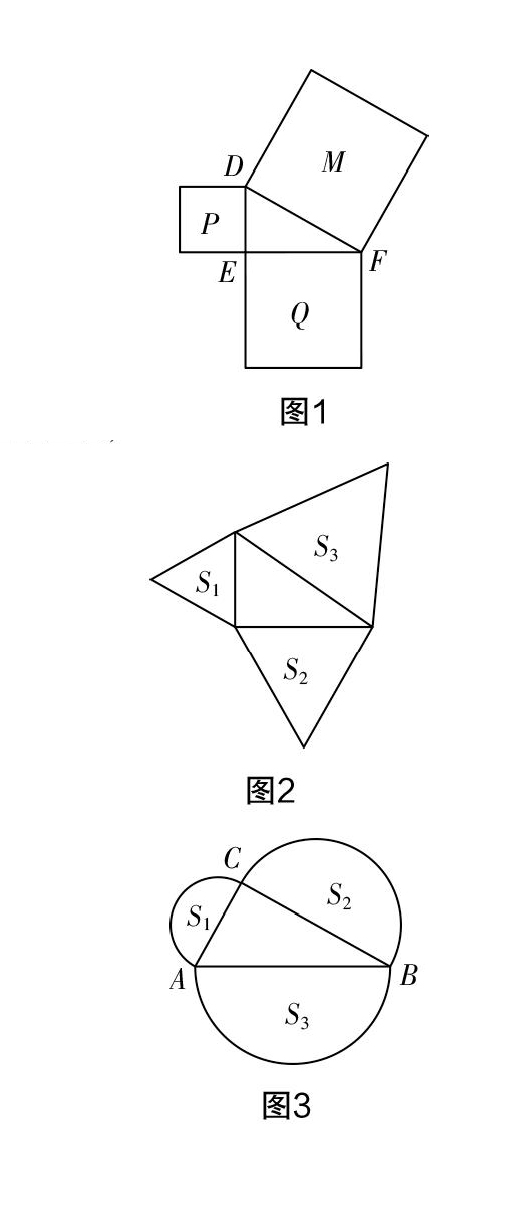
问题1:如图1,若△DEF是直角三角形,正方形P、Q的面积分别是9、15,则正方形M的面积应为______;
问题2:如图2,以直角三角形三边为边并向外作正三角形,则所得正三角形的面积S、S、S之间的关系为______;
问题3:如图3,以直角三角形三边为直径向外作半圆,则所得半圆的面积S、S、S之间的关系为______;
问题4:如图4,若直角三角形的直角边是3和4,以其三边为直径作半圆,则阴影部分面积为______.
勾股定理这一初中数学核心知识在解题中的应用是极为广泛的,教师引导学生在图形的同构类比中进行思考和探究,能使学生在渗透等积变换、数形结合思想的解题探索中获得空间形象思维的提升.
2. 解法同构
引导学生在千变万化的解题中发现规律以及它们的特征,能使学生在精心设计的解法同构的解题练习中学会猜想、探索和验证并最终寻得规律.
案例“握手问题”:n个人之间两两握手的次数一共有多少?
解:若第1个人分别和其他(n-1)个人握手共握手(n-1)次,第2个人分别和其他(n-1)个人握手也是(n-1)次……由此类推,第n个人和其他(n-1)个人握手也是(n-1)次,则有n×(n-1)次,此时每两个人之间握手的次数明显是2次,因此n个人之间两两握手的次数一共有n(n-1)次.
贴合学生生活的“握手”情境令学生兴致勃发,教师设计的这一模型也很好地锻炼了学生的归纳概括能力.
属性类比
引导学生进行空间、立体的感知并使其顺利构建知识的立体架构,能使学生在五花八门的知识梳理和问题解决中获得思维的提炼,也能使学生在知识的相同属性的类比中获得知识的深化与融合.
1. 个性类比
教师在某个知识或问题的教学之后往往会对其进行个性化的特殊处理,这种研究知识或问题特殊性的教学能使学生在层层深入、螺旋上升的教学中获得更加深刻的认知.
案例教师在“平行四边形”的教学中首先可以从其定义入手,然后引导学生在平行四边形边、角、对角线上进行其特点的研究并最终得其性质,然后再引导学生从特性上进一步学习如何判定平行四边形,最后再将矩形和菱形这两种特殊的平行四边形引入课堂,使学生在渗透类比思想的逐层教学中获得深层次的认知和理解. 逐层深入类比的教学也使学生更好地感受到了矩形定义的特殊性,新旧知识融会贯通的教学也令学生的知识、能力获得了螺旋形的发展.
2. 共性类比
教师应在如何促进学生的思考、感悟、思维上不断进行探索和追求,共性学习策略是教师在日常教学中应该重视并进行渗透的.
案例在“代数”的复习教学中可以按图5所示的代数思维路径进行提炼.
将代数的学习路径进行类比提炼可得图6所示的几何思维路径.
事实上,从共性學习的角度还可以类比、提炼出如图7的统计的思维路径.
教师在挖掘生活原型、问题抽象表述、建立模型、探索性质与运算、应用生活等一系列的教学中引导学生不断思考与探索,能使学生在构建新知、解决问题的过程中养成良好的思维习惯,数学思维的理性美也会因此得到很好的彰显.
类比推理教学在概念、性质、判定、解法策略等方面的运用能够更好地帮助学生记忆、掌握所学知识,使学生在探索新知、梳理知识、归纳题型、总结方法、提炼思维的过程中不断激发数学学习的兴趣,在不断开阔学生视野、培养学生数学思维品质和能力的同时还能提升课堂教学的效率.

