学好数学的必备知识

    蒋月兰 周小勇

    

    

    [摘? 要] 以几个定理为例的片段式学习不仅能让学生理解定义，而且能不断引导学生，让学生自己提出问题，接着根据他们所提出的问题来引导学生进入更深层次的学习. 通过这种方法可以不断地加强学生的逻辑思维能力，提高学生探究问题的趣味性.

    [关键词] 片段学习;提问;逻辑思维;自主学习;内角和

    在当前教学模式下，学生看到数学都会感到头疼，对数学没有什么兴趣，自然也就学不好，这是个很重要的“数学问题”. 那么如何才能提高学生学习数学的兴趣呢？其实身为一名教师，仅对概念、定理进行简单阐述是远远不够的，要让学生真正地自己去思考问题才是关键，要让学生自己带着问题去学习[1]. 让学生自己去咀嚼、自己去发现的自主学习更需要的是细心. 接下来，笔者列举几个片段来讲述如何学好数学.

    提问式，深层次学习，对于深入的问题有自己的思考

    老师问：数轴是什么？

    学生答：可以用一条直线上的点表示数，这条直线叫作数轴.

    不难看出，学生们看了书本之后，很容易得出数轴的概念，但是简单地去理解这个概念往往是不够的，老师在学生回答完之后可以进行下一步引导.

    老师：那我继续进行补充了. 既然是一条直线，直线上的点可以表示一个数，那么数轴上的点，数是随便取呢？还是有什么硬性规定？大家试着去解答一下.

    接着学生们进行了激烈的探讨，但是依旧没有很好的答案，老师继续引导.

    老师：看来同学们还是没有得到很好的答案，那我换个方式问一下. 原点是否可以随便取呢？还有数可以分为正数、负数，数轴上的点可以怎么来区分正负呢？这些该怎么解决呢？你们继续进行探讨.

    接下来，给予学生充分的时间思考讨论，不一会儿，就有人得出了结果.

    学生：我们可以任取一点表示“0”，这点我们就称之为原点. 那么，规定了原点之后就是原点左邊为负，右边为正.

    老师：很好，同学们经过逐步的学习思考，相信已经琢磨透了大部分，自己得出的答案可以让你们记得更牢.

    老师通过不断的引导，将学生逐渐引入更深层次的学习，同时教师设定的问题也是层层深入的，这样非常有助于学生思维的打开，从简到难，逐步加强. 之所以不直接给学生结论，目的就是让他们养成自我思考、自我发现问题、自我解决问题的能力.

    下面我们再通过另外一个例子对上述内容继续加以补充.

    在课堂开始的时候，老师通过生活中的例子来引入今天所要学习的内容.

    老师：同学们，在我们生活中，三角形应该是最常见的图形之一吧，那么你们知道三角形三个内角的和是多少度吗？

    这种问题自然是难不住学生的.

    同学们异口同声：三角形的内角之和为180度.

    老师：这是自然难不住大家的，既然我们都知道了三角形的内角和为180度，那么四边形、五边形、六边形的内角和为多少呢？大家可以进行讨论研究，想办法得出相关的答案.

    由三角形过渡到四边形、五边形等，由简到难地去推导，这样可以激发学生学习的兴趣，同时又不会因为难度较低或过难而让学生失去学习的积极性，同时也让学生学会触类旁通、举一反三的方法.

    学生：老师，我们可以通过用量角器来测出四边形、五边形的每一个内角的度数再来求和.

    老师：这样的解决问题的方法很好，但是你们有没有想过一旦变成了十边形、二十边形、n边形，还能测量得过来吗？还有没有什么更简单的方法可以让你们得出这个问题的答案呢？

    这个问题的设置，就是想让学生更好地去学习解决方法，让他们带着问题去研究. 学习是为了更好地掌握方法而不是蛮干.

    这个问题显然难住了学生，他们纷纷陷入了深深的思考.

    学生：老师，我们发现不管是四边形还是五边形都可以分割成几个三角形，这样就能解决问题了.

    老师：不管是几边形我们都可以分解成三角形来解决，这样不仅可以节约测量的时间，还能将我们所学习到的知识进行整合，以达到活学活用的目的.

    上面的过程中教师首先通过“三角形内角和”的例子来引入多边形的内角和，由易到难，学生如果想要真正去理解这个问题，一直用第一位学生所说的“死方法”是不行的，烦琐的操作和死脑筋是很难解决数学难题的. 学好数学的关键永远是学生的逻辑思维，这并不是一日养成的，通过自我探讨、自我提问、自我发现问题，才能得到很好地提高.

    要正确解题我们需要学很多的知识，要避免思维定式的影响，掌握更多的思维方法才是关键. 读题跟读书也有相似之处，正如古人所说：书读百遍，其义自见，读题也是这个道理. 我们要带着问题去读题，挖掘题中所隐含的条件，这些条件都是能帮助到解题的[2]. 永远不要为了解题而解题，那么做再多也无用，做一题就要做到有自己的“思维收藏”.

    认真读题，挖掘有用信息

    例1? 单项式-xmy2与5x3yn相加结果是单项式，那么m+n为多少？

    分析? 我们拿到这道题目的时候，不难看出题目中所给出的信息其实是很少的，我们要是盲目地将题目中的信息进行处理是不可能得出答案的，况且此题的条件很难进行处理. 碰到这种情况，我们不应该急着去解题，而是应该重新去读题. 不难发现，题目中有一个很重要的信息就是“仍为单项式”，这个条件的发现会让所有的问题都迎刃而解. 和为单项式其实就已经说出了答案，即x和y的指数分别为同样的数，即m=3，n=2. 所以说，好好审题永远是解题最关键的一步，磨刀不误砍柴工，完整清楚的审题会让解题效率更高.

    我们再看一下这个例子.

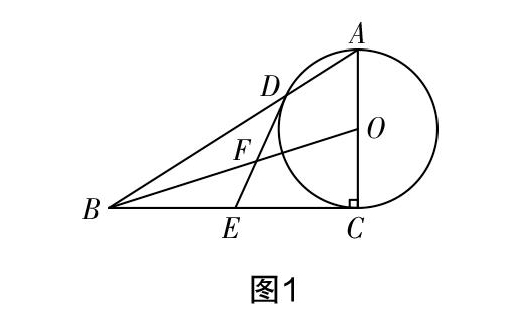
    例2? 如图1，在△ABC中，直线BC是圆O的切线，AC=4，BC=4，AC是圆的直径，E为BC的中点，直线OB与直线DE相交于点F，直线AB与圆相交于点D.

    这一题，老师并没有给出问题，而是让学生们来设计这道题的问题，还开了个玩笑：“要足够的难哦. ”

    学生自己出题，就需要学生对题目有着特别深的理解，再自己去发现问题.

    第一位学生发现，在Rt△ABC中，我们已知AC和BC的长，根据勾股定理，就很容易得出AB的长了. 所以他的问题是：求AB的长.

    很显然，这个问题很简单，只需简单的乘方运算，同学们也都不屑一顾.

    第二位同学提出了自己的看法，他的问题是：证明ED是圆O的切线.

    這个问题难度明显增加，证明题的难点在于切入点能否找到，当学生能找到正确的切入点，就能很迅速地解决问题，若不能，就好像无头苍蝇一样，找不到方向.

    过了一会儿，就有人得出了答案. 一个学生说到：证明切线的关键是垂直，所以连接OD，CD，因为AC为直径，则CD⊥AD，又已知AB，AC，BC的长，便可知道∠A=60°. 在△ADO中，因为AO，DO都是半径，所以二者是相等的，即△ADO为等边三角形，也可进一步知道△DOC为底角是30°的等腰三角形. 在△ADC中，AD，DC的长也可轻易得到，这样EC=DC就也得到了，△DEC便又是一个等边三角形，那么DE⊥DO便也得到了.

    老师：很好，这个问题相比上一题难度大了很多，考查了很多三角形以及圆的知识，较为系统和完整，是一个不错的问题. 那么还有其他同学有问题吗？

    显然，在第二个问题的解答过程中已经解决了很多学生的问题，比如，∠A的度数、AD的长等等. 过了许久，才有第三个问题.

    这位学生问道：连接OE，求BF ∶ FO.

    这个问题的难度又变大了一点，不仅仅局限于原题，而是在原题的基础上添加辅助线来提出问题. 此时学生们正感受着解题的乐趣，有不少人发现了解决的方法.

    不难发现，△DBF∽△EOF，所以BF ∶ FO也就是DB ∶ EO的比值，前面已经解出了AB和AD长，所以BD也是显而易见的，EC和OC也一样求了出来，所以EO的值也能得到，答案就显而易见了.

    通过上面的两个例子，笔者认为做题中切记不能盲目地解题，要多花时间来读题. 特别是第二个例子中让学生提出问题，学生需要多研究题目中给出的已知条件内容，其次还要将题目中的隐含条件给挖掘出来，一旦这样的条件被挖掘到，对于解题有很大的帮助.

    综上所述，学好数学绝非难事，也绝非易事. 它需要的不是广泛解题，不是解题阅历，而是思考. 这不是一个习惯，而是众多习惯，自主学习、自我发现问题、自我提问、良好的审题……都是必不可少的. 其中，笔者认为审题和自主发现问题是现阶段很重要的两个决定性因素，一个决定学生是否能进步，另一个决定学生是否能正确做题. 教学中教师应该注意学生相关意识与能力的培养.

    参考文献：

    [1]章建跃，林崇德.中学生数学学科自我监控能力的发展[J].中国教育学刊，2000（4）：47.

    [2]陆昌勤，周谦.问题解决的实验性研究——解代数应用题的认知结构[J].心理科学，1998（2）：262-263.

    作者简介：蒋月兰（1978-），本科学历，中学高级教师，从事初中数学教学工作，曾获扬州市优秀学校教科室主任，扬州市青年教师基本功大赛一等奖;周小勇（1979-），本科学历，中学一级教师，从事初中数学教学工作，曾获仪征市青年教师基本功大赛一等奖.