构建活动过程，让主动探究在心中落地生根

    张开良

    

    

    

    [摘? 要] 文章赏析了两节获得专家和教师高度评价的同课异构课程的教学片段，从中借鉴数学教学活动的设置方法，让数学活动起到应有的作用，避免在教学中开展毫无意义的“假活动”.

    [关键词] 数学活动;活动过程;主动探究;平均数

    数学教学活动是师生积极参与、交往互动、共同发展的过程. 有效的教学活动是“学”与“教”的完美统一，学生是学习的主体，而教师是学习的组织者、引导者与合作者，起到路标和桥梁的作用. 有效的教学活动设计更能激发学生的兴趣，调动学生的积极性，引发学生的数学思考，变被动学习为主动学习. 因此，数学活动的构建尤为重要，好的数学教学活动能激发学生求知欲，启数学之思，引探寻之路. 但是很多数学老师轻构建活动，重练习，轻知识的探究过程，重结论的记忆. 很多老师的活动过程都是假活动，如何让学生亲历问题的探究过程，体会面对数学问题时的思考方式、方法、路径和策略，体悟过程中的关键方法与核心思想，在探究过程中提升数学思维？笔者在教研活动中观摩“平均数（2）”两节同课异构的课，学生经历数学活动的探究过程，激发了主动探索，赢得了听课专家和教师的高度评价，现将这两节课的部分教学片段描述出来，与大家一起分享收获.

    1. 设置合理情境，让学习数学的必要性在感受中生成

    新课的引入要让学生充满好奇心、探究欲，虽然情境的引入有两种不同方法：从数学内部引入和从生活引入，但是不管选择哪一种，只要符合学生的认知水平和学习积极性的都是好情境. 如果能让学生感受学习数学的必要性，那么学生学习的动力会更强.

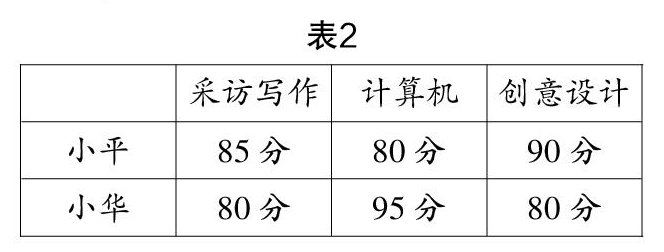
    片段一? 见表1.

    通过对比两个问题情境的引入，发现第一个问题情境比较僵硬，不自然，这样就不能更好地激发学生学习的兴趣，问题情境应该体现简洁、自然、适当，更应该精准. 第二个情境更直接，引发学生深度思考，调动学生的学习积极性，在知识的碰撞中，生成学习数学的种子. 让学生感受、体验学习本节内容的必要性和合理性，自然地引出加权平均数概念. 因此设置合理情境，能让学习数学的必要性在感受中生成.

    2. 设置恰当问题，让学习数学的积极性在尝试中收获

    这个环节的设计把问题抛给学生，让学生主动思考问题，根据广播站招聘的侧重点：对创意设计要求比较高，那么需要看中什么条件呢？学生很容易会根据侧重点，最终选择小平. 从数学知识层面来看，主要是为引出“权”的概念，这样设计问题面向全体学生，问题也具有一定的开放性，注重启发学生的思考，从而获得探究数学问题的初步经验.

    这个环节的设计依然是让学生先思考，如果我是电视台的台长，应该思考招聘的人员擅长什么，是采访写作、计算机还是创意设计呢？然后思考应该给出什么样的计算标准来录取相应的人. 答案可能是按照2 ∶ 3 ∶ 5这样的比例，或者是按照30%，25%，45%这样的百分比来确定需要的人员. 学生在尝试中，积累数学活动经验. 这样的问题设计能引导学生自主探索，在猜想、验证中，让学生去思考，促进学生对“权”的理解，不难发现权可以是不同的频数、不同比重、不同的百分比. 根据平均数的概念能顺利地推导出加权平均数的计算方法，这样的问题设计能让学生成为真正的学习主体. 这样设计问题具有一定的高度，更体现开放意识. 从具体到抽象，经历知识的获得过程，在这个过程中既培养了学生的观察能力、语言表达能力，还培养了学生的概括能力和思维能力.

    （2）问题解决要留痕，关注学生的思维过程.

    （1）若学生的成长素质发展报告书中数学平均成绩最终按1 ∶ 1 ∶ 1计算，那么哪个人的平均成绩最高？

    （2）若学生的成长素质发展报告书中数学平均成绩最终按1 ∶ 2 ∶ 5计算，那么哪个人的平均成绩最高？

    （3）若学生的成长素质发展报告书中数学平均成绩最终按30%，20%，50%计算，那么哪个人的平均成绩最高？

    （4）小明一学期的数学成绩如表5.

    （5）小明一学期的数学成绩如表6.

    片段四是另一个构建过程，从这个设计过程我们可以看出，对权的理解从特殊的比例1 ∶ 1 ∶ 1到1 ∶ 2 ∶ 5再到30%，20%，50%，最后到一般性的w ∶ w ∶ w，最终能推导出加权平均数的公式：= . 这个设计虽然开放性不强，但是我们可以看出这样的设计由浅入深，层次性很强，课堂教学注重找准已有知识的起点，让学生在已有知识结构的基础上经历数学知识的发生发展过程、亲历问题的探究过程. 关注学生的思维过程，让学生在探究的过程中渗透特殊到一般的数学思想，学生定会加深对知识的理解，定会让知识的理解在学生心中扎根.

    （3）问题解决要变式，关注学生的思维多样性.

    片段五? 为了调动学生学习数学的积极性，某校开展了数学知识竞赛活动，九（1）班派了15位同学参加比赛，共有三种得分：85分，80分，90分. 你认为添加什么条件就可以计算出平均分呢？追问：添加什么样的条件可以让平均分更高呢？

    这个例题设计的问题具有很强的开放性，学生可以添加很多条件. 方法一：可以给出85分、80分和90分的个数，例如个数为分别为：85分的个数为4个，80分的个数为5个，90分的个数为7个;方法二：给出85分、80分和90分所对应的比重，例如2 ∶ 3 ∶ 5;方法三：给出85分、80分和90分所对应的百分比，分别为20%，40%，40%. 老师可以继续追问还能以什么样的方式呈現呢？答案如图1、图2.

    对于本题的追问我们可以不断改变权的个数，减少80分的个数，增大90分的个数，或者减小80分的比重，变大90分的比重，这样都可以增加平均分. 可见这样设计问题虽然很简单，但是答案有很多种. 这样设计能让问题的答案具有多样性，所以能够启发学生去独立思考，发散学生的思维，更能提高学生对问题的深入理解. 虽然只有一道题，但是通过变式能够提高训练的效率，减轻学生的负担，促进学生多层次、多角度的探究，还能提升学生思考问题的能力，发散学生的思维，让学生的思维具有多样性，不断提高学生发现问题和提出问题、分析问题和解决问题的能力，同时培养学生的创新精神，激发学生的学习潜能，鼓励学生大胆创新与实践.

    3. 设置有效作业，在巩固中提升技能

    1.某校规定，学生的数学成绩由三部分组成：平时占15%，期中占20%，期末占65%. 小颖平时成绩80分，期中成绩85分，期末成绩90分.

    （1）小颖数学成绩的平均分是多少？

    （2）若小颖要使数学成绩的平均分达到90分，那么她在期末考试中至少要考多少分？

    2. 一家公司对A，B，C三名应聘者进行了创新、综合知识和语言三项素质测试，他们的成绩如表7所示.

    [ A B C 创新 92 85 67 综合知识 50 74 60 语言 88 45 67 ][表7]

    （1）如果根据三项测试的平均成绩确定录用人选，你选谁？

    （2）根据实际需要，广告公司给出了选人标准：将创新、综合知识和语言三项测试得分按4 ∶ 3 ∶ 1的比例确定各人的测试成绩，你选谁？

    这个设计的第一道题是巩固加权平均数计算方法，第二道题难度有所提升. 一方面能让学生感受到权的不同，平均分的分数就不同，两道题的重点是通过解题让同学们分清两种不同平均数的不同计算方法，以及不同的意义. 我们知道基本技能的形成需要一定量的训练，但要适度，不能依赖机械的重复操作，要注重实效. 教师应把握技能形成的阶段性，根据内容要求和学生的实际，分层次进行. 训练新知识，最重要的是建立在旧知识之上，奥贝尔（D·P·Ausubel）曾指出：“影响学习的最重要的因素，是学生已经知道了什么，根据学生的原有状况进行教学. ”教师要在原有知识上提出问题，引起学生思考，产生疑问，从而激发学生的求知欲. 所谓“学起于思，思源于疑”，在这个过程中，当堂巩固练习是架设在新旧知识之间的桥梁. 只有这样学生才能更深刻地领会基本的原理和概念，适当的训练巩固是必要的，这样学生不仅能掌握知识还能举一反三、触类旁通.

    学生是学习的主体，数学教学的载体就是数学活动，无论对学生掌握知识还是发展能力都是至关重要的. 在平时的教学中，一定要让学生感悟知识生长的过程，在活动中理解概念、法则;在活动中发展学生思维，渗透思想;在活动中提升学生的解题能力，深化知识的理解，让数学知识和能力在数学活动中自然落地生长，让我们的数学教学为学生的成长助力！