数学解题关键环节的确定与教学设计
张昆 罗增儒


【摘 要】 ?数学解题教学设计的一般程序分为三个部分:教师针对某个数学问题尽可能多地获得解决的思路;确定解题过程的关键环节;依据学生发生解题认识的心理环节及其过渡性中介,经由选择教学法的加工,设计具体的解题教学流程.教师悉心地完成上述三个互相关联的步骤,在课堂上依据学生具体的生成情况,加以适当的调整,就会最大限度地提高解题教学的有效性,保质保量地完成数学解题教学任务.
【关键词】 ?数学解题;解题教学:教学设计;关键环节
从某种程度上可以说,数学教学设计的过程就是将作为学术形态的数学知识转化为教学形态的数学知识的过程.数学教学设计是一项结构性的整体工程,它的构成要素主要体现在互相关联的三个侧面:理解所要传授的具体数学知识结构所呈现的环节及其联结中介的可能组成序列(简称“教材分析”);把握学生萌发数学知识(环节及其联结中介)的心理环节(呈现的是观念形态)及其过渡性中介(简称“学情分析”);通过创造性工作找到沟通这两种组成环节及其联结(或过渡性)中介的切合点(简称“教学法分析”).由此教师可以设计出合适的数学教学过程(如图1) [1].那么,如何依据学生发生数学知识的心理环节及其过渡性中介进行数学解题教学设计呢?
1 教师获得问题解决的巧妙思路
在数学解题教学中,与学生相比,我们教师具有强大的数学现实,通过深入思考,往往会发现非常巧妙的解决问题的逻辑思路,此时,如果教师直白地将这种逻辑思路直接地“下载”给学生,就会造成数学解题活动教育价值的极大损失.因此,好的数学解题教学设计在于教师想方设法将这种逻辑过程转化为学生发现解题思路的心理过程,也就是将形成解题过程的逻辑环节及其联结中介转化为学生萌生这一思路的心理环节及其过渡性中介,使这一思路逻辑过程的环节及其联结中介仿佛是学生从他自己心灵深处发生的.这是数学解题教学设计的真正要紧的地方,教师的努力也需要围绕着这一转化过程展开.我们看一个具体解题教学的例子.
例1 (2010年全国高考湖北卷理科题22) 已知函数f(x)=ax+ b x +c(a>0)的图象在点 1,f(1) 处的切线方程为y=x-1.
(Ⅰ)用a表示出b,c;
(Ⅱ)若f(x)≥lnx在 1,+SymboleB@ 上恒成立,求a的取值范围;
(Ⅲ)证明:1+ 1 2 + 1 3 +…+ 1 n >ln 1+n + n 2 n+1?? n≥1 .
分析 请读者自行寻找结论(Ⅰ)为:b=a-1,c=1-2a;结论(Ⅱ)为:a∈? 1 2 ,+SymboleB@ .
关于问题(Ⅲ),笔者通过长时间的思考,發现了一条巧妙思路:记1+ 1 2 + 1 3 +…+ 1 n > ln 1+n + n 2 n+1?? n≥1 为不等式①,仔细审视不等式①,发现这个不等式左边的形式可以记为1+ 1 2 + 1 3 +…+ 1 n =∑ n ?k=1 ?1 k ②.
由于ln n+1 =∑ n ?k=1 ?ln k+1 -lnk ③, n 2 n+1? =∑ n ?k=1 ??1 2k - 1 2 k+1?? ④,由③、④相加,知ln n+1 + n 2 n+1? =∑ n ?k=1 ?[lnk+1-lnk]+? 1 2k - 1 2 k+1??? ⑤.于是,仔细观察比较①、②与⑤的具体特点,知只要证明 1 k >ln k+1 -lnk+ 1 2k - 1 2 k+1? ⑥,对于⑥进行移项、合并同类项,知等价于证明 1 2k + 1 2 k+1? >ln 1+ 1 k? ⑦就达到了目的.
对于函数f(x)=ax+ b x +c(a>0),且b=a-1,c=1-2a,又且当a∈? 1 2 ,+SymboleB@ 时,f(x)≥lnx在 1,+SymboleB@ 上恒成立,并且不难得到当x>1时,f(x)>lnx.取a= 1 2 ,当x>1时,则有 x 2 - 1 2x >lnx⑧.在⑧中,取x= k+1 k? ,知 k+1 2k - k 2 k+1? >ln 1+ 1 k?? ⑨.比较不等式⑦与⑨,只要证明 k+1 2k - k 2 k+1? ≥ 1 2k + 1 2 k+1? 就行了.对此,我们不难通过计算,得 k+1 2k - k 2 k+1? = 1 2k + 1 2 k+1? ,从而由⑨成立得到⑦成立.
这道题的思路我们已经找到了,这条思路不同于当年高考命题者所提供的参考答案,计算简洁,方法优雅,具有较好的创新性.如果将这种答案不加以教学法的加工与处理,而直接“交给”学生,那就将会失去数学解题过程的很多促进学生思维品质、数学能力发生与发展的教学价值,也不会帮助学生在解题中生成有用的数学观念,及欣赏解题过程中的数学美感.为了更好地发挥数学解题教学的价值,我们应该首先从解答过程确定促进学生诸多心理品质发生与发展的关键环节,然后,再考虑对此进行教学设计.
2 数学解题思路中的关键环节的确定
众所周知,数学问题解题的过程,就是建立题设条件之间的联系而构成问题结论的过程,在解题过程中,题设条件与结论之间的贯通是由学生已经掌握了前在的数学知识作为桥梁的 [2].依据这种视角来看,仿佛是解题者前在的数学知识解决了问题(数学问题、或者生活中的问题),但是,问题的本质不是这样的,其中,我们必须看到:
其一,这种前在的数学知识是相对而言的,作为人类的数学知识与作为个体的数学知识,在解决问题时起着不同的作用.在数学解题教学过程中,教师是人类数学知识的代言人,教师将可以解决的数学问题或利用数学知识解决的生活中的问题,转化为培养学生相关心理品质的资源与力量.因此,在数学解题教学的过程中,数学教师需要首先帮助学生掌握解决某个问题所需要的知识,因为,如果学生目前的认知结构中还不具有如此的数学知识,他是不可能解决这一数学问题的.我们设想对于学生而言,这在教科书中所出现的数学问题,或者数学高考题,一般情况下通过课程的安排,学生已经掌握了这样的数学知识,至于针对某學生个体的特殊情况,需要具体的教授这个学生的教师单独考虑.
其二,只具有解决某个问题的数学知识还是不能解决问题的,因为,虽然是数学知识架设起从题设条件到问题结论的桥梁,但是,作为人类的数学知识如果不与学生个体相结合,那么,对于学生而言,这种知识还是客观的,不能为他所用,他还依然不能解决问题.人类的数学知识只有与具体个体的意识结构相结合,这才是属于具体个体的数学知识,这种数学知识对于这个个体才是有效的,才能支配知识去分析问题与解决问题.
其三,虽然个体拥有解决某问题的数学知识,但是在将这种数学知识运用到具体问题中的过程中,这一知识总是被个体征调的,形成知识运动的动力来源于个体思维活动的能动性,就是说,解题时,知识是僵死不动的,总是被个体支配的,问题解决的关键性环节就是在调整、调动与整合问题题设条件,知识要在这些题设条件的应用中得其所置,这种个体在问题题设的适当位置中安置知识的过程,必须由个体的思维能动性作用才能实现,它需要在个性化的数学观念的指令下,才能实现.
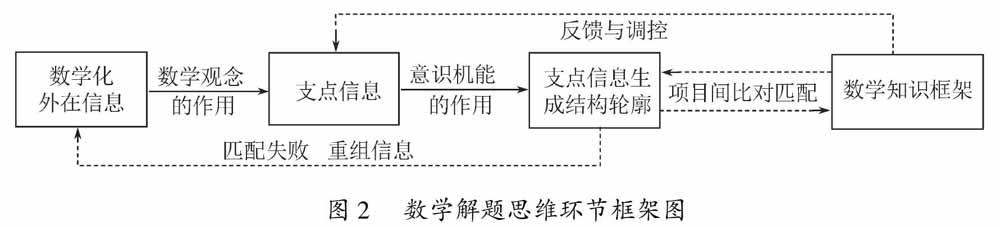
其四,发现决定问题的本质结构,从而利用数学知识获得解决问题思路的过程,就在于从作为题设条件的外在信息中选择并确定出支点信息.这种选择的过程又是外在信息与已经内化、并保存在意识结构中的数学知识之间的互相吸引,相互诱导,相互调整,从而实现数学知识对基于支点信息、并在支点信息“凝聚核”的作用下,将外在诸多信息进行结构化的信息封装过程,如图2所示.在这一整套的发现思路及采取行动验证发现的过程中,数学观念起着关键性的作用.
[JZ] 图2 数学解题思维环节框架图
其五,由于个体产生解决问题的行动不是无缘无故的,也不是盲目试误的过程,而是思维活动通过图2所示的一整套探究过程,对题设条件外在信息与个体已经掌握的数学知识之间进行酝酿,从而萌生了某些数学观念,个体解决问题的行动就是在这些(通过竞争,选择出的主导性的)数学观念指导下进行的.正是数学观念的作用,既可以调动外在问题的题设条件的信息,又可以调动内在解题数学知识,从而可以将这两者关联起来解决问题.
如此分析,我们可以确定解题教学的关键环节就在于个体如何取得指导操作题设条件行动的数学观念(一种指令).长期数学解题与教学经验使我们认识到,学生在习得数学知识的同时,总是在萌生数学观念,这其中有些数学观念由于经常使用,在解决问题时,个体可以信手拈来,不需要在新出现的问题背景的现场中即兴萌发了,而是成了某种自觉的行为,当此之时,在教师的教学中,就不构成解题教学的关键环节;而某些决定问题本质的数学观念在搜索解题思路中却不是轻而易举地可以得到的,此时,教师在解题教学设计时必须帮助学生现场萌生这种数学观念 [3].这就构成了解题教学设计的关键环节,确定解题教学设计关键环节的依据也就由此而生.
3 数学解题关键环节教学设计的构想与行动
就本例而言,教师设计这道解题教学的过程可以划分为如下几个环节:首先,从教师自己所定位的解题思路中确定关键环节(通过前面的分析,我们已经做到了);其次,追踪获得问题思路时处理关键环节的数学观念的源头;再次,揣摩并模拟学生萌生处理关键环节指令的心理活动过程 [4].针对例1我们所获得的思路而言,教师依次确定教学设计的关键环节在于两个“数学观念”的形成:(1)由(Ⅰ)、(Ⅱ)两问所建立起来的不等式⑧将要应用到第(Ⅲ)问的不等式①中;(2)由②作为基础,经由③、④而获得等式⑤,我们不妨称之为“求繁”的数学观念,事实上,它是在不等号(等号)所连接的两个式子应该具有“对等”的结构,或者更进一步地说,是在学生关于数学“对称美”的审美意向作用下而萌生的“对等”结构而建立起来的“求繁”的数学观念.
对于(1)中的这种数学观念,学生通过长期解答数学题,已经有了很深刻的体验,因而,它是比较容易发生的,于是,在教学设计时,渗透这种具体的数学观念就不作为非常重要的教学目标了;对“求繁”的数学观念在解题思路的发现中起着指导技术性操作的指令作用,然而,在学生的数学现实中,这项数学观念确是比较难以萌生的,原因在于求简是数学解题思维的主旋律,它的逆向性思维“求繁”受到思维定势的影响,却不容易产生了,因此,本例的教学设计就是要围绕着针对“求繁”的数学观念展开.关于这种“求繁”的数学观念的萌生,有时是经过长期的酝酿而形成的灵感的闪现,这种灵感的过程就连心理学家也难以说清楚,教师对学生解题时心理的起承转合的行为产生的心理环节过程也是难以清楚揣摩到的.
可以说,这些构成了教师设计数学解题教学的创造性能力的非常重要的一项教学目标,渗透“求繁”的数学观念就是解决这道题的最为关键的价值所在.如果数学教师在设计数学解题教学时心中不能对学生探究问题思路过程的那种深陷重围的痛楚,举步维艰的困惑,欲行又止的困局切体的理解,那就很难急学生之所急,想学生之所想.教师就必然会只满足于自己的讲清楚,如此,学生很难举一反三.因此,教师不仅要理解学生的知识基础,还要了解他们的思维方式与认识特点,基于此,把解题思路获得的曲折的思维过程作必要的设计,不只是讲教师加工整理好了的思维捷径 [5].笔者在带领学生解决这道题的教学时,就是围绕着渗透“求繁”的数学观念而展开,下面是笔者课堂教学的实录:
师:要证明不等式1+ 1 2 + 1 3 +…+ 1 n >ln 1+n + n 2 n+1?? n≥1 ①成立,大家有什么想法?
生1:如果获得不等式左边的前n项和的一个表达式,对问题的解决会带来很多好处,可是,我经过试探,很难找到这样的一个表达式(作为教师的笔者心理非常清楚,不等式①的左边是一个发散数列).
师:生1的这种想法,虽然在技术上我们难以得到执行,但是,我们可以分析生1想法的来源.他可能是这样想的:对于“不等号”(“等号”)也是一样,它们所连接的两边具有一种对等关系,他发现不等式①的这种形式不是对等的,加之以在“求简”的数学观念指令下,想到了求不等式①左边的一个表达式.可惜,我们办不到.怎么办?
生2:我们可以倒着想,既然①的左边的代数式不能直接相加得到一个结果,从而得到一个与①的右端形成一个“对等”的形式,那么,我想把①的右边转化为一个n项和的形式,如此也就形成了不等号的左右两边的“对等”形式了.但是,具体如何实现,我没有想好.
师:大家试探生2同学的这种观念是否可以实现?
说明,正如研究者分析中所产生的,在生2形成的观念的指令下,同学们找到了等式③、④,经由③、④又获得等式⑤,于是,要证明①成立,只要证明 1 2k + 1 2 k+1? >ln 1+ 1 k? ⑦成立就行了.
师:如何证明不等式⑦成立呢?
生3:第(Ⅱ)问提供的不等式肯定会起作用了.
说明:生3完整地给出了不等式①证明的思路.见解答的过程.
这种教学设计,数学教师对生1发生的数学观念的解释,揭示萌生“对等”的数学观念的过程是非常重要的,正是学生萌发出了这一数学观念的指令,形成了生2的处理这道题关键环节的技术性手段——萌生了“求繁”的数学观念.这个关键环节必须通过教师教学设计促使学生自己从自己的意识结构中生发出来,而不能“下载”给学生.这是实现数学解题教学的教育价值的最为重要的地方.
4 数学解题教学设计的一般程序
由这个例子我们可以归纳数学解题教学设计的一般程序:(1)教师针对某个数学问题尽可能多的获得解决的思路,教师最好的获得思路的方式是自己解题,因为,基于自己解题得到的思路,他会对自己的思路活动过程了如指掌,容易把握萌生某些数学观念的来源,从而容易发现解决问题的关键环节,教师抄别人解答的结果,就不可能对解题思路发现的过程具有如此深刻的体会;(2)确定解题过程的关键环节.解题过程的关键环节的主要标识就是指令问题思路中某些疑难步骤的数学观念是如何萌生的,这些基本上都是学生难以发生合适的数学观念的地方,它形成了培养学生创新能力的最佳资源;(3)依据学生发生数学知识的心理环节及其过渡性中介,经由选择教学法的加工,设计具体的解题教学流程.
5 简要结语
一位数学教师如果没有数学解题能力,他一定不可能成为非常优秀的数学教师;一位数学教学即使具有非常好的解题能力,他也未必一定能成为非常优秀的数学教师.数学解题能力构成了优秀数学教师的一项非常重要的必要条件,另一个非常重要的必要条件就是数学教师必须具备将解题能力转化为他的教学能力,对此,他需要特别关注学生发生数学问题思路的某些关键环节时学生的心理环节及其过渡性中介生成,从而设计教学过程循循善诱,引导学生依靠自己的认知结构的力量,重新萌生这种思路的关键环节,而不是将教师自己所得到的结果和盘托出地“下载”给学生,这其中,帮助学生萌生数学观念是数学教师在设计解题教学时需要特别注意的问题.对此,我们数学教师要思之再思,慎之 又慎.
参考文献
[1] 张昆,曹一鸣.完善数学教师教学行为的实现途径[J].数学教育学报,2015,23(1):33-37.
[2] 张昆,张乃达. 集中条件:数学解题的关键——教学设计的视角[J]. 中学数学(高中版),2016(2):9-12.
[3] ?张昆,罗增儒. 数學解题教学设计研究——指向渗透数学观念的视点[J]. 中学数学杂志,2017(11):15-18.
[4] 张乃达,过伯祥.张乃达数学教育——从思维到文化[M].济南:山东教育出版社,2007:186.
[5] 张昆.怎样备好数学课[J].中学教研(数学),1998(12):4.



【摘 要】 ?数学解题教学设计的一般程序分为三个部分:教师针对某个数学问题尽可能多地获得解决的思路;确定解题过程的关键环节;依据学生发生解题认识的心理环节及其过渡性中介,经由选择教学法的加工,设计具体的解题教学流程.教师悉心地完成上述三个互相关联的步骤,在课堂上依据学生具体的生成情况,加以适当的调整,就会最大限度地提高解题教学的有效性,保质保量地完成数学解题教学任务.
【关键词】 ?数学解题;解题教学:教学设计;关键环节
从某种程度上可以说,数学教学设计的过程就是将作为学术形态的数学知识转化为教学形态的数学知识的过程.数学教学设计是一项结构性的整体工程,它的构成要素主要体现在互相关联的三个侧面:理解所要传授的具体数学知识结构所呈现的环节及其联结中介的可能组成序列(简称“教材分析”);把握学生萌发数学知识(环节及其联结中介)的心理环节(呈现的是观念形态)及其过渡性中介(简称“学情分析”);通过创造性工作找到沟通这两种组成环节及其联结(或过渡性)中介的切合点(简称“教学法分析”).由此教师可以设计出合适的数学教学过程(如图1) [1].那么,如何依据学生发生数学知识的心理环节及其过渡性中介进行数学解题教学设计呢?
1 教师获得问题解决的巧妙思路
在数学解题教学中,与学生相比,我们教师具有强大的数学现实,通过深入思考,往往会发现非常巧妙的解决问题的逻辑思路,此时,如果教师直白地将这种逻辑思路直接地“下载”给学生,就会造成数学解题活动教育价值的极大损失.因此,好的数学解题教学设计在于教师想方设法将这种逻辑过程转化为学生发现解题思路的心理过程,也就是将形成解题过程的逻辑环节及其联结中介转化为学生萌生这一思路的心理环节及其过渡性中介,使这一思路逻辑过程的环节及其联结中介仿佛是学生从他自己心灵深处发生的.这是数学解题教学设计的真正要紧的地方,教师的努力也需要围绕着这一转化过程展开.我们看一个具体解题教学的例子.
例1 (2010年全国高考湖北卷理科题22) 已知函数f(x)=ax+ b x +c(a>0)的图象在点 1,f(1) 处的切线方程为y=x-1.
(Ⅰ)用a表示出b,c;
(Ⅱ)若f(x)≥lnx在 1,+SymboleB@ 上恒成立,求a的取值范围;
(Ⅲ)证明:1+ 1 2 + 1 3 +…+ 1 n >ln 1+n + n 2 n+1?? n≥1 .
分析 请读者自行寻找结论(Ⅰ)为:b=a-1,c=1-2a;结论(Ⅱ)为:a∈? 1 2 ,+SymboleB@ .
关于问题(Ⅲ),笔者通过长时间的思考,發现了一条巧妙思路:记1+ 1 2 + 1 3 +…+ 1 n > ln 1+n + n 2 n+1?? n≥1 为不等式①,仔细审视不等式①,发现这个不等式左边的形式可以记为1+ 1 2 + 1 3 +…+ 1 n =∑ n ?k=1 ?1 k ②.
由于ln n+1 =∑ n ?k=1 ?ln k+1 -lnk ③, n 2 n+1? =∑ n ?k=1 ??1 2k - 1 2 k+1?? ④,由③、④相加,知ln n+1 + n 2 n+1? =∑ n ?k=1 ?[lnk+1-lnk]+? 1 2k - 1 2 k+1??? ⑤.于是,仔细观察比较①、②与⑤的具体特点,知只要证明 1 k >ln k+1 -lnk+ 1 2k - 1 2 k+1? ⑥,对于⑥进行移项、合并同类项,知等价于证明 1 2k + 1 2 k+1? >ln 1+ 1 k? ⑦就达到了目的.
对于函数f(x)=ax+ b x +c(a>0),且b=a-1,c=1-2a,又且当a∈? 1 2 ,+SymboleB@ 时,f(x)≥lnx在 1,+SymboleB@ 上恒成立,并且不难得到当x>1时,f(x)>lnx.取a= 1 2 ,当x>1时,则有 x 2 - 1 2x >lnx⑧.在⑧中,取x= k+1 k? ,知 k+1 2k - k 2 k+1? >ln 1+ 1 k?? ⑨.比较不等式⑦与⑨,只要证明 k+1 2k - k 2 k+1? ≥ 1 2k + 1 2 k+1? 就行了.对此,我们不难通过计算,得 k+1 2k - k 2 k+1? = 1 2k + 1 2 k+1? ,从而由⑨成立得到⑦成立.
这道题的思路我们已经找到了,这条思路不同于当年高考命题者所提供的参考答案,计算简洁,方法优雅,具有较好的创新性.如果将这种答案不加以教学法的加工与处理,而直接“交给”学生,那就将会失去数学解题过程的很多促进学生思维品质、数学能力发生与发展的教学价值,也不会帮助学生在解题中生成有用的数学观念,及欣赏解题过程中的数学美感.为了更好地发挥数学解题教学的价值,我们应该首先从解答过程确定促进学生诸多心理品质发生与发展的关键环节,然后,再考虑对此进行教学设计.
2 数学解题思路中的关键环节的确定
众所周知,数学问题解题的过程,就是建立题设条件之间的联系而构成问题结论的过程,在解题过程中,题设条件与结论之间的贯通是由学生已经掌握了前在的数学知识作为桥梁的 [2].依据这种视角来看,仿佛是解题者前在的数学知识解决了问题(数学问题、或者生活中的问题),但是,问题的本质不是这样的,其中,我们必须看到:
其一,这种前在的数学知识是相对而言的,作为人类的数学知识与作为个体的数学知识,在解决问题时起着不同的作用.在数学解题教学过程中,教师是人类数学知识的代言人,教师将可以解决的数学问题或利用数学知识解决的生活中的问题,转化为培养学生相关心理品质的资源与力量.因此,在数学解题教学的过程中,数学教师需要首先帮助学生掌握解决某个问题所需要的知识,因为,如果学生目前的认知结构中还不具有如此的数学知识,他是不可能解决这一数学问题的.我们设想对于学生而言,这在教科书中所出现的数学问题,或者数学高考题,一般情况下通过课程的安排,学生已经掌握了这样的数学知识,至于针对某學生个体的特殊情况,需要具体的教授这个学生的教师单独考虑.
其二,只具有解决某个问题的数学知识还是不能解决问题的,因为,虽然是数学知识架设起从题设条件到问题结论的桥梁,但是,作为人类的数学知识如果不与学生个体相结合,那么,对于学生而言,这种知识还是客观的,不能为他所用,他还依然不能解决问题.人类的数学知识只有与具体个体的意识结构相结合,这才是属于具体个体的数学知识,这种数学知识对于这个个体才是有效的,才能支配知识去分析问题与解决问题.
其三,虽然个体拥有解决某问题的数学知识,但是在将这种数学知识运用到具体问题中的过程中,这一知识总是被个体征调的,形成知识运动的动力来源于个体思维活动的能动性,就是说,解题时,知识是僵死不动的,总是被个体支配的,问题解决的关键性环节就是在调整、调动与整合问题题设条件,知识要在这些题设条件的应用中得其所置,这种个体在问题题设的适当位置中安置知识的过程,必须由个体的思维能动性作用才能实现,它需要在个性化的数学观念的指令下,才能实现.
其四,发现决定问题的本质结构,从而利用数学知识获得解决问题思路的过程,就在于从作为题设条件的外在信息中选择并确定出支点信息.这种选择的过程又是外在信息与已经内化、并保存在意识结构中的数学知识之间的互相吸引,相互诱导,相互调整,从而实现数学知识对基于支点信息、并在支点信息“凝聚核”的作用下,将外在诸多信息进行结构化的信息封装过程,如图2所示.在这一整套的发现思路及采取行动验证发现的过程中,数学观念起着关键性的作用.
[JZ] 图2 数学解题思维环节框架图
其五,由于个体产生解决问题的行动不是无缘无故的,也不是盲目试误的过程,而是思维活动通过图2所示的一整套探究过程,对题设条件外在信息与个体已经掌握的数学知识之间进行酝酿,从而萌生了某些数学观念,个体解决问题的行动就是在这些(通过竞争,选择出的主导性的)数学观念指导下进行的.正是数学观念的作用,既可以调动外在问题的题设条件的信息,又可以调动内在解题数学知识,从而可以将这两者关联起来解决问题.
如此分析,我们可以确定解题教学的关键环节就在于个体如何取得指导操作题设条件行动的数学观念(一种指令).长期数学解题与教学经验使我们认识到,学生在习得数学知识的同时,总是在萌生数学观念,这其中有些数学观念由于经常使用,在解决问题时,个体可以信手拈来,不需要在新出现的问题背景的现场中即兴萌发了,而是成了某种自觉的行为,当此之时,在教师的教学中,就不构成解题教学的关键环节;而某些决定问题本质的数学观念在搜索解题思路中却不是轻而易举地可以得到的,此时,教师在解题教学设计时必须帮助学生现场萌生这种数学观念 [3].这就构成了解题教学设计的关键环节,确定解题教学设计关键环节的依据也就由此而生.
3 数学解题关键环节教学设计的构想与行动
就本例而言,教师设计这道解题教学的过程可以划分为如下几个环节:首先,从教师自己所定位的解题思路中确定关键环节(通过前面的分析,我们已经做到了);其次,追踪获得问题思路时处理关键环节的数学观念的源头;再次,揣摩并模拟学生萌生处理关键环节指令的心理活动过程 [4].针对例1我们所获得的思路而言,教师依次确定教学设计的关键环节在于两个“数学观念”的形成:(1)由(Ⅰ)、(Ⅱ)两问所建立起来的不等式⑧将要应用到第(Ⅲ)问的不等式①中;(2)由②作为基础,经由③、④而获得等式⑤,我们不妨称之为“求繁”的数学观念,事实上,它是在不等号(等号)所连接的两个式子应该具有“对等”的结构,或者更进一步地说,是在学生关于数学“对称美”的审美意向作用下而萌生的“对等”结构而建立起来的“求繁”的数学观念.
对于(1)中的这种数学观念,学生通过长期解答数学题,已经有了很深刻的体验,因而,它是比较容易发生的,于是,在教学设计时,渗透这种具体的数学观念就不作为非常重要的教学目标了;对“求繁”的数学观念在解题思路的发现中起着指导技术性操作的指令作用,然而,在学生的数学现实中,这项数学观念确是比较难以萌生的,原因在于求简是数学解题思维的主旋律,它的逆向性思维“求繁”受到思维定势的影响,却不容易产生了,因此,本例的教学设计就是要围绕着针对“求繁”的数学观念展开.关于这种“求繁”的数学观念的萌生,有时是经过长期的酝酿而形成的灵感的闪现,这种灵感的过程就连心理学家也难以说清楚,教师对学生解题时心理的起承转合的行为产生的心理环节过程也是难以清楚揣摩到的.
可以说,这些构成了教师设计数学解题教学的创造性能力的非常重要的一项教学目标,渗透“求繁”的数学观念就是解决这道题的最为关键的价值所在.如果数学教师在设计数学解题教学时心中不能对学生探究问题思路过程的那种深陷重围的痛楚,举步维艰的困惑,欲行又止的困局切体的理解,那就很难急学生之所急,想学生之所想.教师就必然会只满足于自己的讲清楚,如此,学生很难举一反三.因此,教师不仅要理解学生的知识基础,还要了解他们的思维方式与认识特点,基于此,把解题思路获得的曲折的思维过程作必要的设计,不只是讲教师加工整理好了的思维捷径 [5].笔者在带领学生解决这道题的教学时,就是围绕着渗透“求繁”的数学观念而展开,下面是笔者课堂教学的实录:
师:要证明不等式1+ 1 2 + 1 3 +…+ 1 n >ln 1+n + n 2 n+1?? n≥1 ①成立,大家有什么想法?
生1:如果获得不等式左边的前n项和的一个表达式,对问题的解决会带来很多好处,可是,我经过试探,很难找到这样的一个表达式(作为教师的笔者心理非常清楚,不等式①的左边是一个发散数列).
师:生1的这种想法,虽然在技术上我们难以得到执行,但是,我们可以分析生1想法的来源.他可能是这样想的:对于“不等号”(“等号”)也是一样,它们所连接的两边具有一种对等关系,他发现不等式①的这种形式不是对等的,加之以在“求简”的数学观念指令下,想到了求不等式①左边的一个表达式.可惜,我们办不到.怎么办?
生2:我们可以倒着想,既然①的左边的代数式不能直接相加得到一个结果,从而得到一个与①的右端形成一个“对等”的形式,那么,我想把①的右边转化为一个n项和的形式,如此也就形成了不等号的左右两边的“对等”形式了.但是,具体如何实现,我没有想好.
师:大家试探生2同学的这种观念是否可以实现?
说明,正如研究者分析中所产生的,在生2形成的观念的指令下,同学们找到了等式③、④,经由③、④又获得等式⑤,于是,要证明①成立,只要证明 1 2k + 1 2 k+1? >ln 1+ 1 k? ⑦成立就行了.
师:如何证明不等式⑦成立呢?
生3:第(Ⅱ)问提供的不等式肯定会起作用了.
说明:生3完整地给出了不等式①证明的思路.见解答的过程.
这种教学设计,数学教师对生1发生的数学观念的解释,揭示萌生“对等”的数学观念的过程是非常重要的,正是学生萌发出了这一数学观念的指令,形成了生2的处理这道题关键环节的技术性手段——萌生了“求繁”的数学观念.这个关键环节必须通过教师教学设计促使学生自己从自己的意识结构中生发出来,而不能“下载”给学生.这是实现数学解题教学的教育价值的最为重要的地方.
4 数学解题教学设计的一般程序
由这个例子我们可以归纳数学解题教学设计的一般程序:(1)教师针对某个数学问题尽可能多的获得解决的思路,教师最好的获得思路的方式是自己解题,因为,基于自己解题得到的思路,他会对自己的思路活动过程了如指掌,容易把握萌生某些数学观念的来源,从而容易发现解决问题的关键环节,教师抄别人解答的结果,就不可能对解题思路发现的过程具有如此深刻的体会;(2)确定解题过程的关键环节.解题过程的关键环节的主要标识就是指令问题思路中某些疑难步骤的数学观念是如何萌生的,这些基本上都是学生难以发生合适的数学观念的地方,它形成了培养学生创新能力的最佳资源;(3)依据学生发生数学知识的心理环节及其过渡性中介,经由选择教学法的加工,设计具体的解题教学流程.
5 简要结语
一位数学教师如果没有数学解题能力,他一定不可能成为非常优秀的数学教师;一位数学教学即使具有非常好的解题能力,他也未必一定能成为非常优秀的数学教师.数学解题能力构成了优秀数学教师的一项非常重要的必要条件,另一个非常重要的必要条件就是数学教师必须具备将解题能力转化为他的教学能力,对此,他需要特别关注学生发生数学问题思路的某些关键环节时学生的心理环节及其过渡性中介生成,从而设计教学过程循循善诱,引导学生依靠自己的认知结构的力量,重新萌生这种思路的关键环节,而不是将教师自己所得到的结果和盘托出地“下载”给学生,这其中,帮助学生萌生数学观念是数学教师在设计解题教学时需要特别注意的问题.对此,我们数学教师要思之再思,慎之 又慎.
参考文献
[1] 张昆,曹一鸣.完善数学教师教学行为的实现途径[J].数学教育学报,2015,23(1):33-37.
[2] 张昆,张乃达. 集中条件:数学解题的关键——教学设计的视角[J]. 中学数学(高中版),2016(2):9-12.
[3] ?张昆,罗增儒. 数學解题教学设计研究——指向渗透数学观念的视点[J]. 中学数学杂志,2017(11):15-18.
[4] 张乃达,过伯祥.张乃达数学教育——从思维到文化[M].济南:山东教育出版社,2007:186.
[5] 张昆.怎样备好数学课[J].中学教研(数学),1998(12):4.

