隧道运营期结构健康评价及MATLAB应用研究
金煜皓 王桂萱 赵杰
摘要:针对模糊层次综合评判方法计算的复杂性,使用MATLAB计算权重与模糊关系矩阵,并将两者综合得到模糊综合评判矩阵。最后以实际运营隧道为例,分析了模糊层次评价法的MATLAB程序在安全性评价中的应用。结果表明,将模糊层次综合评判法与MATLAB结合,能较好地进行隧道运营期结构健康评价。
关键词:模糊层次分析法;MATLAB应用;隧道健康评价
中图分类号:TU312 文献标识码:A 文章编号:1000-0666(2016)01-0120-06
0 引言
随着我国高速公路产业的快速发展,公路隧道的数量也呈直线增长态势。据统计,我国已有公路隧道11345座,总长9606km,年均增长率高达20%,且有逐年增速加快的趋势,已成为公路隧道工程建设规模和建设速度第一大国。然而,大部分已建隧道却存在着混凝土强度低、衬砌开裂、衬砌背后空洞、衬砌厚度不足等病害,这些病害不仅会给隧道本身带来严重的影响,而且有可能危及行车(人)的生命财产安全(王亚琼等,2014)。因此,对运营隧道结构健康状态的综合评价就显得十分重要。传统的隧道结构健康评价研究,大多仍停留在隧道施工期,且采用传统的定性方法,这是因为隧道结构性能受到多种因素的影响,具有很大的模糊性,无法用具体的数学公式准确定量表达。近年来部分学者运用建立数学模型的方法来描述运营隧道结构的安全性,洪平和刘鹏举(2011)用层次分析法模型分析了铁路运营隧道健康情况,但却无法消除层次分析法中特征值和特征向量复杂难求的缺陷,不利于工程应用。李云等(2010)利用多级模糊评价算法对已建隧道衬砌健康进行评价,但模糊评价模型没有程序化,在面临大量监测数据时,往往需要进行非常复杂的模糊计算,且结果精确度较差。
综上所述,已有的隧道运营期结构健康评价模型分析方法较为单一,仅有层次分析法或模糊评价法。另外,此类模型均没有实现全面的程序化,即没有建立一个全过程的结构评判程序化模型,这就导致了计算过程效率十分低下,计算结果不稳定且不准确。因此,为了能更好的对隧道结构健康状态做出科学的、合理的评价,有必要选用合适的评价方法,并对该方法的全过程进行程序化,以方便工程应用。
本文利用层次分析法求权重矩阵,模糊综合评价法求模糊关系矩阵,并通过建立隧道运营期结构健康指标体系及结构安全等级划分,将层次分析和模糊综合评判法相结合,建立隧道运营期结构模糊层次健康评价模型,并将此评价模型MATLAB程序化(宋飞,赵法锁,2008),最后以某实际公路隧道工程为例,说明模型的适用性与可靠性。
1 模糊层次分析法及公路隧道运营结构安全评价体系
1.1 层次分析法
层次分析法(The Analytic Hierarchy Process,简称AHP)在20世纪70年代中期由美国运筹学家Saaty正式提出。其分析步骤可分为建立层次结构体系、构造对比判断矩阵、计算权向量,并做一致性检验(Harker,Vargas,1987)。
层次分析法具有严格的上下层隶属关系,可运用1~9标度法,进行相对于上一层指标重要性的两两比较,得判断矩阵为
A=(aij)m×n. (1)式中:ni是第i个指标相对第j个指标的重要程度;矩阵A为互反矩阵,满足aij>0,aij=1/aij,aii=1。对于层次结构,从最顶层到最底层有几个隶属关系,就要建立几个指标因素判断矩阵。在建立了判断矩阵之后,关键是求出判断矩阵的最大特征值及该特征值对应的特征向量,所得特征向量即为权重向量。如矩阵A的特征值可由下式求得:
det(A-λI)=0. (2)式中:I为单位向量,λ为特征值,特征向量可由特征值进一步求得。从数学的角度来说,随着影响因素的增加,阶数变高,判断矩阵也会变得复杂,传统特征向量求解不仅越来越困难,而且求出的近似解的精度很差。研究表明,MATLAB可用来精确快速求解复杂矩阵的特征值和特征向量。
1.2 模糊综合评判法
模糊综合评判法是模糊数学中最常见的方法之一(James et al,2001),运用模糊及隶属度理论,考虑了不同指标对某一共同对象的综合影响,据此,对该共同对象进行等级划分。当某一事物被多种因素影响,但又无法精确给出每个影响因素对该事物的实际影响,就需要用到模糊综合评判法,而大多数事物往往受到不确定的各种因素的共同影响,因此模糊综合评判应用十分广泛。模糊综合评价具体过程如下:将影响事物的多种因素看成一组模糊集合,称之为因素集u,每个因素u都需要一组评判值进行评判,故设立评判集v,而每个u对每个v都有相对应且唯一的隶属关系,此隶属关系是模糊的,不是精确的,所有u对所有v的隶属关系所组成的集合称之为隶属度矩阵(模糊关系矩阵R),将得到的模糊关系矩阵R与因素u所对应的权重进行模糊合成,就得到评价的定量解值,根据隶属度最大原则,按照划分好的等级,求出事物的等级。上述即为模糊综合评价过程,其优点是将不确定的、模糊的关系定量化,最大程度减少人为和定性所造成的误差。其缺点是在对权重指标的确定过程中,主观性较强,针对模糊综合评价求权重的缺点,可采用层次分析法求权重,并与模糊综合评价法相结合,通过模糊矩阵合成,求出事物等级。
1.3 隧道运营安全评价体系
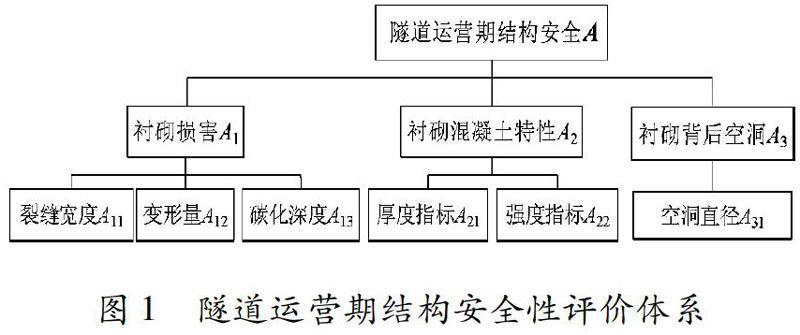
参考目前国内外已有的研究成果(戴忧华等,2010)和《公路隧道养护技术规范》(JTG H12-2003)以及指标选取原则,同时考虑本文的研究范围,选取仅考虑无特殊地质条件,且无深埋的公路隧道洞身标准断面衬砌结构为研究对象。结合层次分析法和模糊综合评价理论,建立公路隧道运营期结构安全性评价体系,如图1所示。由图1可知,隧道主体结构模糊层次评价模型分为3层:第一层为目标层,即隧道运营期结构安全状态A;第二层为准则层,因隧道运营期结构安全主要受衬砌影响,根据重点突出,少而精且互不影响原则,可分为衬砌损害A1,衬砌混凝土特性A2,衬砌背后空洞A3,这3个因素组成了隧道结构安全评价体系的制约因素集;第三层为指标层,反映了影响上一层即准则层的最可能的影响因素,各指标为:裂缝宽度A11变形量A12碳化深度A13,混凝土厚度指标A21、混凝土强度指标A22,衬砌空洞直径A31。
2 公路隧道运营安全等级划分
常见的几种安全等级划分法中,三级划分法过于简单,五级划分法实质是在四级划分法基础上对某项进行了细化,十级划分法又划分过细,很多状态是不需要的,因此笔者参考已有运营隧道结构安全等级划分情况,综合分析各种划分法的优缺点,选用四级划分法作为隧道运营期结构安全性等级划分的依据:Ⅰ级为隧道结构非常安全,衬砌无损伤;Ⅱ级为隧道基本安全,衬砌轻微受损;Ⅲ级为隧道结构不安全,衬砌存在裂缝,背后出现空洞;Ⅳ级为隧道结构严重破坏,衬砌大面积掉块,危及行车安全。
3 模糊层次综合评价模型的MATLAB程序实现
3.1 特征向量及一致性检验的MATLAB实现
MATLAB可以精确快速地求解层次分析法中复杂矩阵特征值与特征向量,可调用eig函数进行求解。MATLAB中具体编程如下,定义M函数MAX-eigvalvec.m:
function[eigval,w]=MAX-eigvalvec(A);%求最大特征值和归一化的特征向量,A为判断矩阵;
[eigvec,eigval]=eig(A);
maxeigval=max(eigval);%最大特征值;
v=eigvec(:,index);%最大特征值对应的特征向量;
w=v./sum(v);%特征向量归一化;
end
层次分析法要求必须对各层次间的判断矩阵进行一致性检验。这是为了避免同一层中A比B重要,B比C重要,而C却比A重要的错误出现。定义s-examine.m函数实现一致性检验:
function[RI,CI]=s-examine(maxeigval,A);%单排序一致性检验;
n=size(A,1);
RIT=[0.0 0.0 0.58 0.90 1.12 1.24 1.32 1.411.45 1.49 1.51 1.54 1.56 1.58 1.59];
RI=RIT(n);%随机一致性指标;
CI=(maxeigval-n)/(n-1);%一致性指标;
CR=CI/RI;
if CR>=0.1
disp([input(‘矩阵没有通过一致性检验,请重新调整判断矩阵)]);
else
disp([input(‘矩阵通过一致性检验)]);
end
3.2 MATLAB模糊综合评判模型
定义模糊综合评价M函数Fuzzy_F.m,在MATLAB实现如下:
function R=Fuzzy_F(A1,A2,~Am);%A1~Am为指标层实际监测值;
R=zeros(m,n);%m行,n列空矩阵,作为所求模糊关系矩阵R的存放空间;
S=[S11S12…S12S1n;S21S22…S12S2n;Sm1Sm2…Smn];%评价标准,即各影响因素的隶属函数参数,可结合评判基准求得;
T=zeios(1,i);
T(1,1)=A1;T(1,2)=A2;T(1,3)=A3;~T(1,m)=Am;%将实际影响因素值赋予T中;
for i=1:m;
R(i,1)=fi1(T(i),S(i,)..);
R(i,2)=fi2(T(i),S(i,)..);
R(i,3)=fi3(T(i),S(i,)..);
R(i,4)=fi4(T(i),S(i,)..);
end
上述程序是将T(1,i)代入隶属度函数,计算隶属度矩阵(模糊关系矩阵),这4个隶属度函数,对应所划分的4个等级,该程序实现了所列影响因素实际值分别隶属Ⅰ、Ⅱ、Ⅲ和Ⅳ四个安全等级的隶属程度,即隶属度矩阵Ro而隶属函数构造的好坏直接决定评价系统的优劣,一般而言,隶属函数有模糊统计方法、三分法、模糊分步法、专家评分法等,考虑到统计方法需要较多样本,专家评分法主观性较强,故隶属函数常常采用模糊分布法。遵循隶属函数确定的原则和方法,结合苏永华(2007)关于模糊隶属函数的构造方法研究以及对各分布模型进行对比分析,本文选取模糊分布法中的“降半梯形”作为指标层各指标的隶属函数。
3.3 模糊层次评判结果MATLAB实现
经综合比较分析,本文采用加权平均模糊算子,进而将层次分析法所得权重矩阵与模糊综合评价所得隶属矩阵进行加权模糊结合,选用加权平均模糊算子,即先将两个矩阵里的数对应相乘后相加M(·,①),MATLAB程序实现如下,定义M函数jq(w,R):
function WR=jq(w,R);
m=size(W,1);n=size(R,2);
for i-1:W
for j=1:R
WR(i,j)=sum(w(i,:).*R(:,j));
end
end
B=WR./sum(WR);%对矩阵归一化,B为模糊合成矩阵,由最大隶属原则,确定模型等级。
4 实例分析
某运营10年隧道为双向二车道隧道,左线起讫桩号为K195+620~K197+390,全长1700m;右线起讫桩号为YK195+619~YK197+369,全长1740m。本隧道通过地段地层结构简单,地表均为第四系全新统(Q4)残坡积层所覆盖,隧道穿越处最高标高为360m。该隧道由于运营时间较长,其衬砌结构已出现不同程度的损坏现象,因此有必要对其结构健康进行安全性评价。
另外,由于国内外对隧道运营期结构健康评估还处于起步阶段,更缺少完整的程序化的评价模型,因而文中对该隧道运营期结构安全进行基于程序化模型的分析,说明模糊层次分析在隧道运营期结构健康评价中的MATLAB应用。
4.1 权重设计及模糊隶属度矩阵计算
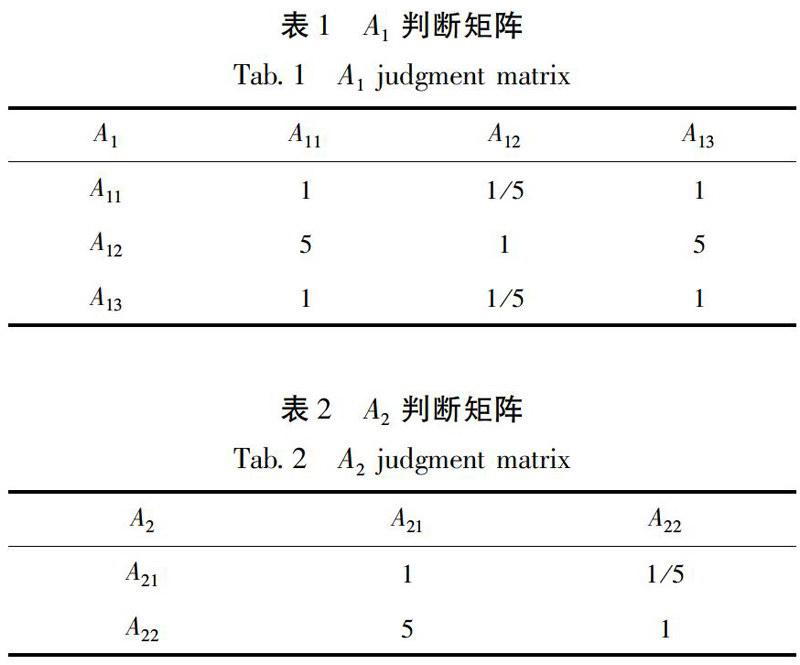
针对层次分析法求权重中的标度选用问题,骆正清和杨善林(2004)对常用的几种层次分析法标度进行比较,得出对单一准则下的排序,1~9标度较好;对多准则下的排序,指数标度更好。综上分析,依据图1的安全层次结构,参考工程经验,利用1~9标度法,对监测到的该隧道各个具体影响因素实际数值进行两两比较评分,得判断矩阵,如表1~3所示。
对背后空洞直径指标,因为其只有一项,故A31=[1]。
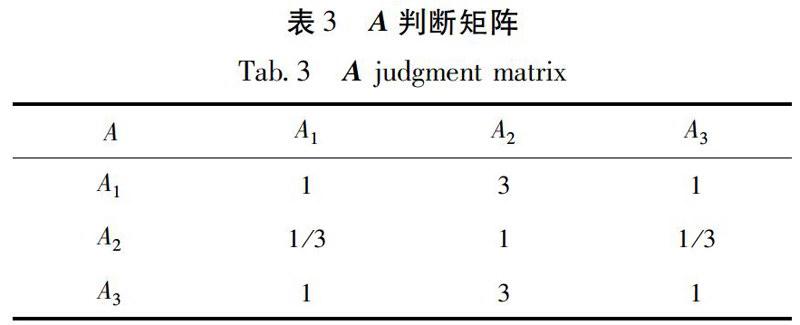
对准则层指标进行两两比较评分,得判断矩阵,如表3所示。
根据上述判断矩阵,在MATLAB的CommandWindow中键入如下命令,可迅速得出各层的权重矩阵:
A=[131;1/311/3;131];
[maxA,wA]=maxeigvalvec(A);
可得
[ωA]=[0.4286 0.1429 0.4286];
同理可得
[ωA1]=[0.1429 0.7143 0.1429];
[ωA2]=[0.1667 0.8333];
[ωA3]=[1].
基于MATLAB程序求模糊隶属度矩阵,其中,隧道运营期结构安全隶属函数参数为S=[0.050.217 0.05 0.217 0.417 0.217 0.417 0.75 0.417O.75:0.05 0.217 0.05 0.217 0.417 0.217 0.4170.75 0.417 0.75;0.5 2 0.5 2 4 2 4 6 4 6;050 0 50 300 50 300 600 300 600:0.5 2 0.5 26.5 2 6.5 12 6.5 12:0.5 2 0.5 2 3.5 2 3.54.5 3.5 4.5],进而根据现场传感器采集到的监测数据,并调用本文所用隶属度函数及Fuzzy_F.m函数,在Command Window中键入以下代码:
R=Fuzzy_FA1(0.5,0.5,0.5);
得A1所包含的指标层影响因素对应的隶属度矩阵:
将现场监测数据A21=0.05,A22=0.05,A31=0代入相应Fuzzy_F.m函数,得:
4.2 一级模糊综合评判
将由MATLAB编程得到的权重向量W与模糊关系矩阵R进行加权平均模糊合成,在CommandWindow中键入如下命令:
C(A1)=jq(WA1,RA1);该语句实现了WA1与RA1加权模糊合成;
B(A1)=C(A1)./sum(C(A1));表示对模糊合成的矩阵进行归一化;
点击回车键,得:
B(A1)=[0.142 9 0 0.643 5 0.213 6].
同理可得:
B(A2)=[1 0 0 0];
B(A3)=[1 0 0 0].
综上可得一级模糊层次综合评判矩阵为
4.3 二级模糊综合评判
A表示其所包含的准则层的3个影响因素,将WA与RA进行加权模糊合成:
C(A)=jq(WA,RA);
对模糊合成的矩阵进行归一化:
B(A)=C(A)./sum(C(A));得
B(A)=[0.6327 0 0.2758 0.0915].
由以上二级模糊综合评判计算结果,并根据最大隶属原则,0.6327最大,所以运营隧道结构处于Ⅰ级状态,即结构很安全,这与该运营隧道实际情况一致,但相对而言,0.2758(Ⅲ级)也较大,说明隧道安全还是存在风险,再加上隧道衬砌结构随着时间的增长,影响其安全的各个指标也会有所下降,必然会对运营隧道结构安全带来威胁,所以应当采取合适的安全措施。
5 结论
针对运营隧道结构健康评价问题,建立基于模糊层次综合评价法的程序模型,通过分析得出如下结论:
(1)将层次分析法和模糊评价法相结合,建立隧道运营期结构安全模糊层次评价模型,克服了评价过程中主观随意性的缺点,选用“降半梯形”作为指标层各指标的隶属函数,使得评价结果更符合客观实际。
(2)利用MATLAB语言实现了评价模型建立全过程的程序化,程序化后模型不仅可以极大缩短传统模型计算时间,也显著提高了计算结果的精度和准确度,为隧道运营期结构健康评价系统开发提供所需的应用程序。
(3)以实际隧道运营期结构健康评价为例,结果表明,将模糊层次综合评判法结合MATLAB应用,能较好地进行隧道运营期结构健康评价,是一种开展运营隧道结构安全风险分析的有效方法。



摘要:针对模糊层次综合评判方法计算的复杂性,使用MATLAB计算权重与模糊关系矩阵,并将两者综合得到模糊综合评判矩阵。最后以实际运营隧道为例,分析了模糊层次评价法的MATLAB程序在安全性评价中的应用。结果表明,将模糊层次综合评判法与MATLAB结合,能较好地进行隧道运营期结构健康评价。
关键词:模糊层次分析法;MATLAB应用;隧道健康评价
中图分类号:TU312 文献标识码:A 文章编号:1000-0666(2016)01-0120-06
0 引言
随着我国高速公路产业的快速发展,公路隧道的数量也呈直线增长态势。据统计,我国已有公路隧道11345座,总长9606km,年均增长率高达20%,且有逐年增速加快的趋势,已成为公路隧道工程建设规模和建设速度第一大国。然而,大部分已建隧道却存在着混凝土强度低、衬砌开裂、衬砌背后空洞、衬砌厚度不足等病害,这些病害不仅会给隧道本身带来严重的影响,而且有可能危及行车(人)的生命财产安全(王亚琼等,2014)。因此,对运营隧道结构健康状态的综合评价就显得十分重要。传统的隧道结构健康评价研究,大多仍停留在隧道施工期,且采用传统的定性方法,这是因为隧道结构性能受到多种因素的影响,具有很大的模糊性,无法用具体的数学公式准确定量表达。近年来部分学者运用建立数学模型的方法来描述运营隧道结构的安全性,洪平和刘鹏举(2011)用层次分析法模型分析了铁路运营隧道健康情况,但却无法消除层次分析法中特征值和特征向量复杂难求的缺陷,不利于工程应用。李云等(2010)利用多级模糊评价算法对已建隧道衬砌健康进行评价,但模糊评价模型没有程序化,在面临大量监测数据时,往往需要进行非常复杂的模糊计算,且结果精确度较差。
综上所述,已有的隧道运营期结构健康评价模型分析方法较为单一,仅有层次分析法或模糊评价法。另外,此类模型均没有实现全面的程序化,即没有建立一个全过程的结构评判程序化模型,这就导致了计算过程效率十分低下,计算结果不稳定且不准确。因此,为了能更好的对隧道结构健康状态做出科学的、合理的评价,有必要选用合适的评价方法,并对该方法的全过程进行程序化,以方便工程应用。
本文利用层次分析法求权重矩阵,模糊综合评价法求模糊关系矩阵,并通过建立隧道运营期结构健康指标体系及结构安全等级划分,将层次分析和模糊综合评判法相结合,建立隧道运营期结构模糊层次健康评价模型,并将此评价模型MATLAB程序化(宋飞,赵法锁,2008),最后以某实际公路隧道工程为例,说明模型的适用性与可靠性。
1 模糊层次分析法及公路隧道运营结构安全评价体系
1.1 层次分析法
层次分析法(The Analytic Hierarchy Process,简称AHP)在20世纪70年代中期由美国运筹学家Saaty正式提出。其分析步骤可分为建立层次结构体系、构造对比判断矩阵、计算权向量,并做一致性检验(Harker,Vargas,1987)。
层次分析法具有严格的上下层隶属关系,可运用1~9标度法,进行相对于上一层指标重要性的两两比较,得判断矩阵为
A=(aij)m×n. (1)式中:ni是第i个指标相对第j个指标的重要程度;矩阵A为互反矩阵,满足aij>0,aij=1/aij,aii=1。对于层次结构,从最顶层到最底层有几个隶属关系,就要建立几个指标因素判断矩阵。在建立了判断矩阵之后,关键是求出判断矩阵的最大特征值及该特征值对应的特征向量,所得特征向量即为权重向量。如矩阵A的特征值可由下式求得:
det(A-λI)=0. (2)式中:I为单位向量,λ为特征值,特征向量可由特征值进一步求得。从数学的角度来说,随着影响因素的增加,阶数变高,判断矩阵也会变得复杂,传统特征向量求解不仅越来越困难,而且求出的近似解的精度很差。研究表明,MATLAB可用来精确快速求解复杂矩阵的特征值和特征向量。
1.2 模糊综合评判法
模糊综合评判法是模糊数学中最常见的方法之一(James et al,2001),运用模糊及隶属度理论,考虑了不同指标对某一共同对象的综合影响,据此,对该共同对象进行等级划分。当某一事物被多种因素影响,但又无法精确给出每个影响因素对该事物的实际影响,就需要用到模糊综合评判法,而大多数事物往往受到不确定的各种因素的共同影响,因此模糊综合评判应用十分广泛。模糊综合评价具体过程如下:将影响事物的多种因素看成一组模糊集合,称之为因素集u,每个因素u都需要一组评判值进行评判,故设立评判集v,而每个u对每个v都有相对应且唯一的隶属关系,此隶属关系是模糊的,不是精确的,所有u对所有v的隶属关系所组成的集合称之为隶属度矩阵(模糊关系矩阵R),将得到的模糊关系矩阵R与因素u所对应的权重进行模糊合成,就得到评价的定量解值,根据隶属度最大原则,按照划分好的等级,求出事物的等级。上述即为模糊综合评价过程,其优点是将不确定的、模糊的关系定量化,最大程度减少人为和定性所造成的误差。其缺点是在对权重指标的确定过程中,主观性较强,针对模糊综合评价求权重的缺点,可采用层次分析法求权重,并与模糊综合评价法相结合,通过模糊矩阵合成,求出事物等级。
1.3 隧道运营安全评价体系
参考目前国内外已有的研究成果(戴忧华等,2010)和《公路隧道养护技术规范》(JTG H12-2003)以及指标选取原则,同时考虑本文的研究范围,选取仅考虑无特殊地质条件,且无深埋的公路隧道洞身标准断面衬砌结构为研究对象。结合层次分析法和模糊综合评价理论,建立公路隧道运营期结构安全性评价体系,如图1所示。由图1可知,隧道主体结构模糊层次评价模型分为3层:第一层为目标层,即隧道运营期结构安全状态A;第二层为准则层,因隧道运营期结构安全主要受衬砌影响,根据重点突出,少而精且互不影响原则,可分为衬砌损害A1,衬砌混凝土特性A2,衬砌背后空洞A3,这3个因素组成了隧道结构安全评价体系的制约因素集;第三层为指标层,反映了影响上一层即准则层的最可能的影响因素,各指标为:裂缝宽度A11变形量A12碳化深度A13,混凝土厚度指标A21、混凝土强度指标A22,衬砌空洞直径A31。
2 公路隧道运营安全等级划分
常见的几种安全等级划分法中,三级划分法过于简单,五级划分法实质是在四级划分法基础上对某项进行了细化,十级划分法又划分过细,很多状态是不需要的,因此笔者参考已有运营隧道结构安全等级划分情况,综合分析各种划分法的优缺点,选用四级划分法作为隧道运营期结构安全性等级划分的依据:Ⅰ级为隧道结构非常安全,衬砌无损伤;Ⅱ级为隧道基本安全,衬砌轻微受损;Ⅲ级为隧道结构不安全,衬砌存在裂缝,背后出现空洞;Ⅳ级为隧道结构严重破坏,衬砌大面积掉块,危及行车安全。
3 模糊层次综合评价模型的MATLAB程序实现
3.1 特征向量及一致性检验的MATLAB实现
MATLAB可以精确快速地求解层次分析法中复杂矩阵特征值与特征向量,可调用eig函数进行求解。MATLAB中具体编程如下,定义M函数MAX-eigvalvec.m:
function[eigval,w]=MAX-eigvalvec(A);%求最大特征值和归一化的特征向量,A为判断矩阵;
[eigvec,eigval]=eig(A);
maxeigval=max(eigval);%最大特征值;
v=eigvec(:,index);%最大特征值对应的特征向量;
w=v./sum(v);%特征向量归一化;
end
层次分析法要求必须对各层次间的判断矩阵进行一致性检验。这是为了避免同一层中A比B重要,B比C重要,而C却比A重要的错误出现。定义s-examine.m函数实现一致性检验:
function[RI,CI]=s-examine(maxeigval,A);%单排序一致性检验;
n=size(A,1);
RIT=[0.0 0.0 0.58 0.90 1.12 1.24 1.32 1.411.45 1.49 1.51 1.54 1.56 1.58 1.59];
RI=RIT(n);%随机一致性指标;
CI=(maxeigval-n)/(n-1);%一致性指标;
CR=CI/RI;
if CR>=0.1
disp([input(‘矩阵没有通过一致性检验,请重新调整判断矩阵)]);
else
disp([input(‘矩阵通过一致性检验)]);
end
3.2 MATLAB模糊综合评判模型
定义模糊综合评价M函数Fuzzy_F.m,在MATLAB实现如下:
function R=Fuzzy_F(A1,A2,~Am);%A1~Am为指标层实际监测值;
R=zeros(m,n);%m行,n列空矩阵,作为所求模糊关系矩阵R的存放空间;
S=[S11S12…S12S1n;S21S22…S12S2n;Sm1Sm2…Smn];%评价标准,即各影响因素的隶属函数参数,可结合评判基准求得;
T=zeios(1,i);
T(1,1)=A1;T(1,2)=A2;T(1,3)=A3;~T(1,m)=Am;%将实际影响因素值赋予T中;
for i=1:m;
R(i,1)=fi1(T(i),S(i,)..);
R(i,2)=fi2(T(i),S(i,)..);
R(i,3)=fi3(T(i),S(i,)..);
R(i,4)=fi4(T(i),S(i,)..);
end
上述程序是将T(1,i)代入隶属度函数,计算隶属度矩阵(模糊关系矩阵),这4个隶属度函数,对应所划分的4个等级,该程序实现了所列影响因素实际值分别隶属Ⅰ、Ⅱ、Ⅲ和Ⅳ四个安全等级的隶属程度,即隶属度矩阵Ro而隶属函数构造的好坏直接决定评价系统的优劣,一般而言,隶属函数有模糊统计方法、三分法、模糊分步法、专家评分法等,考虑到统计方法需要较多样本,专家评分法主观性较强,故隶属函数常常采用模糊分布法。遵循隶属函数确定的原则和方法,结合苏永华(2007)关于模糊隶属函数的构造方法研究以及对各分布模型进行对比分析,本文选取模糊分布法中的“降半梯形”作为指标层各指标的隶属函数。
3.3 模糊层次评判结果MATLAB实现
经综合比较分析,本文采用加权平均模糊算子,进而将层次分析法所得权重矩阵与模糊综合评价所得隶属矩阵进行加权模糊结合,选用加权平均模糊算子,即先将两个矩阵里的数对应相乘后相加M(·,①),MATLAB程序实现如下,定义M函数jq(w,R):
function WR=jq(w,R);
m=size(W,1);n=size(R,2);
for i-1:W
for j=1:R
WR(i,j)=sum(w(i,:).*R(:,j));
end
end
B=WR./sum(WR);%对矩阵归一化,B为模糊合成矩阵,由最大隶属原则,确定模型等级。
4 实例分析
某运营10年隧道为双向二车道隧道,左线起讫桩号为K195+620~K197+390,全长1700m;右线起讫桩号为YK195+619~YK197+369,全长1740m。本隧道通过地段地层结构简单,地表均为第四系全新统(Q4)残坡积层所覆盖,隧道穿越处最高标高为360m。该隧道由于运营时间较长,其衬砌结构已出现不同程度的损坏现象,因此有必要对其结构健康进行安全性评价。
另外,由于国内外对隧道运营期结构健康评估还处于起步阶段,更缺少完整的程序化的评价模型,因而文中对该隧道运营期结构安全进行基于程序化模型的分析,说明模糊层次分析在隧道运营期结构健康评价中的MATLAB应用。
4.1 权重设计及模糊隶属度矩阵计算
针对层次分析法求权重中的标度选用问题,骆正清和杨善林(2004)对常用的几种层次分析法标度进行比较,得出对单一准则下的排序,1~9标度较好;对多准则下的排序,指数标度更好。综上分析,依据图1的安全层次结构,参考工程经验,利用1~9标度法,对监测到的该隧道各个具体影响因素实际数值进行两两比较评分,得判断矩阵,如表1~3所示。
对背后空洞直径指标,因为其只有一项,故A31=[1]。
对准则层指标进行两两比较评分,得判断矩阵,如表3所示。
根据上述判断矩阵,在MATLAB的CommandWindow中键入如下命令,可迅速得出各层的权重矩阵:
A=[131;1/311/3;131];
[maxA,wA]=maxeigvalvec(A);
可得
[ωA]=[0.4286 0.1429 0.4286];
同理可得
[ωA1]=[0.1429 0.7143 0.1429];
[ωA2]=[0.1667 0.8333];
[ωA3]=[1].
基于MATLAB程序求模糊隶属度矩阵,其中,隧道运营期结构安全隶属函数参数为S=[0.050.217 0.05 0.217 0.417 0.217 0.417 0.75 0.417O.75:0.05 0.217 0.05 0.217 0.417 0.217 0.4170.75 0.417 0.75;0.5 2 0.5 2 4 2 4 6 4 6;050 0 50 300 50 300 600 300 600:0.5 2 0.5 26.5 2 6.5 12 6.5 12:0.5 2 0.5 2 3.5 2 3.54.5 3.5 4.5],进而根据现场传感器采集到的监测数据,并调用本文所用隶属度函数及Fuzzy_F.m函数,在Command Window中键入以下代码:
R=Fuzzy_FA1(0.5,0.5,0.5);
得A1所包含的指标层影响因素对应的隶属度矩阵:
将现场监测数据A21=0.05,A22=0.05,A31=0代入相应Fuzzy_F.m函数,得:
4.2 一级模糊综合评判
将由MATLAB编程得到的权重向量W与模糊关系矩阵R进行加权平均模糊合成,在CommandWindow中键入如下命令:
C(A1)=jq(WA1,RA1);该语句实现了WA1与RA1加权模糊合成;
B(A1)=C(A1)./sum(C(A1));表示对模糊合成的矩阵进行归一化;
点击回车键,得:
B(A1)=[0.142 9 0 0.643 5 0.213 6].
同理可得:
B(A2)=[1 0 0 0];
B(A3)=[1 0 0 0].
综上可得一级模糊层次综合评判矩阵为
4.3 二级模糊综合评判
A表示其所包含的准则层的3个影响因素,将WA与RA进行加权模糊合成:
C(A)=jq(WA,RA);
对模糊合成的矩阵进行归一化:
B(A)=C(A)./sum(C(A));得
B(A)=[0.6327 0 0.2758 0.0915].
由以上二级模糊综合评判计算结果,并根据最大隶属原则,0.6327最大,所以运营隧道结构处于Ⅰ级状态,即结构很安全,这与该运营隧道实际情况一致,但相对而言,0.2758(Ⅲ级)也较大,说明隧道安全还是存在风险,再加上隧道衬砌结构随着时间的增长,影响其安全的各个指标也会有所下降,必然会对运营隧道结构安全带来威胁,所以应当采取合适的安全措施。
5 结论
针对运营隧道结构健康评价问题,建立基于模糊层次综合评价法的程序模型,通过分析得出如下结论:
(1)将层次分析法和模糊评价法相结合,建立隧道运营期结构安全模糊层次评价模型,克服了评价过程中主观随意性的缺点,选用“降半梯形”作为指标层各指标的隶属函数,使得评价结果更符合客观实际。
(2)利用MATLAB语言实现了评价模型建立全过程的程序化,程序化后模型不仅可以极大缩短传统模型计算时间,也显著提高了计算结果的精度和准确度,为隧道运营期结构健康评价系统开发提供所需的应用程序。
(3)以实际隧道运营期结构健康评价为例,结果表明,将模糊层次综合评判法结合MATLAB应用,能较好地进行隧道运营期结构健康评价,是一种开展运营隧道结构安全风险分析的有效方法。

