基于ANSYS/LS—DYNA的矿区地下巷道三维动力响应分析
刘书贤 刘少栋 魏晓刚 麻凤海

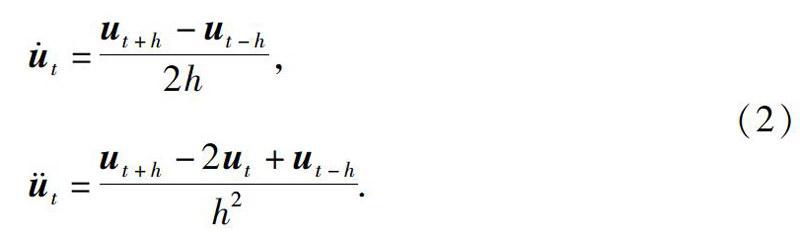
摘要:为研究煤矿地下巷道在地震作用下的动力响应,考虑巷道结构的损伤效应,基于显式算法的土结构体系动力学方程,建立ANSYS/LS-DYNA三维数值模型,并在模型指定位置设置观测点。通过观测点的动力响应特征研究巷道的动态响应。结果表明:巷道在地震作用下,半拱形巷道应力主要分布在拱帮和墙角立板、底板处,且拱帮和墙角处塑性体积应变明显,巷道墙角处的损伤明显大于其他各部,是巷道容易发生破坏的部位。
关键词:地下巷道;动力响应;有限元分析;地震作用;ANSYS/LS-DYNA
中图分类号:TD32 文献标识码:A 文章编号:1000-0666(2016)01-0022-06
0 引言
近年来,随着我国煤炭资源开采的增多,我国煤矿区形成了大量形式各异、大小功能不同、纵横交错的地下巷道。我国80%的矿区处于地震多发区,由于缺少完善的地下结构抗震设计规范,巷道在地震作用下的稳定性值得我们关注,因此研究巷道的地震动力响应特征及其变化规律十分必要。孙超等(2009)已经对地下结构的动力稳定性问题做了大量研究:刘晶波等(2005)对地铁盾构隧道的地震响应进行了数值分析;刘书贤等(2013)研究了煤矿采动与地震耦合作用下建筑物灾变机理;章泳健等(2010)基于LS-DY-NA研究了隧道的初应力计算方法;姜耀东等(2005)分析了放炮震动引发煤矿巷道动力失稳的机理;高富强等(2009)分析了动力扰动下巷道围岩力学响应。
对于地下结构的研究比较多的是对地铁等浅埋结构的研究,但对于地震作用下巷道响应的研究较少,且考虑因素单一,对于巷道结构在地震中的损伤(赵宝友,2009)、岩层分布及其与巷道的接触和波动效应未给予充分的考虑。本文针对煤矿开采地下巷道在初始应力场和地震共同作用下巷道的地震响应研究的不足,基于ANSYS/LS-DYNA的显式动力有限元模型,考虑巷道在地震过程中的损伤及巷道与围岩的接触效应,在模型边界设置无反射边界,对煤矿采煤地下巷道进行了三维数值地震动响应分析研究。
1 巷道围岩-结构体系动力有限元分析
由于巷道结构与围岩之间存在相互作用,在分析巷道围岩体系结构的同时还要对结构围岩进行分析。围岩作为一种半无限介质,在数值计算中一方面主要是通过引入人工边界(如粘性边界、粘弹性边界等)模拟连续介质的辐射阻尼,保证散射波能量从有限区域穿过人工边界(何伟,2011)。另一方面是模拟围岩的非线性,本文考虑围岩材料非线性和接触非线性,围岩采用D-P理想弹塑性模型,就可以很好地描述围岩的非线性行为。
1.1 巷道围岩-结构体系动力方程
根据达朗贝尔原理可以建立该体系地震动作用下任意时刻有限元平衡方程(克拉夫,彭津,2006):
Mü+Cu+Ku=P. (1)式中,M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,P是节点荷载向量;u、u、ü分别是体系的位移、速度和加速度。该运动方程一般将整个地震过程分成若干微小时间段h,假设体系在微小时间段内体系是线性变化的,然后采用直接积分法解得,LS-DYNA采用显式中心差分法,即:
阻尼采用Rayleigh阻尼,它是将结构整体阻尼矩阵C表示成整体质量矩阵M和整体刚度矩阵K的线性组合:C=αM+βK,式中比例常数α和β阻尼系数可以由振型阻尼比计算得到,在LS-DYNA中通过关键字:*DAMPING设置(ISCT,2007)。
2 地震作用下巷道-围岩动力失稳演化分析
2.1 有限元分析模型
建立三维有限元模型,模型尺寸为y向610m,X向660m,Z向300m;岩层和巷道物理力学性能如表1,岩层分布如表2。巷道为半拱形巷道,拱直径4m,巷道的纵向长度为200m,衬砌厚度为400mm。围岩和巷道衬砌使用solid164体单元,人工边界采用无反射边界。岩层材料采用理想弹塑性DP材料,巷道结构采用C50混凝土,LS-DYNA中通过*MAT_072113材料模型实现巷道损伤本构。
2.2 地震波的选取与调整
国内外研究表明,选取地震波需满足强度、频谱特性、波的持时的要求,不同地震波参数得出的地震响应可能相差明显,因而选择合理的地震波参数进行动力分析是必要的。本文选用了15s的El Centro地震波,最大加速度调整为150cm/s2,如图2所示,地震波在基岩底部沿X水平输入。
2.3 数值模拟结果分析
在巷道100m处截取截面,并在截面不同部位设置观测点,如图3所示。
2.3.1 巷道应力分析
图4为巷道应力的典型分布图,从图中可知,巷道的等效应力和S1主要分布在墙角和拱帮偏下,S3主要分布两侧拱腰处;最大剪应力在墙角处最大,拱帮偏下处次之;这说明巷道的墙角立板和拱腰处成了高应力集中区。
图5为巷道取100m纵深截面时不同部位的最大应力(等效、S1、S3、剪应力),由图可知,等效应力、S3和最大剪应力的峰值在左右拱帮偏下的位置(5、6、7、26、27、28号点)和墙角立板的位置(12、13、20、21号点);S1峰值在左右拱帮偏下(8号点)和左右立板腰部(10、11、22、23号点)位置;这说明巷道的拱帮偏下和墙角是拉、剪复合最大应力区,巷道的立板腰部主要受拉应力作用;地震作用下的高应力反复的加、卸载会对巷道的这些部位造成较大破坏,对于在拉、剪复合应力区的拱帮和墙角破坏更明显,墙角处尤其明显。
2.3.2 损伤分析
图6为巷道的塑性体积应变,从图中可知巷道拱帮发生了明显的塑性体积应变,且由巷道中部向巷道两端扩展时,巷道的塑性体积应变有减小的趋势,但是在巷道的两个端部又有所增大,造成巷道两端塑性体积应变有所增大的主要原因是端部边界条件不同;其次在巷道内侧的墙角处也出现了明显的塑性体积应变,在巷道发生塑性体积应变的部位(巷道帮部、腰部至墙角立板)积累了明显的损伤,这些损伤使得巷道在这些部位更容易遭到破坏。
图7为巷道取100m纵深截面时不同部位的最大塑性体积应变,由图可知,巷道的左右帮部(5、28号点)和墙角底板(13、20号点)的塑性体积应变最为明显,这说明巷道的左右帮部和墙角底板会发生相对于其他部位更明显的变形,这可能造成帮部开裂、墙角底板翘起,同时伴随着小块石飞溅。由于巷道的墙角立板(13、21号点)和帮部偏上(5、28号点)的塑性变形较为明显,因此在这两处积累损伤较为明显,其中墙角底板损伤尤为严重,这说明在地震作用过程中,墙角立板在拉、剪应力反复作用下会积累大量的损伤,拱帮偏上损伤程度也要明显大于其他部位,这会造成墙角立板和拱帮偏上处最先发生破坏,随着这种破坏的扩展,就可能引发立板和上帮失效,进而引发整个巷道的破坏。
2.3.3 时程分析
由上述可知,地震作用过程中巷道的墙角处应力最为复杂,变形最为明显。本节提取了巷道墙角12和13号观测单元的应力和塑性体积应变的时程曲线。分析图8的巷道墙角立板和底板的应力时程曲线可知:巷道墙角的应力在t=2s和f=8s会出现两个峰值,在基道取100m纵深截面的前提下,t=2s时的应力峰值与输入加速度的峰值时刻基本一致,t=8s的应力峰值较加速度峰值有所提前;巷道墙角立板的等效应力在整个时程中小于墙角底板的等效应力,S1应力的墙角立板的应力大于底板的应力,S3应力中间时刻较为明显,最大剪应力墙角底板在整个过程中基本大于立板。
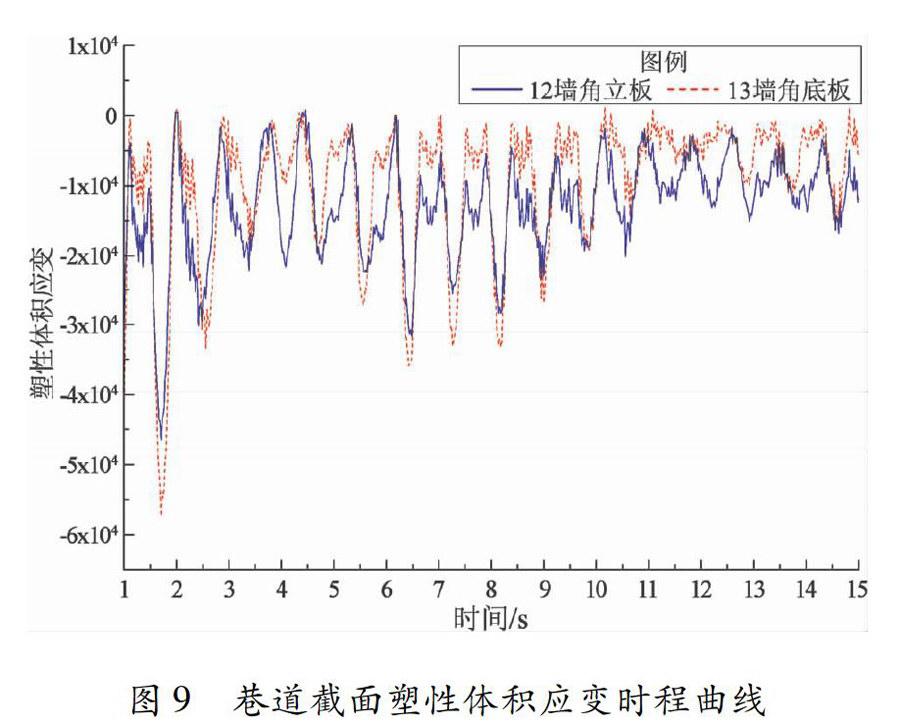
图9为巷道墙角的塑性体积应变时程曲线。由时程曲线可知立板和底板的塑性体积应变变化基本一致,底板的塑性体积应变大于立板的,从而使得底板的损伤大于立板。故可得出在整个地震过程中,半拱形巷道的墙角底板应作为抗震的重点防护部位。
3 结论与讨论
本文基于显式动力有限元理论,分析研究了地震作用下地下巷道结构动力响应及其损伤破坏,利用ANSYS/LS-DYNA建立了地下巷道地震作用下的三维计算模型,通过有限元分析计算得到如下结论:
(1)地震作用下巷道结构的拱帮和墙角处会出现周期性高应力集中区域,在墙角处会出现拉、剪同时达到最大,说明了半拱形巷道的拱帮和墙角最容易发生动力破坏,在巷道的拱帮偏下和墙角处会发生明显的塑性变形以及发生较严重的损伤,需要重视对巷道结构拱帮和墙角的设计,同时也要及时进行加固维护,以保证巷道结构的安全使用。
(2)地震动力荷载作用下巷道的拱帮和墙角容易发生塑性变形和损伤,引发巷道变形开裂甚至混凝土块塌落、墙角底板翘起出现裂缝等破坏现象,由于地下巷道工程地质背景的复杂性,对于巷道发生的破坏类型,需要根据巷道的实际破坏现象及工程背景进行分析计算,来保证计算的可靠性。
(3)地震发生初期,巷道的墙角底板破坏明显强于墙角立板,可能会发生墙角立板破裂引发巷道腰部立板倾斜下沉,造成巷道塌落,导致巷道产生整体失稳破坏。


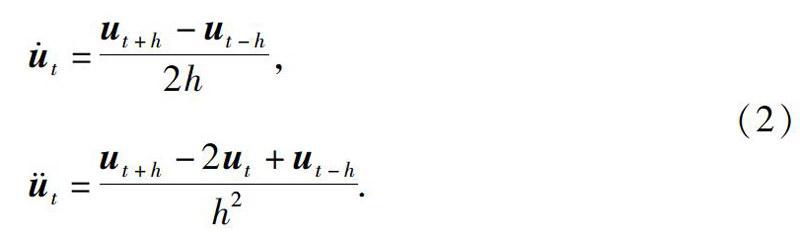
摘要:为研究煤矿地下巷道在地震作用下的动力响应,考虑巷道结构的损伤效应,基于显式算法的土结构体系动力学方程,建立ANSYS/LS-DYNA三维数值模型,并在模型指定位置设置观测点。通过观测点的动力响应特征研究巷道的动态响应。结果表明:巷道在地震作用下,半拱形巷道应力主要分布在拱帮和墙角立板、底板处,且拱帮和墙角处塑性体积应变明显,巷道墙角处的损伤明显大于其他各部,是巷道容易发生破坏的部位。
关键词:地下巷道;动力响应;有限元分析;地震作用;ANSYS/LS-DYNA
中图分类号:TD32 文献标识码:A 文章编号:1000-0666(2016)01-0022-06
0 引言
近年来,随着我国煤炭资源开采的增多,我国煤矿区形成了大量形式各异、大小功能不同、纵横交错的地下巷道。我国80%的矿区处于地震多发区,由于缺少完善的地下结构抗震设计规范,巷道在地震作用下的稳定性值得我们关注,因此研究巷道的地震动力响应特征及其变化规律十分必要。孙超等(2009)已经对地下结构的动力稳定性问题做了大量研究:刘晶波等(2005)对地铁盾构隧道的地震响应进行了数值分析;刘书贤等(2013)研究了煤矿采动与地震耦合作用下建筑物灾变机理;章泳健等(2010)基于LS-DY-NA研究了隧道的初应力计算方法;姜耀东等(2005)分析了放炮震动引发煤矿巷道动力失稳的机理;高富强等(2009)分析了动力扰动下巷道围岩力学响应。
对于地下结构的研究比较多的是对地铁等浅埋结构的研究,但对于地震作用下巷道响应的研究较少,且考虑因素单一,对于巷道结构在地震中的损伤(赵宝友,2009)、岩层分布及其与巷道的接触和波动效应未给予充分的考虑。本文针对煤矿开采地下巷道在初始应力场和地震共同作用下巷道的地震响应研究的不足,基于ANSYS/LS-DYNA的显式动力有限元模型,考虑巷道在地震过程中的损伤及巷道与围岩的接触效应,在模型边界设置无反射边界,对煤矿采煤地下巷道进行了三维数值地震动响应分析研究。
1 巷道围岩-结构体系动力有限元分析
由于巷道结构与围岩之间存在相互作用,在分析巷道围岩体系结构的同时还要对结构围岩进行分析。围岩作为一种半无限介质,在数值计算中一方面主要是通过引入人工边界(如粘性边界、粘弹性边界等)模拟连续介质的辐射阻尼,保证散射波能量从有限区域穿过人工边界(何伟,2011)。另一方面是模拟围岩的非线性,本文考虑围岩材料非线性和接触非线性,围岩采用D-P理想弹塑性模型,就可以很好地描述围岩的非线性行为。
1.1 巷道围岩-结构体系动力方程
根据达朗贝尔原理可以建立该体系地震动作用下任意时刻有限元平衡方程(克拉夫,彭津,2006):
Mü+Cu+Ku=P. (1)式中,M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,P是节点荷载向量;u、u、ü分别是体系的位移、速度和加速度。该运动方程一般将整个地震过程分成若干微小时间段h,假设体系在微小时间段内体系是线性变化的,然后采用直接积分法解得,LS-DYNA采用显式中心差分法,即:
阻尼采用Rayleigh阻尼,它是将结构整体阻尼矩阵C表示成整体质量矩阵M和整体刚度矩阵K的线性组合:C=αM+βK,式中比例常数α和β阻尼系数可以由振型阻尼比计算得到,在LS-DYNA中通过关键字:*DAMPING设置(ISCT,2007)。
2 地震作用下巷道-围岩动力失稳演化分析
2.1 有限元分析模型
建立三维有限元模型,模型尺寸为y向610m,X向660m,Z向300m;岩层和巷道物理力学性能如表1,岩层分布如表2。巷道为半拱形巷道,拱直径4m,巷道的纵向长度为200m,衬砌厚度为400mm。围岩和巷道衬砌使用solid164体单元,人工边界采用无反射边界。岩层材料采用理想弹塑性DP材料,巷道结构采用C50混凝土,LS-DYNA中通过*MAT_072113材料模型实现巷道损伤本构。
2.2 地震波的选取与调整
国内外研究表明,选取地震波需满足强度、频谱特性、波的持时的要求,不同地震波参数得出的地震响应可能相差明显,因而选择合理的地震波参数进行动力分析是必要的。本文选用了15s的El Centro地震波,最大加速度调整为150cm/s2,如图2所示,地震波在基岩底部沿X水平输入。
2.3 数值模拟结果分析
在巷道100m处截取截面,并在截面不同部位设置观测点,如图3所示。
2.3.1 巷道应力分析
图4为巷道应力的典型分布图,从图中可知,巷道的等效应力和S1主要分布在墙角和拱帮偏下,S3主要分布两侧拱腰处;最大剪应力在墙角处最大,拱帮偏下处次之;这说明巷道的墙角立板和拱腰处成了高应力集中区。
图5为巷道取100m纵深截面时不同部位的最大应力(等效、S1、S3、剪应力),由图可知,等效应力、S3和最大剪应力的峰值在左右拱帮偏下的位置(5、6、7、26、27、28号点)和墙角立板的位置(12、13、20、21号点);S1峰值在左右拱帮偏下(8号点)和左右立板腰部(10、11、22、23号点)位置;这说明巷道的拱帮偏下和墙角是拉、剪复合最大应力区,巷道的立板腰部主要受拉应力作用;地震作用下的高应力反复的加、卸载会对巷道的这些部位造成较大破坏,对于在拉、剪复合应力区的拱帮和墙角破坏更明显,墙角处尤其明显。
2.3.2 损伤分析
图6为巷道的塑性体积应变,从图中可知巷道拱帮发生了明显的塑性体积应变,且由巷道中部向巷道两端扩展时,巷道的塑性体积应变有减小的趋势,但是在巷道的两个端部又有所增大,造成巷道两端塑性体积应变有所增大的主要原因是端部边界条件不同;其次在巷道内侧的墙角处也出现了明显的塑性体积应变,在巷道发生塑性体积应变的部位(巷道帮部、腰部至墙角立板)积累了明显的损伤,这些损伤使得巷道在这些部位更容易遭到破坏。
图7为巷道取100m纵深截面时不同部位的最大塑性体积应变,由图可知,巷道的左右帮部(5、28号点)和墙角底板(13、20号点)的塑性体积应变最为明显,这说明巷道的左右帮部和墙角底板会发生相对于其他部位更明显的变形,这可能造成帮部开裂、墙角底板翘起,同时伴随着小块石飞溅。由于巷道的墙角立板(13、21号点)和帮部偏上(5、28号点)的塑性变形较为明显,因此在这两处积累损伤较为明显,其中墙角底板损伤尤为严重,这说明在地震作用过程中,墙角立板在拉、剪应力反复作用下会积累大量的损伤,拱帮偏上损伤程度也要明显大于其他部位,这会造成墙角立板和拱帮偏上处最先发生破坏,随着这种破坏的扩展,就可能引发立板和上帮失效,进而引发整个巷道的破坏。
2.3.3 时程分析
由上述可知,地震作用过程中巷道的墙角处应力最为复杂,变形最为明显。本节提取了巷道墙角12和13号观测单元的应力和塑性体积应变的时程曲线。分析图8的巷道墙角立板和底板的应力时程曲线可知:巷道墙角的应力在t=2s和f=8s会出现两个峰值,在基道取100m纵深截面的前提下,t=2s时的应力峰值与输入加速度的峰值时刻基本一致,t=8s的应力峰值较加速度峰值有所提前;巷道墙角立板的等效应力在整个时程中小于墙角底板的等效应力,S1应力的墙角立板的应力大于底板的应力,S3应力中间时刻较为明显,最大剪应力墙角底板在整个过程中基本大于立板。
图9为巷道墙角的塑性体积应变时程曲线。由时程曲线可知立板和底板的塑性体积应变变化基本一致,底板的塑性体积应变大于立板的,从而使得底板的损伤大于立板。故可得出在整个地震过程中,半拱形巷道的墙角底板应作为抗震的重点防护部位。
3 结论与讨论
本文基于显式动力有限元理论,分析研究了地震作用下地下巷道结构动力响应及其损伤破坏,利用ANSYS/LS-DYNA建立了地下巷道地震作用下的三维计算模型,通过有限元分析计算得到如下结论:
(1)地震作用下巷道结构的拱帮和墙角处会出现周期性高应力集中区域,在墙角处会出现拉、剪同时达到最大,说明了半拱形巷道的拱帮和墙角最容易发生动力破坏,在巷道的拱帮偏下和墙角处会发生明显的塑性变形以及发生较严重的损伤,需要重视对巷道结构拱帮和墙角的设计,同时也要及时进行加固维护,以保证巷道结构的安全使用。
(2)地震动力荷载作用下巷道的拱帮和墙角容易发生塑性变形和损伤,引发巷道变形开裂甚至混凝土块塌落、墙角底板翘起出现裂缝等破坏现象,由于地下巷道工程地质背景的复杂性,对于巷道发生的破坏类型,需要根据巷道的实际破坏现象及工程背景进行分析计算,来保证计算的可靠性。
(3)地震发生初期,巷道的墙角底板破坏明显强于墙角立板,可能会发生墙角立板破裂引发巷道腰部立板倾斜下沉,造成巷道塌落,导致巷道产生整体失稳破坏。

