《浅谈数学词汇与古代车马的渊源》-理学论文，数学论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

浅谈数学词汇与古代车马的渊源

范文

王继强范甜

【摘要】结合自身教学经验和科研实践，从古代车马构造的角度对数学中一些重要词汇的由来给出了解读，以求达到追根溯源、解疑释惑之目的.

【关键词】古代车马;数学词汇;渊源;轮;轴;辐;鞍

【基金项目】山东财经大学首批通识选修课核心课程项目资助.

一、引言

车的发明是人类文明和进步的重要标志.中国是世界上最早使用车辆的国家之一.从新石器时代晚期的奚仲造车，到古代畜力车，到近代人力车，再到现代汽车的普及，都说明车辆在人类社会发展进程中的重要意义.

小而言之，古代车马极大地丰富了汉语的词汇宝库，比如，“南辕北辙、肩负重轭、螳臂当车、学富五车、车水马龙、舟车楫马、香车宝马、逸闻轶事、云程发轫、柔远绥怀、毂交蹄劘、冯轼结靷”等成语无不与车马有关.更小而言之，古代车马甚至与数学也有密不可分的关系.本文试图从若干数学词汇的来源角度来揭示这些关系.

二、渊源例释

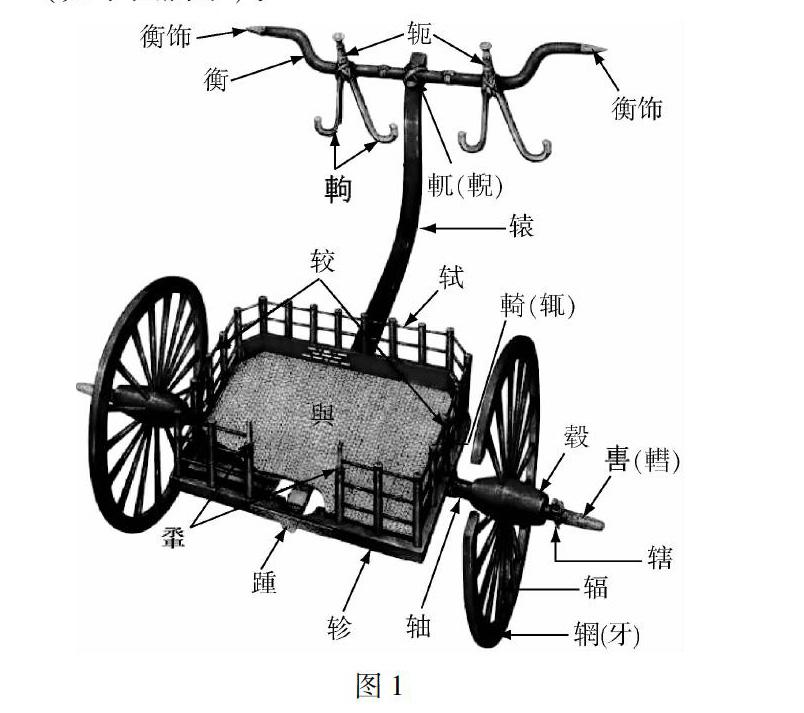
下面是笔者根据资料整理绘制的古代车马的基本结构图[1，2]（如下图所示）：

图1

（一）轮

在古代车马中，“轮”（wheel）无疑是一个极其关键的组成部分，其构成要件主要有轴、辐、毂、辖、辋等（如图1所示）.在数学上，“轮”是图论中的一种图（graph），其定義如下：A wheel is a graph obtained from a cycle by adding a new vertex and edges joining it to all the vertices of the cycle.[3]易见，图论中的“轮”与古代车马中的“轮”是何其相似！

（二）轴

在古代车马中，轴（axis）是穿在车轮中间的圆柱形物件（如图1所示）.在数学上，有许多“轴”的概念.比如，直角坐标系中的坐标轴（coordinate axis）、极坐标系中的极轴（polar coordinates）;再比如，如果一个平面图形沿着一条直线折叠后，直线两侧的部分能够互相重合，则称该图形为轴对称图形（axial symmetric figure），该直线称为对称轴（symmetry axis）.易见，数学上的“轴”像极了古代车马中的“轴”！

（三）辐

在古代车马中，“辐”（spokes）是插入轮毂以支撑轮圈的细条（如图1所示）.“辐”密集地聚集在轮毂中，所以汉语中“辐集、辐聚、辐辏、辐射”等词语都有“聚集”之意.在复数的三角形式中，设复数z=a+bi（a，b∈R）对应的向量为OZ，则以x轴的正半轴为始边、射线OZ为终边的角θ称为复数z的辐角（argument）[4].显而易见，当点Z沿逆时针方向移动时，各辐角的终边恰恰呈现出“辐”的形象.

此外，在图论中，“辐”是也“轮”的一部分，其定义如下：A wheel is a graph obtained from a cycle by adding a new vertex and edges joining it to all the vertices of the cycle.The new edges are called the spokes of the wheel.[3]

（四）鞍

在古代车马中，鞍（saddle）是套在马背上便于人骑坐的用具.在数学上，马鞍面（saddle surface），也称为双曲抛物面，是三维空间中一种常见的曲面，其函数解析式为z=x2a2-y2b2（a，b>0）.易见，马鞍面恰恰是“鞍”的表面形状的真实写照.此外，与“鞍”有关的数学词汇还有“鞍点”（saddle point），如（0，0）是函数y=x3的鞍点，（0，0，0）是函数z=x2-y2的鞍点等，其命名也是来自“鞍”的形状特征.

（五）轭

在古代车马中，“扼”（yoke）是套在马肩膀上的曲木（如图1所示）.“共扼”，顾名思义，是指两匹马共套用一个轭，以使其同步行走.《圣经·新约》有云：“信与不信，不能同负一轭”，即此意也.在复数理论中，实部相同、复部互为相反数的两个复数z1=a+bi，z2=a-bi（a，b∈R）称为共轭复数（conjugate complex number）[4].显而易见，在直角坐标平面上，共轭复数对应的两个点恰好关于实轴对称，就好似两匹马的肩膀上共架一个“轭”（实轴），并行拉一辆车.这就是“共轭复数”一词的由来！

（六）轼

在古代车马中，“轼”（crossbar）是车厢前面用作扶手的横木（如上图所示）.当车子颠簸时，乘车人必须紧紧抓住“轼”，才能够保证安全，故“轼”通“式”，引申为“规范、标准”.在数学上，称为“式”的词汇很多，比如，“公式”“恒等式”“解析式”“一般式”“范式”等的“式”都含有“规范、标准”的意思.

（七）轨

在古代车马中，“轨”（trail）是两车轮之间的距离，后引申为“辙”，路线之意也.秦时“书同文，车同轨”指的就是要统一文字和“轨”的大小.在图论中，“轨”是图中的一种构造，其定义如下：A walk inG is a finite non-null sequence W=v0e1v1e2…ekvk whose terms are alternatively vertices and edges，such that for 1≤i≤k，the ends of ei are vi-1 and vi.If the edges of a walk W are distinct，W is called a trail.[3]简言之，“轨”就是图中的一条点和边交错出现，且边不重复的路线，这与古代车马中“轨”的引申义是完全一致的.

三、结束语

以上，笔者从古代车马的构造角度，对数学上的几个词汇的来龙去脉进行了初步探究.这样的探究对深入理解相关概念显然是十分有益的.我们相信，数学上还有很多类似的问题值得我们去探究.

【参考文献】

[1]周成.中国古代交通图典[M].北京：中国世界语出版社，1995.

[2]吴迪.古代车马[M].长春：吉林文史出版社，2010.

[3]Bondy J.A.，Murty U.S.R.Graph theory with applications[M].London and Basingstoke：The MacMillan press，LTD，1976.

[4]人民教育出版社数学室.代数（下册）[M].北京：人民教育出版社，1990.

[5]同济大学数学系.高等数学·下册（第六版）[M].北京：高等教育出版社，2007.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。