《中国国际贸易进口ARIMA季度模型》-管理学论文，决策论文-论文范文参考-科学狗论文网

标题

中国国际贸易进口ARIMA季度模型

范文

李卓+谢沅潮

【摘要】中国国际贸易进口一直以来是推动我国经济增长的重要因素，国际贸易进口有其自身的发展规律。本文通过采用Eviews7.2软件的自回归平均移动季度模型（ARIMA模型），对中国国际贸易进口月度数据（从2012年11月到2016年02月期间）进行一个季度性的静态预测拟合。根据所拟合的中国国际贸易进口数据的拟合度可以得出，中国国际贸易进口数据的上半年的季度模型所拟合的数据相对偏差率在5%左右，而下半年所拟合的中国国际贸易进口季度模型的数据与实际进口数据的相对偏差率在10%左右。因此，可以判断中国国际贸易进口数据的上半年季度模型（即前两个季度的ARIMA模型）的拟合度要高于下半年的季度模型。对中国国际贸易进口数据的拟合和预测，采用上半年的季度ARIMA模型进行拟合更加贴近实际数据。

【关键词】中国国际贸易进口数据；自回归移动平均模型；季度模型

一、引言

在英国古典经济学家亚当.斯密（Adam.Smith）的代表著作《国富论》中，著名的”看不见之手”的机制理论，是国际贸易发展的一个最早的代表性理论。该机制中，亚当.斯密提出，社会各个经济主体按自己所擅长的专业进行分工，然后采用专业化生产，通过市场进行交易，实现社会福利最大化。然而，当交易活动一旦越出本国范围，国际分工和国际贸易就出现了。亚当.斯密的这一理论被称为绝对优势理论。之后，英国古典经济学家大卫.李嘉图（David.Ricardo）突破了亚当.斯密的绝对优势理论，提出了比较成本原理，奠定了近代比较优势学说的基础。比较优势理论的创立，带动了西方学者对国际贸易理论研究的第一个高潮。之后，新古典贸易理论学家俄林（Olin）在其代表作《区域贸易和国际贸易》中提出了要素资源禀赋理论。古典和新古典国际贸易理论中，国际贸易在价格的比较和竞争下，推动了一个国家的进口和出口，从而促进了一个国家的专业分工以及商品的专业化生产。因此，对国际贸易的进口和出口的研究有助于我们更好的了解国际贸易发展的规律。

自从中国改革开放以来，中国国际贸易获得了飞速的发展，特别是在扩大内需的政策指引下，中国国际贸易的进口额得到了很大的提升，到2015年止贸易进口总额10.45万亿元，对国民经济的发展起了推动作用。郝雁（2005）采用ARMA最优预测模型对中国进出口与经济增长进行了相关性分析，采用了单元自回归平均移动模型的小样本最优预测模型建模，拟合了中国进出口与经济增长之间的关系及原因，提出国际贸易与经济增长之间呈现出显著的正相关关系，并认为中国适度增加进口规模以提高中国出口的竞争力和促进中国产业结构的升级。张帆、蓝丹阳（2015）使用ARMA模型对广西进出口总额时间序列预测，提出以进出口的提升来带动经济的发展。敬久旺（2011）采用ARMA乘积季节模型对我国海关进出口商品总值进行了季节性拟合，采用频域分析法和时域分析法对中国海关进出口商品总值进行分析。沈汉溪、林坚（2007）采用季节性ARMA模型对中国外贸进出口的总额及出口总额和进口总额的实际值进行了预测。雍红月、包桂兰（2008）采用组合时间序列ARMA模型对内蒙古的GDP进行了预测。

二、数据来源

本文采用中国2012年11月至2016年02月的国际贸易进口数据，对中国进口贸易进行一个向量自回归平均移动模型分析，即拟合中国国际贸易的贸易进口ARMA模型。对中国国际贸易进口数据进行一个统计分析后可以得出，2012年11月至2016年02月期间中国国际贸易的进口额均值为1533.787（亿美元），中间值1584.240（亿美元），其中偏度-0.93，峰度3.7，呈现出一个‘高瘦、左拖尾的趋势，JB值6.69（0.03）在0.05的置信度下不服从正太分布。从数据的趋势可以看出中国贸易进口额大体上分别分布在2012年11月至2014年12月，和2015年01月至2016年02月这两个时间区间，其中2012年11月至2014年12月期间的国际贸易进口额的平均数额高于2015年01月至2016年02月的国际贸易进口平均数额。两段时间趋势都呈现出季节性波动，从2012年11月至2014年12月期间的波动呈现出1至2个季度的波动周期，而在2015年01月至2016年02月期间的进口波动呈现出1个季度的波动周期。在2014年12月期间以后，中国国际贸易进口额大幅度下滑，后平稳在1400（亿美元）的均值线的2015你01月至2016年02月的贸易进口阶段，如图一所示。

三、数据检验和调整

（一）数据检验

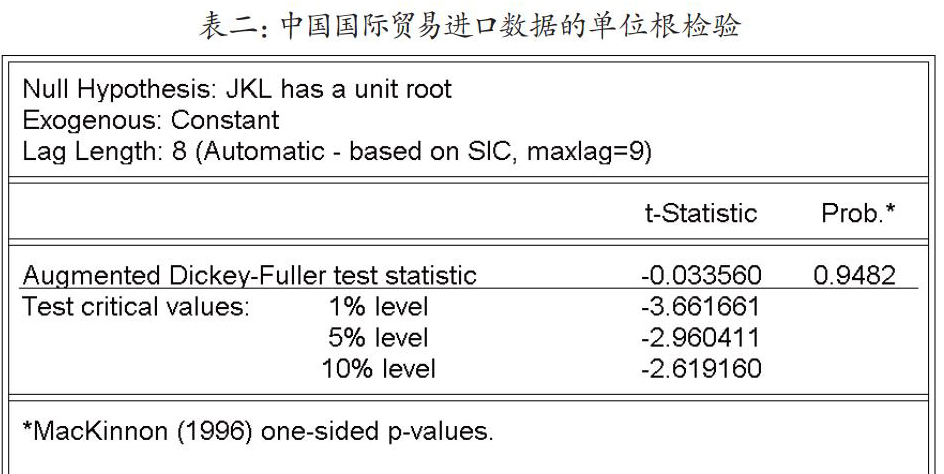
对中国的2012年11月至2016年02月中国国际进口的月度数据进行相关性分析可以得到表一的向量的自相关性检验数据和偏相关性检验数据，其中进口数据在其一阶、三阶和十二阶滞后期处存在自相关性，并存在一阶、三阶及八阶滞后期的偏相关。这说明中国国际进口数据存在一阶和三阶的自相关以及高阶自相关。接着，我们对中国国际贸易进口数据进行滞后8阶的ADF单位根检验，得到表二的单位根检验结果，t统计值-0.033560（0.9482），t值大于置信区间在1%、5%和10%的t统计值（参见表二）。所以，我们不能拒绝零假设，即说明中国国际进口数据中存在单位根，数据不是一个平稳的数据。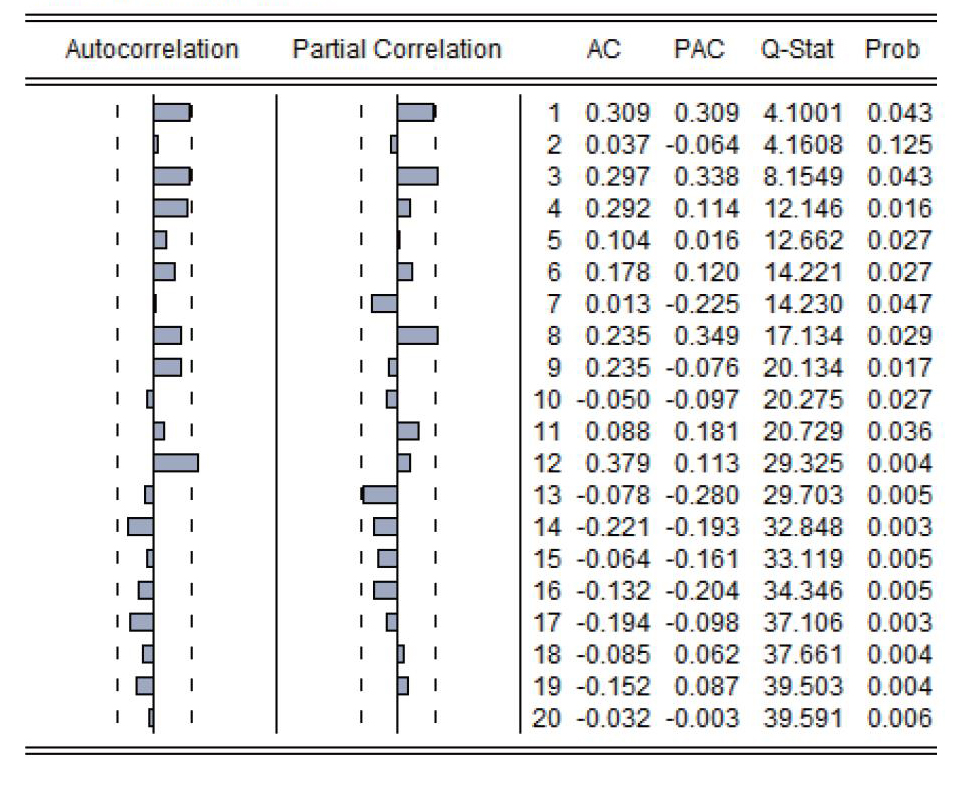

（二）中国进口数据季度调整

根据中国国际进口数据的自相关性检验分析以及单位根检验的分析数据，我们可以得出中国国际贸易的进口数据有1、3、12阶的自相关性以及1、3、8阶的偏相关，说明该数据存在一个季度性的自相关性。因此，我们对中国国际贸易2012年11月至2016年02月的进口月度数据进行一个季度高频数据转换，得到中国国际贸易进口的季度数据。为了减少该数据的波动性，我们对该数据进行一个对数变换处理和差分变化处理，得到了中国国际贸易进口季度数据的对数变化及差分变化后的数据。

进行对数变化以及差分变化后的中国国际贸易进口数据，均值为-0.009528，中值为0.014511，最大值是0.086289，最小值是-0.240803，标准差是0.083788，偏度为-1.820209，峰度5.991976，JB统计值为11.10228（P值0.003883）。对数差分贸易进口数据满足零均值的假设，数据偏度小于零存在向左偏移的分布，峰度大于三存在‘瘦高尖峰的分布，JB统计P值接近于零而小于0.05的置信水平，因此，我们拒绝正太假设的分布的原假设。

接下来我们对中国国际贸易进口季度对数差分数据进行自相关性检验和单位根检验，得到表三和表四的检验结果。从自相关性检验检验结果和单位根检验结果中，数据的自相关分布和偏相关分布都位于两倍置信区间之内，而其P值基本上大于0.05的置信水平，白噪声显著，因此，我们可以得出中国进口季度对数差分数据不存在自相关和偏相关性，如表三所示。然后从我们对该数剧进行滞后二阶的ADF单位根检验结果，如表四的检验结果即滞后二阶的单位根检验的t值水平等于-3.762088（P值等于0.0198），大于1%的置信水平下的P值即-4.200056，因此，我们可以接受滞后二阶的对数差分进口数据不存在单位根的假设。由此，我们可以得出，中国国际贸易进口季度对数差分数据在1%的置信水平下不存在单位根的结论，即可以得出在1%的置信水平下中国国际贸易进口对数差分数据是一个平稳数据。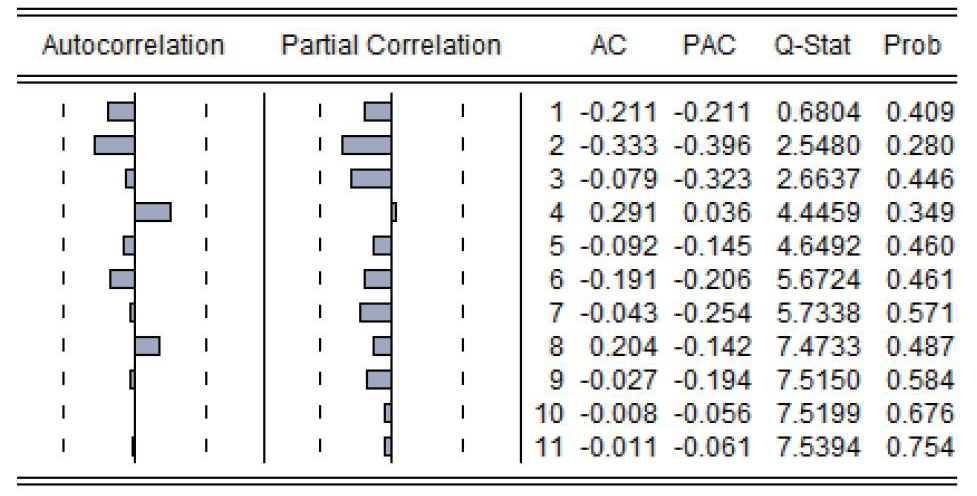

同时我们还可以从中国国际贸易进口数据描述统计中可以看出，对数差分变化后的中国国际贸易进口数据基本上分布在0.00值左右的（-0.10，0.10）的区间范围，只有1个季度的数据分布在（-0.25，-0.20），在（-0.10，-0.05）区间有两个季度的数据，在（-0.05，0.0）区间和（0.05，0.10）区间有1个季度数据，而在（0.00，0.05）区间分布有七个季度数据，即有81.8%的对数即差分变化后的季度数据分布在（-0.10，0.10）这个区间，满足了我们减小数据波动和数据变化稳定的目的。而根据对数差分变化后的中国国际贸易进口数据的折线图我们可以看出，出现在（-0.10，0.10）区间之外的数据是来自2015年的第一和第二季度，因此，我们可以看出2015年第一、二季度是偏离样本均值范围比较明显的期间，对样本影响存在比较明显的波动。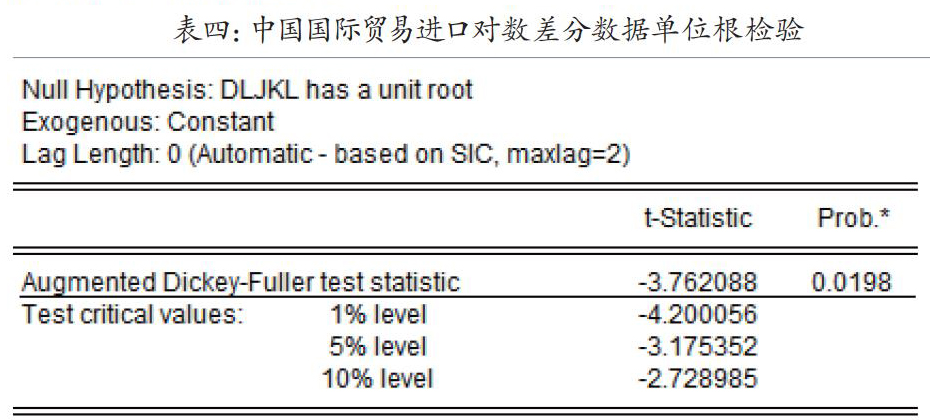

四、模型设置

（一）ARMA模型

ARMA模型是一种建立在时间序列分析的基础上对产生的误差项用博克斯-詹金斯法建立误差序列模型。博克斯-詹金斯B-J方法或ARMA方法，是一种时间预测方法，它将预测对象随时间变化形成的序列看作是一个随机序列，时间序列依赖于时间T的随机变量，序列变化的不确性可以用一定的规律性方法进行描述，即可以采用ARMA等模型进行近似的描述。这种规律性的发展用ARMA模型描述出来之后，就可以对时间序列的规律性进行一个过去值和现在值得预测和拟合。ARMA模型的构建是依据时间序列变量的滞后值以及当期值的相互关系，进行的一个变量滞后关系的数量建模，其中变量的滞后期数要根据时间序列的自相关以及偏相关的滞后期数来进行滞后阶数的确认，然后进行ARMA模型的滞后阶数的回归拟合。

我们对中国国际贸易进口数据进行一个ARMA变量自回归平均移动模型建模，其中根据对中国国际贸易进口额的一个数据统计描述分析，得出中国国际贸易进口数据是一个时间序列变量。该数据在2012年11月至2016年02月期间随季节性的波动比较显著，因此，我们可以采用一个时间序列模型对该数据进行一个自回归的拟合。

（二）ARIMA模型

对于季度数据的建模，我们进行变量自回归移动平均估计时，可以采用ARMA季度模型即ARIMA模型。ARIMA模型要求估计时，对于非季度回归时变量自相关滞后p阶采用ar（p）项，偏相关平均移动非季度项采用ma（q）项，并且可以对变量进行d阶差分调整，以进行季度数据的调整。对于季度性回归时，可以根据季度向量自相关滞后P阶采用sar（p）项进行拟合，平均移动Q阶项可以采用sma（q）项进行拟合，并可以进行季度差分调整D阶。

五、模型估计

我们现在利用调整后的中国2013年第一季度到2015年第四季度国际贸易进口数据，进行一个自回归估计，构建一个ARMA季度模型，即ARIMA模型。根据中国2013年第一季度到2015年第四季度国际贸易贸易进口的季度数据的调整，中国国际贸易进口数据的自相关系数在一阶、三阶及十二阶超出两倍的检验置信区间，存在自相关的关系，可以采用非季度自回归AR（2）的滞后回归，并且滞后回归在第四期也接近2倍置信区间整体可以看出呈现一个季度性的相关性我们则在季度回归项采用SAR（1）项进行季度自回归拟合。对于平均移动项，我们可以根据变量偏自相关系数在第一阶、三阶、八阶的偏相关性，采用非季度移动项的MA（2），及根据第八阶的偏相关系数的相关性采用季度的移动项SMA（4）的一个模型回归。模型估计形式为ARIMA（2，1，2）（1，1，4），即采用1-4模型形式对中国国际贸易进口数据进行一个季度回归估计，模型估计的结果为

之后我们对ARIMA（1，1，2）（2，2，4）模型进行残差拟合优度检验、自相关检验及1阶LM序列相关白噪声检验。其中中国国际贸易季度ARIMA模型的残差检验数据均分布在二倍置信区间之内，残差的拟合优度比较高通过检验。在进口数据自相关检验中，自相关系数和偏相关系数均在置信区间之内，白噪声序列在0.01置信水平通过检验。在LM序列相关检验中，P值高于1%、5%和10%的置信度。通过相关检验之后，我们进行ARIMA模型的数据动态和静态拟合，其中平均相对误差百分比值即MAPE值为95和157.4数值偏大，拟合度不够高，同时调整后的R-square系数为0.72数值偏低，如图二所示。因此，我们对中国国际贸易进口季度ARIMA模型再次进行一个参数调整。

根据中国国际贸易进口对数和差分变化后的数据，中国国际贸易进口对数差分变化后的数据在2015年第一和第二季度偏离零均值样本范围比较显著，是影响该数据变化的主要时期变化区域，因此，我们考虑从该区域的数据变动趋势中构建一个两个季度的中国国际贸易对数差分变化后的进口季度ARIMA模型。同时，根据中国国际贸易进口数据的季度性特征即其自相关的滞后阶数的特征，我们分别引入季度虚拟变量q1、q2、q3和q4，分别拟合各个季度之间的相互关系，即构建一个中国国际贸易进口ARIMA季度虚拟变量模型。由于季度数据的自由度限制以及单位根检验的效果，对中国国际贸易进口数据的季度虚拟变量的整体拟合即（q1、q2、q3和q4的同时回归估计）和单个季度数据的拟合即q（i）（i=1、2、3、4）的拟合效果不够高，因此，我们只能采用分别对前两个季度的即半年期的虚拟变量（q1和q2同时拟合）的模型进行估计，和后两个季度的即后半年的虚拟变量（q3和q4同时拟合）的模型进行估计。

F=658.6307 AIC=-8.04 SC=-7.89027，DW=2.2995其中模型2-1是含有第一、二季度项的均值方程模型，模型2-2是中国国际贸易进口第一、二季度自回归平均移动模型。其中在均值方程模型中第一季度的影响系数0.2717，比第二季度的影响系数0.087要高，第一季度的影响要更加显著。ARIMA模型的自回归滞后项为1阶，移动项为2阶。变量自回归方程系数分别-0.6363和季度项系数-0.086，说明非季度项的影响要更加显著。而对于平均移动项，非季度移动项0.2646、季度移动项系数为-0.99，季度移动项系数更加显著，同时移动项采用的是一个二阶差分项。方程模型2-2的整体拟合优度R-squared系数为0.9994，调整后的R-squared系数为0.9979。方程整体拟合优度较高，但是F值偏高，DW值接近2。方程整体拟合得比较理想。

F=35.972 AIC=-5.144 SC=-4.99，D.W=2.229293，模型2-3是含有第三、四季度项的均值方程模型，模型2-4是中国国际贸易进口第三、四季度自回归平均移动模型。从方程模型2-3的回归系数中我们可以看出第四季度对中国国际贸易进口存在负向作用，而第三季度数据系数为0.2517比较显著。在方程模型2-4中，非季度变量自回归项系数为1.088，季度变量自回归项系数为0.24，非季度变量自回归项系数显著，变量自回归项为2阶差分项。非季度性平均移动项系数为0.99，季度平均移动项系数为-0.99，非季度平均移动项系数比较显著。方程R-squared系数为0.9908，调整后的R-squared为0.9632，F值35.972，DW值为2.2292，方程整体拟合理想。

从两个回归方程的拟合结果及参数来看，两个方程的拟合程度很高.接下来我们对两个方程进行残差的拟合检验、自相关检验以及LM序列相关检验。检验结果分别如下表中显示，两个方程的残差拟合检验通过，残差位于检验的置信区间里，自相关检验通过，自相关系数和偏相关系数分别位于两倍置信区间内，序列为白噪声，LM检验通过，置信度超过1%、5%和10%，序列不存在自相关，中国国际贸易进口季度虚拟变量ARIMA模型拟合的方程性程度比较高。

六、模型预测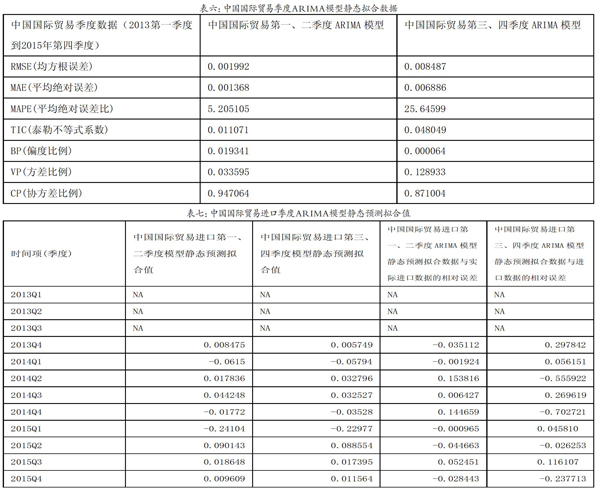

Eviews7.2软件的静态预测采用的是滚动向前的预测方法，即拟合一次数据后在估计区间采用真实值替代拟合值再做向前一步的拟合。对于ARIMA季度模型采用真实值进行预测拟合比较准确。我们现在分别采用静态预测对中国贸易进口ARIMA第一、二季度模型和第三、四季度模型，进行中国贸易进口数据进行静态预测拟合。得到拟合结果如下，ARIMA季度模型的第一、二季度静态预测模型的均方根误差0.001922、平均绝对误差0.001365、平均绝对误差率5.205105、泰勒不等系数0.011071、偏差比0.019341、方差比0.033595和协方差比0.947054。ARIMA季度模型的第三、四季度静态预测模型的均方根误差0.008487、平均绝对误差0.006885、平均绝对误差率25.64599、泰勒不等系数0.048049、偏差比0.000064、方差比0.128933和协方差比0.871004.以及拟合静态预测统计表如下，从两个静态拟合表来看采用第一、二季度数据拟合的预测曲线的两倍置信区间更加准确，拟合效果比第三、四季度模型好。然后我们采用两模型的拟合数据与中国2013年第一季度到2016年第四季度的贸易进口数据进行比较得到如下数据统计表，第一、二季度模型的拟合数据比较接近实际数据，并且对第一、二季度拟合数据和第三、四季度拟合数据进行一个实际数据的相对误差率的计算得到每个季度数据的静态预测数值与实际数值之间的相对误差率，可以看出第一、二季度模型预测数据误差率在0.05左右，第三、四季度模型预测数据误差率在0.1左右。因此，中国贸易进口ARIMA季度模型的第一、二季度模型的静态预测拟合效果更好，该模型所做的拟合效果更加接近实际数据的变化规律。因此，我们对中国国际贸易进口数据的预测和拟合时，采用上半年的季度回归ARIMA模型进行的数据拟合，要更加贴近实际数据，拟合效果比较理想。

参考文献

[1]樊欢欢，李嫣怡，陈胜可.赢在职场第一步-Eviews统计分析与应用[M].机械工业出版社，2011：7.1.

[2]沈汉溪，林坚.基于ARIMA模型的中国外贸进出口预测：2006-2010[J].国际贸易问题，2007（6）.

[3]敬久旺.基于ARIMA乘积季节模型的我国海关进出口商品总值的时间序列分析[J].技术与市场，2011（7）.

[4]郝雁.中国的进出口与经济增长：ARMA最优预测模型分析[J].统计观察2005（2）.

作者简介

李卓（1969.6—），男，汉族，湖北应城人，中国共产党党员，学历：研究生，经济学博士，现任世界经济系主任、博士生导师。

谢沅潮（1980.9月—），男，壮族，广西南宁人，武汉大学世界经济系在读研究生。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。