《空间机器人机械臂避障工作空间的研究》-管理学论文，企业管理论文-论文范文参考-科学狗论文网

标题

空间机器人机械臂避障工作空间的研究

范文

李亚云张大伟

【摘? 要】避障工作空间（obstacle avoiding planning workspace，缩写为OAPW，简称避障空间）的研究是机器人路径规划过程中一个至关重要的问题。论文首先利用DH参数建立了空间机器人机械臂，其次工作空间与障碍物的模型建立采用了蒙特卡罗方法。然后描述了避障工作空间建立的方法。最后，仿真出三维空间内的避障空间模型。

【Abstract】Research on obstacle avoiding planning workspace （abbreviated as OAPW） is a crucial issue in robot path planning process. This paper firstly establishes the space robot robotic arm by using the DH parameter. Secondly， Monte Carlo method is used to establish the model of the working space and obstacles. Then， this paper describes the method of establishing obstacle avoidance workspace. Finally， this paper simulates the obstacle avoidance space model in three-dimensional space.

【关键词】操作臂;工作空间;避障空间;路径规划

【Keywords】operation arm; working space; obstacle avoidance space; path planning

【中图分类号】TP242? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文献标志码】A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文章编号】1673-1069（2020）05-0163-03

1 引言

机器人机械臂末端可达到的点构成了工作空间，记作WR，表示为：

WR={p（q）：q∈Q}？奂Rn? ?（1）

式中，运动学正解的坐标信息由p（q）：q∈Q→Rn反映出，Q反映的关节空间信息，Rn则反映出二或三维空间，q反映的关节变量。

避开障碍物的规划研究的方法分为两种：其一直接把障碍物转化为约束条件;其二将工作空间内存在的障碍物剔除获得避障空间。

避障工作空间表示为：

WI={p（qc）∈WS∩OBS}？奂Rn （2）

式中，WI表示相交空间，OBS表示障碍物，n=2或3，Rn表示二或三维空间;qc是笛卡尔坐标。

现有的计算工作空间的类型大体有数值法、几何法和解析法[1]，常采用的数值法通常是基于Monte Carlo的方法，主要原因是通用、简便，工程应用最为广泛[2]。

2 机械臂

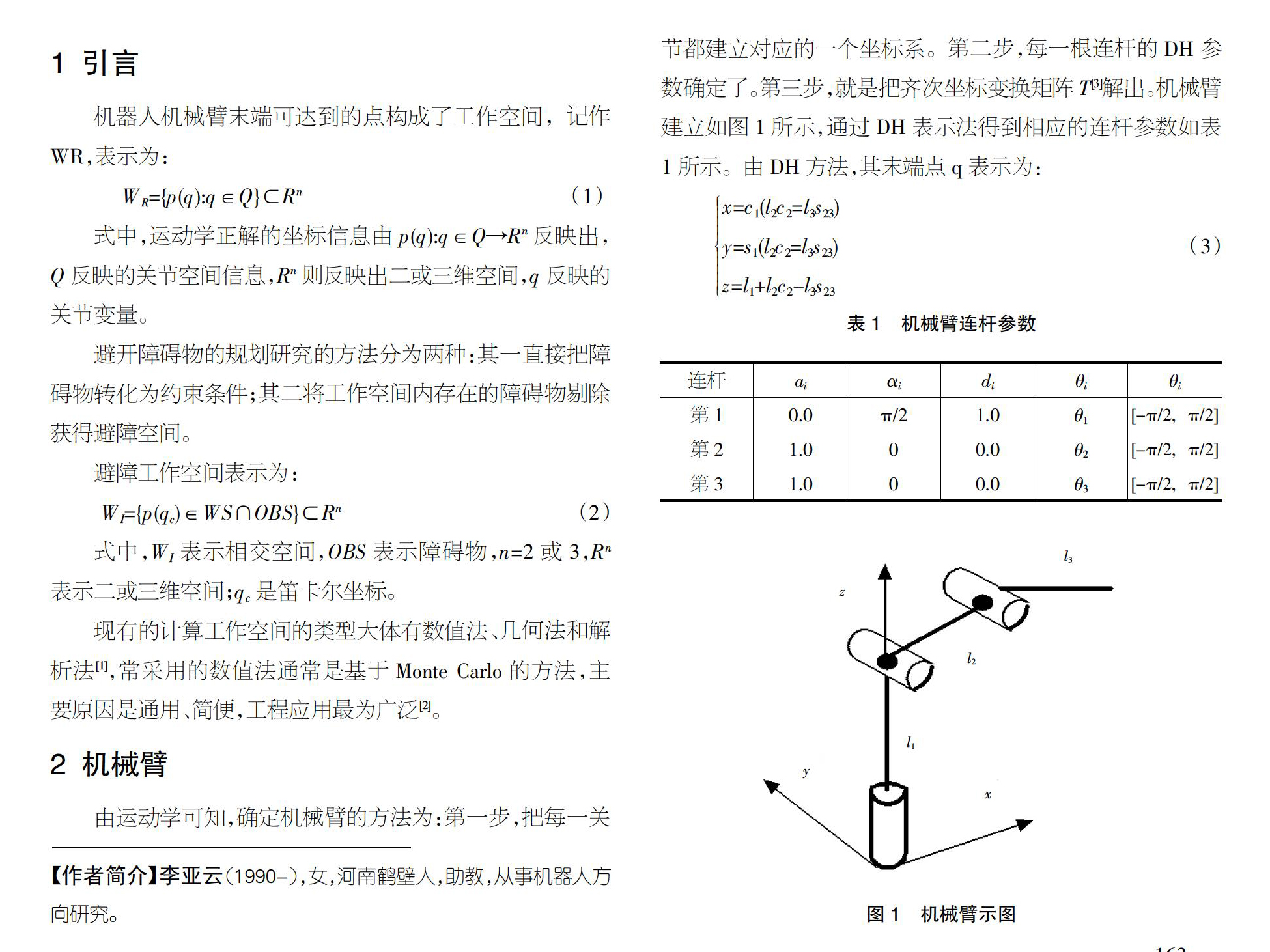
由运动学可知，确定机械臂的方法为：第一步，把每一关节都建立对应的一个坐标系。第二步，每一根连杆的DH参数确定了。第三步，就是把齐次坐标变换矩阵T[3]解出。机械臂建立如图1所示，通过DH表示法得到相应的连杆参数如表1所示。由DH方法，其末端点q表示为：

x=c1（l2c2=l3s23）y=s1（l2c2=l3s23）z=l1+l2c2-l3s23 （3）

3 建立障碍物及工作空间的模型

工作空间模型的生成主要采用Monte Carlo的方法，最终呈现出点云形式，生成模型的方法可以表述[4]为：

①根據求解机器人运动学正解的方法可知，需要利用变换矩阵把所需方程罗列出来，从而获得机械臂末端的具体方位，如（3）式所示。

②确定出关节变量可以旋转的角度，再通过Beta分布的方法获得匹配量的随机值。

③把这些匹配好的随机值运算到（3）式中，工作空间就可以与关节变量匹配为一一对应的情况，进而得到工作空间的云图，如图2所示。

障碍物的圆柱形表面由如下的圆柱函数给出：

x=Rcos？鬃+O3xy=Rsin？鬃+O3yz=u（4）

式中，R是圆柱体的底圆半径，假设为2，而（O3x，O3y）确定成圆心，0≤？鬃≤2π，z=u=7是高度。障碍物的模型就显示出来如图3所示。

4 边界曲线的形成

第一步，按照坐标轴的方向依次连续分割，从而得到对应的一组边界曲线。第二步，按照z轴的方向对每个切片进行边界曲线的提取[5]。第三步，障碍物的点云对应至工作空间的各个切片上，并罗列出整组的边界曲线。

①主要通过Beta的方法来形成工作空间的点云。

②在点云中沿x轴找到最大和最小值，并计算绝对值。

③将区间分为最大和最小值之间的一组等距离的列。

④按照y轴方向找到每列的最大和最小值。

⑤不停重复第2到第4步，但需要交替y轴和x轴。

⑥将找到的边界点依次连接得到闭合边界曲线。

边界多边形可以表示为其不同顶点的（x，y，z）坐标的序列，如下所示：

Wrpolygon?（5）

以上式中的Wr（1， 1）、Wr（1， 2）……Wr（l， w）表示边界点。例如，Wr（1， 2）是片l中的第二点。

立体的障碍物也通过一个式子来获得：

Obpolygon（6）

式中，μ，γ和ω是代表不同切片中的点的值，φ则表示切片的值。工作空间和障碍物的边界曲线如图4所示。

5 OAPW的边界

应用第3节中的做法到不同层的曲线上，即可得出OAPW的轮廓曲线如图5所示。从两个角度绘制三维的相交空间如图6所示。

【参考文献】

【1】黄博，赵建文，姚玉峰，等.面向可避障域的移动操作机运动规划解析方法[J].机械工程学报，2010，46（15）：8-16.

【2】曹毅，李秀娟，宁祎，等.三维机器人工作空间及几何误差分析[J].机械科学与技术，2006，25（12）：1458-1461.

【3】蔡自兴.机器人学[M].北京：清华大学出版社，2009.

【4】陈国汉.蒙特卡洛模拟及其Stata应用实现[M].北京：经济科学出版社，2015.

【5】Cao Y， Lu K， Li X， et al. Accurate Numerical Methods for Computing 2D and 3D Robot Workspace[J].International Journal of Advanced Robotic Systems，2011，8（6）：1-13.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。