《基于KNN与逻辑回归对海难乘客生还率的预测探讨》-管理学论文，管理论文-论文范文参考-科学狗论文网

标题

基于KNN与逻辑回归对海难乘客生还率的预测探讨

范文

陈宇皓

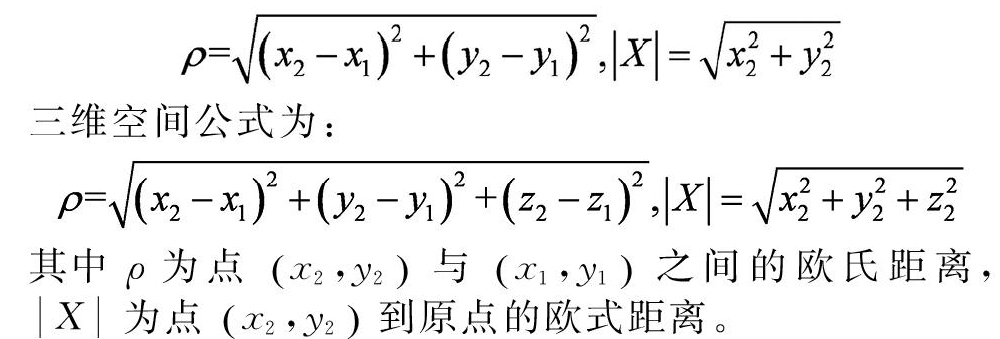
摘要：近日，马航MH370搜救小组正式解散的新闻引起了轩然大波，很多人感叹现在交通救援的发展远远不及交通运输的状况是非常不合理的。在互联网时代下大数据兴起人工智能急速发展的浪潮里，通过对大数据的分析更好的预测不同类型乘客的生还率以协助实施救援，成为非常有效的方法。在对数据处理的各种算法进行学习的时候运用创新思维，以泰坦尼克号的有效数据为例，选择KNN（k-NearestNeighbor）模型和逻辑回归（Logistic Regression）模型，结合数据预处理、可视化分析等方法，对船只失事时乘客的生还率进行预测，同时对比两种模型的优劣，希望对上述方面有实质性的意义。

关键词：KNN;逻辑回归;海上灾难

中图分类号：F24文献标识码：Adoi：10.19311/j.cnki.1672-3198.2019.16.038

1引言

1.1选题背景

海上搜救是指政府、专业部门及志愿者针对海上事故等做出的搜寻、救援等工作，海上搜救仅靠个人的力量是远远不够的，需要全方位的技术支持。提前求援一分钟可能就能够少一分危险，挽救更多人的、奄奄一息的生命。海上搜救不可知因素较多和经验也比较少，因此其难度非常大，政府也一直致力于探索海上搜救如何能及时判断不同类型乘客的存活率，从而第一时间找到最适合救援方案。漫无目的的搜救效率较低，准确的根据乘客特征预测其生还的概率可以提高搜救的效率。

本文以泰坦尼克号乘员的数据为例，结合KNN与逻辑回归两种模型进行探索，希望可以给海上搜救中对遇难者生还概率的判定一定的辅助作用。

1.2研究综述

海上搜救的不可知因素非常多，其难度非常大，并需要较强的技術系统等支持，因此，对海难搜救效率的提升、快速准确的判断乘客生还率非常重要。海难时的天气、地理位置等影响因素都会导致简单的模型无法准确预测，因此需要构建更复杂更严格的模型来进行相关的预测。研究界目前对海上遇难情况中不同类型的乘客的生还率预测有多种方法，如SVM支持向量机模型、逻辑回归模型、卷积神经网络、前馈神经网络等等模型，接下来对本文所用的模型等进行简单的介绍。

1.3本文简介

本文所获取的泰坦尼克号船只相关数据集来自AI领域非常知名的比赛网站Kaggle，通过对数据的可视化分析等找出影响乘客生还的主要因素，对比KNN与逻辑回归两个模型的优势与劣势，结合集成学习的方法进行实验。试验的过程中通过多次观察发现不同的数据预处理对实验结果的影响较大，因此，本文首先针对数据预处理进行了比较详细的介绍。实验过程中，使用交叉验证的方法避免过拟合现象的发生，并通过集成学习的方法进一步提高精度。

2数据预处理

2.1介绍数据与数据预处理

数据（data）是对客观事物的性质、状态及相互关系等进行观察并逻辑归纳的一种物理符号，是一个抽象的概念。数据“属性”是指数据所具有的各种维度的性质，维度过大的数据中常包含一些与预测结果无关的属性，此时便需要通过各种各样的数据降维处理方法进行降维筛选。数据属性也和其他属性一样有其对应的描述单位，我们平时所说的电脑容量，手机内存等等都是如此。

实验中的数据通常来自现实生活，所以得到的数据往往比较杂乱，杂乱的数据并不是信息，只有加工后且有一定意义的数据才可以成为信息。大量的原始数据中有缺失、冗余、错乱等瑕疵数据，数据缺失是指某些重要的数据不完整造成对整体结果的影响，数据冗余是指数据中存在不相关的干扰因素，需要删除。因此，在实验代入算法之前，需要对数据进行一些预处理。

2.2数据预处理的方式

数据预处理形式包括多项，常见的例如：数据清理，数据集成与变换，数据归约，数据离散化及概念分层等，除了这些常规的处理，还有其他可能数据预处理的形式，如数据的压缩存储，包括有损压缩与无损压缩，基于项目的实际意义对数据内容筛选等。本文仅详细介绍数据清理，数据集成与数据变换。

2.2.1数据清理

实验中的数据通常来自现实生活的积累，所以得到的数据往往比较杂乱，无法直接带入算法计算，数据清理便是为了解决这个问题。数据的清理包括识别并消除“噪音”，填充遗漏的值，将数据中的不一致更改为一致等过程，在实验中可根据情况选择其中几个过程。

计算机无法处理为NULL的遗漏值，因此处理遗漏值常采用的措施有两类，忽略和补全。忽略即当此元组缺失属性较多时忽略整个元组，或此属性样本缺失过多时可忽略此属性;补全即通过某种方法将此遗漏补全，常见的方法是根据现有数据的情况用均值等填充某个遗漏值。

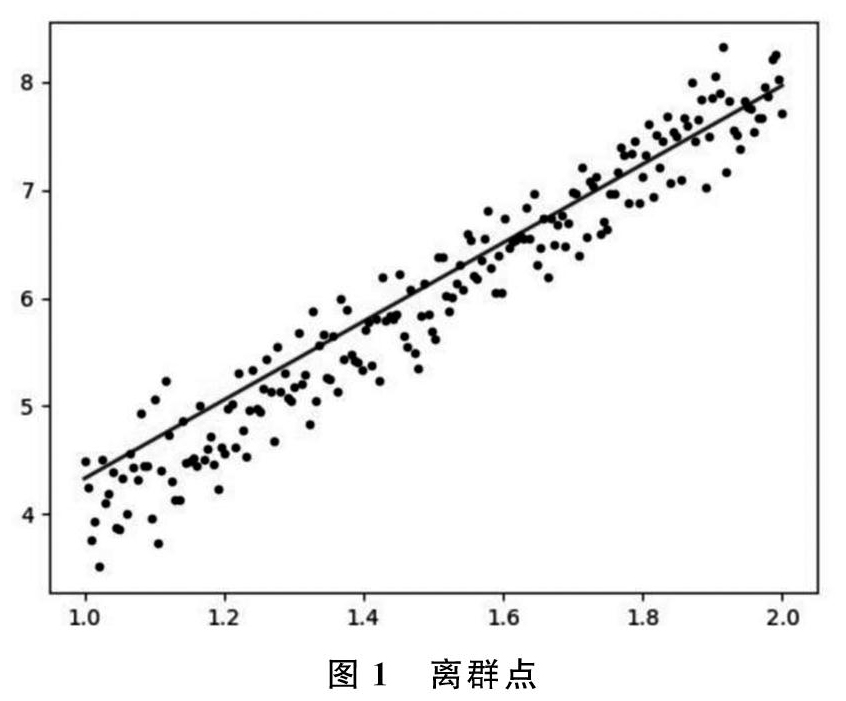
“噪音”的本意是指音量过强而危害人体健康，或引起人烦躁的声音，对于数据而言，“噪音”是指获取数据时出现的随机错误或偏差，例如测量偏差等。去除“噪音”有以下方法：数据分箱是指将数据按照一定规则分布到一些“箱”中，用周围相邻的值来平滑箱中的值。数值聚类是根据规则将近似的值聚集成某种有中心的形状的“类”，落在这个“类”集合之外的值通常可被视为“噪音”。回归分析是现在常用的一种方法，回归分析的原理是拟合出一个可以表达数据之间关系的函数，然后找出离群点。例如最简单的线性回归，即拟合出能表达两个变量之间关系的直线，通过一个变量预测另一个变量（y=kx+b），如图1所示，离直线过远的点即为离群点。

2.2.2数据集成

数据集成是指根据数据相关性将不同数据统一起来。

显然，数据集成中最核心的概念是数据的相关性。数据相关性分为强正（负）相关、弱正（负）相关、非线性相关和不相关。其中，强正相关是指同进退，共同增加或共同减少，强负相关是指你进我退，强正（负）相关均互相变化影响明显，说明A是B的主要影响因素;弱正（负）相关与强正（负）相关类似，但是指变化不明显，即A是B的影响因素，但不是唯一因素;非线性相关是指A是B只有一定的关系，并不是重要的影响因素;不相关顾名思义即两者无关。

2.2.3数据变换

顾名思义数据变换即在不失真的情况下对数据的格式、粒度等进行一定的调整。常见的数据变换有数据规范化，数据泛化，属性构造等。

数据规范化是指为了计算方便、保持不同类型属性权重一致等目的将数据映射到更合理的大小范围内，需保持大小关系不变。常见的规范化有最小-最大规范化等。

数据泛化是将数据集从较低的概念层抽象到较高的概念层的过程。例如，在本项目中，我们需要乘客的年龄，却不需要非常详细的出生年月日，这时可将原有的“出生年月日”属性抽象为“年龄”属性，甚至“年龄层”属性。泛化需要遵循一定的规则，即当属性存在大量不同值，且属性值无法概念分层时，此属性删除，例如“姓名”;当属性存在大量不同值，且属性值可以概念分层，则将属性值概念分层，例如“出生日期”;当属性存在少量不同值时，可保留原属性，例如“船舱登记”属性;当属性不存在不同值时，此属性对预测结果无意义，可删除。

3模型引入

3.1K近邻（KNN）模型

邻近算法，或者说K值最近邻分类算法（KNN，k-Nearest Neighbor）是数据挖掘分类技术中最常见的算法之一。其实质是每个样本都可用它最接近的K邻居来代表，这倒也应了那句古话，“物以类聚、人以群分”，其实在数学上的许多方法就是运用了类似思想。由于KNN方法的核心思想主要依靠需预测值周围有限的邻近的样本，而不是靠判别需预测值类域的方法来确定所属类别，因此，对于类域的重叠较多的样本集来说，KNN方法更为适合。

K值最近邻分类算法（KNN，k-Nearest Neighbor）的核心思想是在特征空间中，如果一个样本在的K个距离最近的样本中的大部分样本属于某个类别，则该样本也属于此类别。根据此思想我们可以知道，“距离”是KNN中最重要的概念。常见的距离计算方式有欧氏距离、曼哈顿距离等，欧氏距离在二维空间中即为高中所学的两点间距离公式，三维空间中加上z轴距离差进行计算。

二维空间公式为：

三维空间公式为：

其中ρ为点x2，y2 与x1，y1 之间的欧氏距离，X 为点x2，y2到原点的欧式距离。

我们要解决的问题中，训练样本包括600个乘客的特征数据。对于测试集的300个数据，计算每一个乘客与训练集中600个乘客的距离远近，从中选出距离最近的K个样本，K个样本中所属类别最多的类别即测试样本的类别。

在实验中，采用sklearn机器学习库中KNN模型算法，尝试了不同的k取值，观察其在该问题上的正确率。测试的结果显示，当k=16时，测试集的正确率最高，在87.8%左右，还存在优化的空间。本实验的训练集仅为600个样本，当上百万训练样本时，KNN算法的局限性就较明显，每预测一个新的样本，都需要计算该样本与上百万样本的距离，运行速度缓慢且效率低下，这时需要选用其他更合适的分类模型。

3.2逻辑回归（Logistic Regression）模型

3.2.1逻辑回归的思想来源

在高中数学中，我们都学过给定两个点的坐标，求得两点之间直线的坐标，“回归分析”则是用直线来拟合多个点的大概走势。在一个坐标系中，分布着许许多多的点，我们用一条直线去尽可能的串联起所有点，再运用此函数图像对需要预测的数据进行预测。

在了解逻辑回归之前，我们先谈谈什么是概率。概率，又称或然率、机率或可能性，是对随机事件发生可能性的一种度量，通常用一个在0到1之间的实数表示事件发生可能性的大小。概率，简而言之，就是描述一件事情发生的可能性。比如随机掷骰子，那么得到任意一个点数的概率是1/6。一件事情的概率，可能性的取值在[0，1]之间。逻辑回归（Logistic Regression）是机器学习中一个经典的分类模型，为什么之前提到概率知识呢？因为逻辑回归模型就是预测一件事情发生的概率可能性。比如预测乘客存活的概率是08，0.7等等。

举个例子，对于一个分类问题，如果想实现我们的分类要求，只需要在特征空间里找到一个“超平面”，即可将两种类别给区分开来。这个超平面也称之为决策边界。比如考试成绩，60分就是一个临界值，可以看作为一个决策边界，所有大于60分的判为及格，所有小于60分的判为不及格。逻辑回归，就是帮助我们找到这样一条“超平面”，能够将不同的类型正确的划分开来。如把存活的乘客和未存活的乘客划分开。

逻辑回归基本原理是采用sigmoid函数作为预测函数，来预测条件概率。在本实验中，sigmoid函数的输出就是乘客存活下来的概率，在训练模型的过程中，通过最小化极大似然代价函数，来不断的提高准确率。

3.2.2逻辑回归的假设函数

假设函数（Hypothesis Representation）的构造方法以多变量线性回归问题为基础，其计算方法为综合考虑多个变量得到其线性组合。而对于二分类问题，假设函数的取值应该满足 0 ≤ h（θ）≤ 1，因此采用非线性函数 Sigmoid 函数（SigmoidFunction）来将任意范围内的值规范化到 [0，1]区间内。逻辑回归方法的假设函如下式：

g（z） = 1/（1+e-z）

我们的模型在训练集上的准确率达到了79.8%，在测试集上达到了81.7%的正确率，取得了良好的性能。逻辑回归的优点是在于简单，训练速度相对于KNN模型快很多。但是其适合用于线性可分的问题当中，而对于一些线性不可分的问题中，采用更复杂的SVM模型可能会取得更好的效果。

3.3集成学习简介

集成学习被认为是各种各样的单一学习的有机统一学习模型，从而获得更准确、稳定和强壮的结果。近年来，各种各样的集成学习模型相继被提出并运用于各种类型的大数据运算中。为了进行更加全面更加有效的预测，我们需要把不同方面的单一学习结合起来，全局进行分析问题。在上文我们已经通过KNN算法与回归模型已经建立起了简单的单一学习。但为进行更加全面更加有效的预测，我们就需要把从不同方面的来的单一学习结合起来，全局进地分析问题。本项目选择Bagging策略来进行准确率的提升。

4结语

本文以泰坦尼克号乘员的数据为例，结合KNN与逻辑回归两种模型进行探索，对比两种模型在该问题上的优缺点。

KNN算法的优点是精度高，对异常值不敏感。但是缺点是对k的取值相对比较敏感，不同的k取值对模型产生的结果可能差异性非常的明显。逻辑回归的优点是在于简单，训练速度相对于KNN模型快很多。但是其一般更适合用于线性可分的问题当中，而对于一些线性不可分的问题中，采用更复杂的非线性模型可能会取得更好的效果。

参考文献

[1]楊丽华，戴齐，郭艳军.KNN文本分类算法研究[J].微计算机信息，2006，22（21）：269-270.

[2]李卓冉.逻辑回归方法原理与应用[J].中国战略新兴产业，2017，（28）：114-115.

[3]范玉妹，郭春静.支持向量机算法的研究及其实现[J].河北工程大学学报（自然科学版），2010，27（04）：106-112.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。