《核心素养下图式理论在高中数学教学中的应用探讨》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

核心素养下图式理论在高中数学教学中的应用探讨

范文

马金凤

【摘要】核心素养是新课改下的教育聚焦，贯串高中数学课标的所有部分，基于核心素养时代的背景，进一步研究数学图式化教学，探讨高中数学如何进行图式教学实践，分析图式理论在数学教学实践中有何作用.

【关键词】核心素养;高中数学;图式理论

图式理论是一种认知心理方面的重要理论，能够将数学的抽象知识转化为具体图式，而图式又是大脑中的一种认知结构.斯根普曾指出：“个别的概念一定要融入与其他概念合成的概念结构中才有效用.”除了所谓最基本的初级概念之外，每一个概念都是由若干较低阶层的概念合并发展得来的，而这个概念其后又与其他概念结合发展出了更高阶的概念.容易看出，图式的建构是抽象化（由较低层次向较高层次的发展可被认为达到了更高的抽象程度）和具体化（除去向着更高抽象程度的发展以外，通过引入新的处于较低层次的概念为较高层次的概念提供具体的“实例”）的一种组合.用图式理论指导数学教学，以引导学生深度学习，激活学生的联想能力，进而培养和发展学生的数学核心素养.

新时代的课程改革要求高中数学课标以“发展学生核心素养”为价值取向及课程主线.借助抽象化、具体化的图式，能够促进学生很好地完成数学知识体系的建构，能够更好地解释学生的学习机制，有助于数学核心素养落实于日常教学.那么，在核心素养时代，高中数学应如何进行图式化教学呢？图式理论在数学教学实践中又有何作用？

1 理清脉络，明确学习方向

图式在指导个体认识新事物时，并不是被动地将其简单搬到头脑中储存，而是按照一定的顺序和逻辑性，将其各个部分形成组块.图式影响着输入信息的选择，并通过一定方式组织信息，将这些信息整合成一个有意义的框架，其目的是促进个体对信息的理解.所以，运用数学图式理清知识脉络，可以提供记忆的支柱，帮助学生理解领会知识.对于数学教学，教师应从分散复杂的知识堆中抓主干，利用图式加工并整理，这样便可给学生的学习提供一个明确的方向.

导数是微积分的核心内容之一，是研究函数的重要工具，衔接着初等数学与高等数学.尽管导数作为选修内容出现在高中教材中，但因其广泛的应用性而成为数学学习的重要内容.因为事物的外部会不断变化，而其内部永恒不变，故认识事物要把握其内在结构，学习繁杂分散的导数亦是如此.在讲解“导数及其应用”时，教师可利用图1的图式来提供知识信息.

图1

由于导数知识繁杂分散，为方便教师的教、学生的学，将导数知识按照内容的内在联系，把相关知识组合成一个学习模块（网络结构）如图1所示，高中导数学习所遵循的主线是：平均变化率→瞬时变化率→导数的概念→研究函数→工具性价值.图1的知识结构图，既表征新的知识，又整合已有的知识，以增强学习的目的性，助力学生认知结构的构建.在理解导数相关知识点的同时，构建以“导数”为主题的图式，强调知识间的内在联系，有利于导数问题的全面把握.通过其中某一个知识点可因知识点间的联系而联想到其他的知识点，即发挥“牵一发而动全身”的效果，这样在面对新的知识时，能够及时提取信息，获得新的方法和策略，特别是在处理综合问题时，能够为其提供多样化的方法和策略.

由此可见，知识结构图转化成学生认知结构的过程就是一种推理过程，也就是说，整体性的思考过程是在发展学生的逻辑推理能力.如果割裂各知识点间的联系，即使能减轻学生的学习压力，也不能减轻处理综合问题的负担，阻碍学生的数学思维，不能帮助学生树立数学应用意识.在教学过程中，教师可以根据实际情况，利用图式理论处理数学知识结构，让学生获得一个明确的学习方向和知识点间的联系.方便提取和再现的知识结构图能够发展学生的“逻辑推理、直观想象”等数学核心素养，符合学生的认知发展规律，促进学生的最佳发展.

2 梳理逻辑，切准问题命脉

图式会影响个体对问题的解決，而问题解决则是个体巩固图式的重要渠道.巧用图式对数学知识进行甄别、组织、整合，构建一个有意义的结构框架，促进学生对新旧知识的衔接、理解、消化与应用.绘制适当的表解图式是迅速表征和解决较为复杂问题的有力手段，往往有助于梳理知识间的逻辑关系或普遍规律，从而缩短审题时间，切准问题命脉，解题时可得心应手.

数列是一种特殊的函数，是揭示自然规律的基本数学模型，其主要内容是数列的概念与表示，教材中通过对生活实际问题的分析，建立等差数列和等比数列两种数学模型.在数列的教学中，教师可以借助表1图式（表解式）引导学生在探索中掌握与等差、等比数列相关的一些基本数量关系.

表1图式的核心思想是类比推理，实际上，等差与等比在运算符号上有密切的联系.教师可以通过表1引导学生观察，启发学生注意观察数列模型的图式（结构）特征，容易发现等差与等比之间的类比遵循上述表格所反映的规律.学习“等差数列和等比数列”的相关知识后，难免会有学生对一些具体知识一头雾水，不能形成完整认知.此时，教师若用图式进行衔接，将等差数列与等比数列进行“平行”学习（每学一个等差数列的性质后，就让学生自主学习、独立探索等比数列与之对应的性质），可形成一个交叉网络，组织学生预测与推理以宏观掌握数学发展的基本线索与数学基础知识之间的关系，进一步对知识再整合、系统化，构建良好的知识网络，完善自我知识体系.

所以，在图式教学中，教师要引导学生：提取信息→加工信息→获取方法→表解式表征，从而分析问题的解决途径.教师引导学生构建适宜的表解式对问题进行表征，能够发挥学生巩固原有知识、激活联想能力的功效;能够培育学生的“逻辑推理、数学建模”等核心素养，培养学生的类比推理思想.

3 构建模型，深化数学思维

皮亚杰认为：“图式描述的是具有一定概括程度的知识而不是定义.”将数学新旧知识间的联系点加工成一个图式，新的知识可转化为已有认知结构中的相关概念，便于更好地掌握新知识.在数学复习课的教学中，教师可以从某一类具有相同属性的数学知识或问题中提炼其本质属性，再拓展到具有这类属性的一切数学知识或问题中，从而以图式的方式形成这类数学知识或问题的普遍概念.

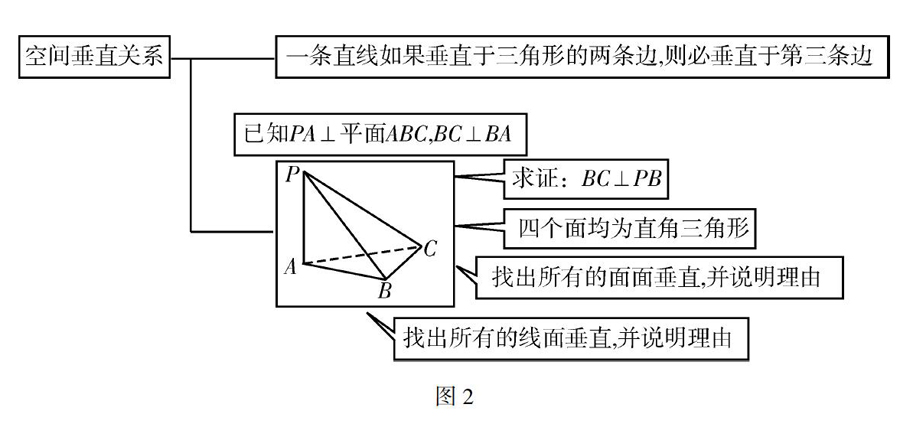
空间垂直关系是高中数学课程中十分重要的内容，要掌握空间垂直的定义及定理和论证相关垂直问题并不那么简单.定义、定理等属于陈述性知识，必须从中整合成适合学生认知规律的相关概念图式，也就是说，图式不是零散的定义或定理，而是一句话和一个典型的样例.对于空间垂直关系，教师可以通过图2的图式进行教学.

图2的教学核心是将空间垂直关系浓缩成一个图式“一句话+几何体”，其中，“一句话”是指一条直线如果垂直于三角形的两条边，则必垂直于第三条边;“几何体”是指四个面均为直角三角形的三棱锥.这个图式比较抽象，要注意的是，在解答垂直关系时，教师既要引导学生养成一种“由因导果”（综合法）的思维习惯：线⊥线→线⊥面→面⊥面;也要培养学生的“执果索因”（分析法）这种逆向思维：面⊥面→线⊥面→线⊥线.而“执果索因”的分析法是非常抽象的.所以，对于一般的学生，最适合的一种程序型图式教学是：将“一句话”与分析法紧密结合，借助图式将空间的垂直关系结构化，然后组成一个模型，这样具有代表性，并且减轻记忆负担.

不难发现，教师引导学生借助已有的知识经验及数学思维构建一种模型记忆的图式，能够培育学生的“直观想象、数学抽象、数学建模”等核心素养，还能够加强学生的文字、符号、图形等语言间的转换能力，从而培养学生的高阶思维.

4 强干弱枝，实现迁移学习

图式以一般期待的形式存在，并通过个体的知觉、记忆和推理过程来预测和控制个人的外部世界[4].在图式的指导下，个体可以利用已有的知识经验处理新的信息，进行由此及彼、举一反三、灵活运用的训练，在已知和未知之间形成迁移，激活个体的创造能力.数学图式中的知识类型包括陈述性知识和程序性知识.数学图式所具备的功能把个体存储的零散知识点贯串起来，使学生能够理清思维，灵活化记忆，对培育学生的创造思维起到启迪作用.

如何让学生进行迁移学习，对所学内容能够触类旁通、学以致用，达到灵活多变的程度？图式能够梳理知识点，建立记忆链条，搭建迁移学习的桥梁和纽带.因此，教师把适宜的图式应用到数学教学中，表达数学知识间的内在联系，使隐性知识显化，引导学生迁移学习.

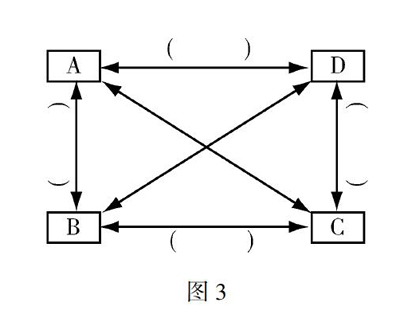
例如，可设计图3的图式让学生思考，如果图3表示的是“原命题、否命题、逆命题、逆否命题”四种命题之间的关系，字母A，B，C，D分别代表哪种命题？括号中应填什么内容？这四种命题的真假性之间有什么关系？同时，若用小写字母p，q表示命题的条件与结论，则四种命题如何表示？

教师可以依照图3设计图式，重组知识结构或留下空白，检查学生的学习效果，帮助学生记忆.数学图式中的“留白”是一种艺术表达方法，让学生有丰富的想象空间，故而可将其作为一种教与学的策略，教师以此法激发学生独立思考问题的欲望，培养学生学习的能动性、协作性和创造性，激励学生学会学习，这样将会提高学生的自学能力和反思性思维，还能发展学生的数学核心素养.

综上，数学知识图式的表达方式不是一成不变、封闭的，而是不断演化、开放的，它能使学生巩固知识，灵活记忆，加深理解，激发创造性.在图式系统中，图式因知识的延伸学习而深化思维，迁移受图式驱动，智慧随迁移闪烁，创新被智慧点亮，从而改变着学生的认知方式，丰富着学生的认知结构，使得问题显化而更易于处理.

在数学教学中，尝试从知识的脉絡、性质、概念、迁移等方面去探索图式理论的应用，在一定程度上扩展知识的广度，追求技能的深度，加强知识的同化.因此，数学图式教学并非“填鸭式”教学，而是抓住知识的内涵与外延，进行有的放矢的数学教学，让学生逐渐认识到数学的核心知识，内化知识结构体系，从而培养学生的数学核心素养.

【参考文献】

[1]吴健.学生对周期函数概念的理解[D].上海：华东师范大学，2007：4-5[2007-10-01].

[2]陈素琼.图式理论在高中化学教学中的应用研究[D].福州：福建师范大学，2016.

[3]张文婷.概念图在高中生物教学中的应用[D].扬州：扬州大学，2015.

[4]王星星.高中生化学图形认知能力的探查[D].扬州：扬州大学，2012.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。