《转化思想在小学数学“图形与几何”教学实践中的应用》-教育论文，课程教育论文-论文范文参考-科学狗论文网

标题

转化思想在小学数学“图形与几何”教学实践中的应用

范文

代春红

【摘要】数学思想是对数学对象本质的认识，是基本观点和根本想法，对于学生的学习而言有着十分重要的作用，其中转化思想为数学思想中最基本的思想之一，可以帮助学生将知识化繁为简、化曲为直，有效降低學生的学习难度，提高教学质量，意义重大。对此，本文针对小学数学教学中转化思想的运用进行了深入的分析，以“图形与几何”教学为例，以期能够为相关读者提供积极的参考。

【关键词】小学数学? 图形与几何? 转化思想? 应用

【中图分类号】G623.5 ? 【文献标识码】A 【文章编号】2095-3089（2020）12-0154-02

引言

转化思想是小学数学教材中众多数学思想方法之一，是非常普遍的一种常用数学思想方法。而小学是学生数学学习的重要启蒙阶段，引导学生去理解并掌握数学转化思想十分关键，是未知领域通过数学元素之间的因果联系向已知领域延伸的重要手段，能够找出数学因素之间的本质联系，进而解决实际的问题，有利于学生高效率的学习，提高学生的思维品质。总体而言，转换思想的具备是小学生攻克各种复杂问题的利剑，例如数形结合思想就是充分体现了数和形之间的转化。因此，在小学数学“图形与几何”教学中，教师要重视转化思想的有效利用，以培养学生数学思想，提高其数学素养和能力。

1.深入挖掘教材文本，培养学生的转化意识

文本教材是知识的载体，是向学生传递知识的重要途径，其中蕴含着非常多的能够解决问题的数学思想方法，但是教材的呈现是静态的例子，并没有十分明确的指出或者揭示其中知识结构所包含的转化思想。因此，小学数学教师在实际的教学实践中，要深入研究数学教材内容，掌握其结构体系的地位作用，把握其中转化思想的本质，提炼转化思想，进而去培养学生的数学思想。从教学目标设定上教师就要重视数学转化思想的培养。在小学数学“图形与几何”教学中就涵盖着非常明显的转化思想，例如三角形的三个内角转化为平角，平面图形面积公式的推导过程用到转化思想，三角形与多边形的内角和学习也蕴藏着转化思想。另外，立体图形体积之间的相互转化等。所以，在实际的教学过程中，教师要深入挖掘教材知识内容的转化思想，精心设计教学过程。当然在设计的过程中，教师还需要掌握学生已有的知识储备，以此为基础科学开展教学活动。

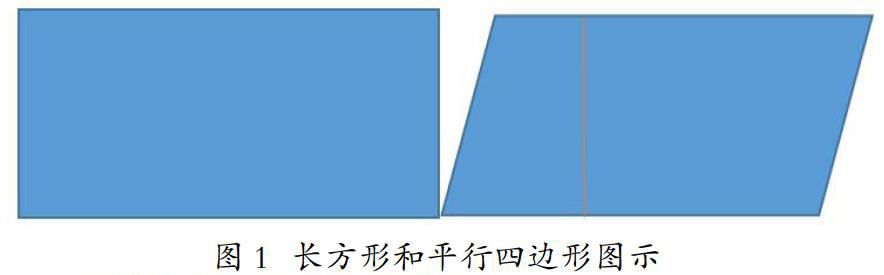
例如：在教学平行四边形的面积计算知识内容时，到这一阶段的学生都已经具备了基本的长方形、正方形以及三角形的特征和面积公式，也认识什么是平行四边形。接着为其提供一个长方形和平行四边形（如图1），拥有相同的长和高，这时教师就可以以此为基础，引导学生去计算，明确认知冲突，接着让学生仔细观察，以探索交流的方式去进行思想、观点的碰撞，进而找到正确的推导方法，渗透图形转化思想，充分发挥学生的空间意识，培养学生转化意识。

2.精选教学方法，应用转化思想

在小学数学的“图形与几何”教学中，其教学内容大多是比较抽象的，对于以形象思维为主的小学生而言是比较困难的，因此，教师要选择适合学生的较直观的方式进行知识的传授，渗透转化思想。如借助直观的教具或者多媒体等，将抽象的立体图形直观化、动态化、形象化，这样一来学生能够更容易的去了解和掌握“图形与几何”的知识内容。

3.通过实践操作，应用转化思想

随着素质教育的深化，新课程标准针对小学数学教学提出了动手操作的要求，而动手操作是学生学习数学知识和参与数学活动的重要方法，所以，在“图形与几何”教学过程中，教师就可以利用动手操作调动学生积极性的同时，有意识的引导学生应用转化思想，如拼一拼、剪一剪、量一量、测一测等方式，促使学生能够更深刻、形象的去理解所学知识，领悟转化思想，例如：在教学三角形面积计算时，就可以组织学生进行拼一拼、剪一剪的活动，引导学生将两个完全相同的三角形拼成一个长方形或者平行四边形，或者将一个长方形沿对角线剪成两个完全相同的三角形等，从而推导出三角形的面积计算公式。

结语

总之，数学转化思想是数学思想的重要基础性组成，对于学生的学习、思维的转化有着十分重要的作用，教师教学必须重视转化思想的有效应用，培养学生转化意识，提高学生转化能力，以实现学生的全面发展，提高其数学素养。

参考文献：

[1]贺慧贤.转化思想在小学数学教学中的渗透[J].课程教育研究，2018（29）.

[2]林丽琴.转化思想在小学数学教学中的运用——以“图形与几何”教学为例[J].福建教育学院学报，2019（02）.

[3]王首创.浅谈小学数学教学中如何培养学生的转化思想[J].数学大世界（教学导向），2012（12）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。