《中职学生学习三角函数的意义》-教育论文，职业教育论文-论文范文参考-科学狗论文网

标题

中职学生学习三角函数的意义

范文

[摘? ? ? ? ? ?要]? 中职三角函数相关知识不仅广泛应用于力学、电学、电磁学、工程学、天文学、医学等专业领域，而且对中职学生未来的生活以及创新能力的培养也具有非常重要的指导意义。

[关? ? 键? ?词]? 三角函数;广泛应用;能力

[中图分类号]? G712? ? ? ? ? ? [文献标志码]? A ? ? ? ? ? ? ? ? [文章编号]? 2096-0603（2019）24-0038-02

数学是中等职业教育课程中的基础学科，在教学过程中得不到应有的重视，特别是三角函数相关知识的教学，由于知识点多且抽象，解题时灵活性、综合性也较强，学生时常表现出难以驾驭的倾向。因此，在许多中职学校数学教学过程中呈现出放弃现象，但它广泛应用于力学、电学、电磁学、工程学、天文学、医学等专业领域，对我们中职学生数学思维的形成以及创新能力的培养都具有重要的指导意义。

一、三角函数是许多中职学生学习专业知识的基础

《中等职业学校数学教学大纲》中指出中职数学课程教学目标：在九年义务教育基础上，使学生进一步学习并掌握职业岗位和生活中所必要的数学基础知识。

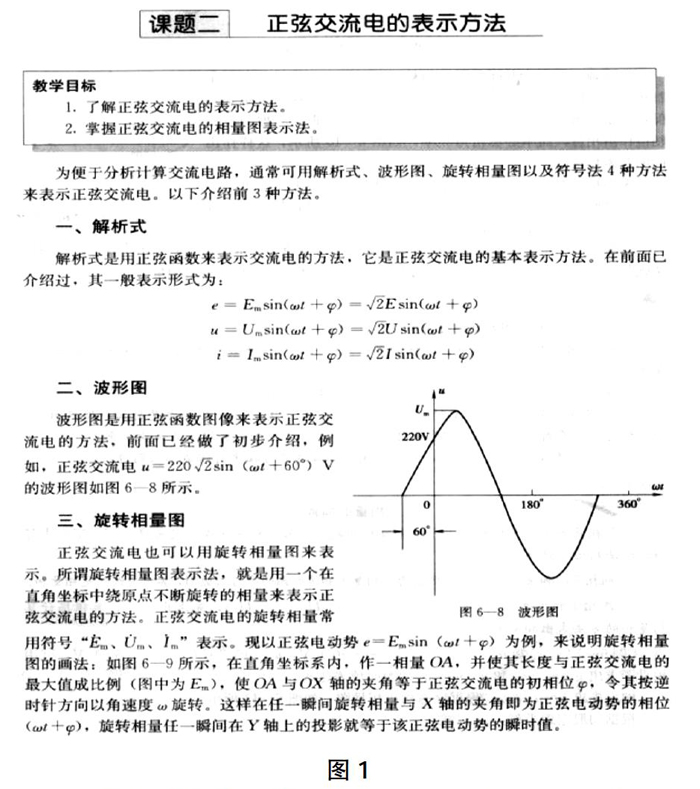
现在让我们走进中职《电工电子技术基础》教材第139页（图1）。

再者，中职机械专业学的《电工基础》（第三版）第22～23页上的一道例题（图2）。

同样，在我们的《数控加工工艺与编程》第34～35页也可以看到神奇的三角函数踪影，这里由于篇幅限制，不再用图片展示。

总之，三角函数及其相关知识的触角伸向了职业教育的诸多领域，它是我们学习专业知识的基础。

二、三角函数对学生解决实际生活中的问题也有非常重要的促进作用

三角函数由于精确地描述了三角形中边和角的关系，广泛存在于我们的生活中。如在测量上，利用它可以测得山高、树高，河对岸两点间的距离;在航海行程上，利用它能解决暗礁、台风等问题;在建造上，抓住它能确定光线与房屋结构是否合理等。

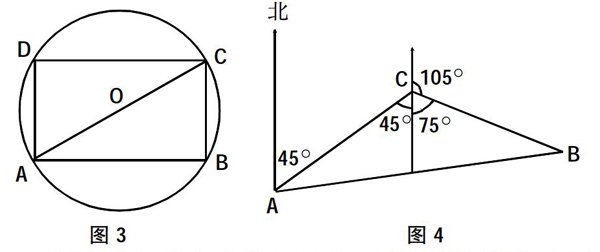
例1：（如图3）把一段半径为R的圆木，锯成横截面为矩形的木料，怎样锯才能使横截面积最大？

例2：（图4）一渔船在航行中不幸遇到飓风，发出求救信号，假设我海军舰艇在A处获悉，立即测出该渔船在方位角为45°，距离A为10海里的C处，并测得渔轮正沿方位角为105°的方向，以9海里/时的速度向小岛B靠拢.我海军舰艇立即以21海里/时的速度去营救，求舰艇应按什么方向前进才能靠近渔船？

国务院总理李克强2014年2月在部署加快发展现代职业教育的会议中提出要打通从中职、专科、本科到研究生的上升通道，积极推进学历证书和职业资格证书“双证书”制度。三角函数对中职学生的学历学习起着至关重要的作用。

三、中职三角函数对学生“学历”的影响

（一）全国成人高考试卷中的三角函数

全国成人高等学校招生统一考试（简称成考），它是为我国各类成人高等学校选拔合格新生以进入更高层次学历教育的入学考试。它属于国民教育，它是国家高等教育重要组成部分，它与普通高等教育是一种相互依存、相互完善的关系。三角函数在成考中的地位不容小觑（如表）。

近几年全国成考（高起点理工农医类）试卷中三角知识考查情况

从这几年的试卷中可以看出：三角函数对中职学生成考成绩的影响不容忽视，由前几年的二十几分，逐渐攀升到三十几分。

（二）三角函数在高等数学中也有举足轻重的作用

在复数的运算中由于引入了三角函数的相关知识，从而使复数之间的乘法、乘方运算都大大地简化了。如两个复数之间的乘法用公式表示为Z1·Z2…Zn=…=r1（cosθ1+isinθ1）·r2（cosθ2+isinθ2）…rn（cosθn+isinθn）=r1r2…rn[cos（θ1+θ2+…+θn）…isin（θ1+θ2+…+θn）]，即积的模等于两个复数模的积，积的辐角等于两个复数的辐角之和;以此类推，一个复数的n（n∈N）次幂可表示为Zn=[r（cosθ+isinθ）]n=rn（cosnθ+isinnθ），即乘方后的模为原来复数模的次幂，辐角为原来复数辐角的倍，这就是著名的棣莫佛定理;同样，在微积分中由于引入了三角函数（这里角的单位是）得出了：（sinx）'=cosx;（cosx）'=-sinx。另外，曲线的极坐标、参数方程等知识点均与三角函数有着千丝万缕的联系。

四、三角函数的教学有利于促进学生良好思维品质的形成

良好的思维品质包括思之快、思之活、思之深、思之新。新课改推行之后，我们改变了传统的教学理念，注重学生发散思维和创新能力的培养。一题多解、一题多变是培养学生创新能力的有效途径，它不但可以激发学生的好奇心和求知欲，而且能够增強学生的应变能力，让学生在解题过程中打破思维定式的影响，多方位、多角度观察、分析、解决问题，提高主体的思维发散能力。在三角恒等证明题中有这样一道题：证明。此道题可以使用七种方法来证明，也就是说它可以使用七种思维方式来解决;同样，正弦定理的证明也存在六种方法等，通过这些问题的解决，不仅能巩固学生所学知识，而且能促进学生的思维触角伸向不同的方向，不同的层次，有利于学生思维灵活性和广阔性的形成以及创新能力的培养。

另外，三角函数知识中还蕴含着大量的数学思想，如对应与映射思想、分类讨论思想、变换与转化思想、数形结合思想、化归思想、函数与方程等。

总之，在中职阶段开展三角函数的教学可以让学生的数学思维能力得到极大的培养和提升。

参考文献：

[1]于建华.电工电子技术基础[M].2版.北京：人民邮电出版社，2011.

[2]人力资源和社会保障部教材办公室组织编写.机械基础[M].北京：中国劳动社会保障出版社，2011.

[3]钟玉泉.复变函数论[M].3版.北京：高等教育出版社，2009.

[4]李小红.中职三角函数教学现状调查与策略研究[D].西宁：青海师范大学，2019.

◎编辑武生智

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。