网站首页  词典首页

请输入您要查询的论文：

　

标题 巧构全等三角形解几何问题
范文 李小兰




[摘? ?要]对于初中几何问题，若给定的题设条件及图形并不具有明显的全等条件时，可通过添加辅助线，构造全等三角形去解决.巧构全等三角形，可借助全等三角形的有关性质，使已知与未知发生联系，促进已知向未知转化，从而顺利解决问题.
[关键词]全等三角形;几何问题;辅助线
[中图分类号]? ? G633.6? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058（2019）08-0027-02
全等三角形是初中几何的重要内容之一，也是解决几何证明题必不可少的工具.然而在许多情况下，给定的题设条件及图形并不具有明显的全等条件，这就需要我们开阔视野，打开思路，多方位地寻找添加辅助线的方法，构造出全等三角形，借助全等三角形的有关性质，使已知与未知发生联系，促进已知向未知转化，从而使问题得以顺利解决.
[案例1]《利用角平分线解决相关几何题》的复习课
本节课分两部分内容，一是先让学生探究利用角平分线构建全等三角形的方法;二是解决问题.
1.引导学生建构模型
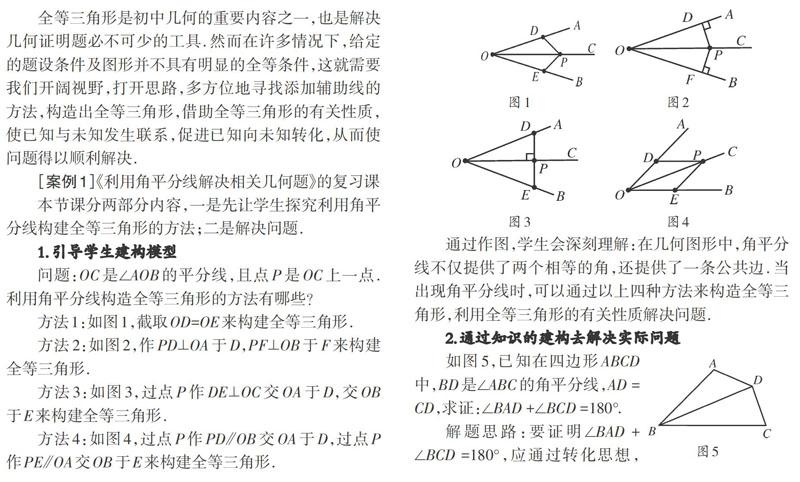
问题：OC是∠AOB的平分线，且点P是OC上一点.利用角平分线构造全等三角形的方法有哪些？
方法1：如图1，截取OD=OE来构建全等三角形.
方法2：如图2，作PD⊥OA于D，PF⊥OB于F来构建全等三角形.
方法3：如图3，过点P作DE⊥OC交OA于D，交OB于E来构建全等三角形.
方法4：如图4，过点P作PD[?]OB交OA于D，过点P作PE[?]OA交OB于E来构建全等三角形.
通过作图，学生会深刻理解：在几何图形中，角平分线不仅提供了两个相等的角，还提供了一条公共边.当出现角平分线时，可以通过以上四种方法来构造全等三角形，利用全等三角形的有关性质解决问题.
2.通过知识的建构去解决实际问题
如图5，已知在四边形ABCD中，BD是∠ABC的角平分线，AD = CD，求证：∠BAD +∠BCD =180°.
解题思路：要证明∠BAD +∠BCD =180°，应通过转化思想，让学生联想到平角，再通过等量代换，利用全等三角形构建一个平角.
方法1：如图6，在BC上截取了BE=AB.
∵BD是∠ABC的角平分线，
∴∠1=∠2，
在△ABD和△BDE中，
BE=AB，∠1=∠2，BD=BD.
∴△ABD≌△BDE，
∴AD=DE，∠A=∠3，
∵AD=CD，
∴DE=CD，
∴∠4=∠C，
∴∠3+∠C=∠3+∠4=180°.
方法2：如图7，过点D作DM⊥BC于M，作DN⊥BA的延长线于N，构建△NBD≌△BDM和△AND≌△DCM.（证明略）
方法3：如图8，延长CD交BA的延长线于点F，构建△FBD≌△BDC.（证明略）
学生在理解了角平分线的建模后，引发思考并找到了本题添加辅助线的方法（如图7的三种方法），从而顺利构建全等三角形，使问题得到解决.学生在学习中通过模型的思想来解决数学问题，思维得到发展，提升了思维品质.
[案例2]如图9，在Rt△ABC中，AB=AC，∠BAC=90°，O为BC的中点.如果点M、N分别在线段AB、AC上移动，且AN=BM，判断三角形OMN的形状.
解题思路：这是一个特殊的三角形，考虑到等腰三角形的三线合一定理，所以要判断三角形OMN的形状，先要考虑证明OM=ON，通过转化思想，证三角形全等，但题目没有出现全等三角形，所以难点在于构建全等三角形.
方法1：△OMN为等腰直角三角形.理由如下：
连接OA，如图10，AC=AB，∠BAC=90°，
∴OA=OB，OA平分∠BAC，∠B=45°，
∴∠NAO=45°，
∴∠NAO=∠B，
在△NAO和△MBO 中，
∴△NAO≌△MBO，
∴ON=OM，∠AON=∠BOM，
∵AC=AB，O是BC的中点，
∴AO⊥BC，
即∠BOM+∠AOM=90°，
∴∠AON+∠AOM=90°，
即∠NOM=90°，
∴△OMN是等腰直角三角形.
方法2：如图11，连接OA，过点O作OE⊥AC于E，作OF⊥BA于F，构建△OMF≌△OEN.（证明略）
解题分析：利用了“三线合一”定理和角平分线的定理添加了辅助线，从而得到OE=OF，再利用余角的性质得到∠MOF=∠NOE，得到了三角形全等，进一步解决了问题.
方法3：如图12，连接OA，过点M作MH⊥BC于H，作NG⊥BC于G，构造△OMH≌△OGN.（证明略）
解题分析：利用了“三线合一”定理和构造直角三角形添加了辅助线，从而得到OE=OF，再利用余角的性质得到∠MOF=∠NOE，得到了三角形全等，进一步解决了问题.
评析：本題是特殊三角形的综合性考题，考查等腰三角形的“三线合一”定理、等腰三角形的判定与性质、全等三角形的判定与性质等.本题属于中等难度题，但图形比较常见，由证线段相等转化为证三角形全等.在证明三角形全等时，利用两个角互为余角进一步证明两个角相等也是常用的方法.本题通过三种方法添加辅助线来构造全等三角形，从而让问题得以解决.
（责任编辑 黄桂坚）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/11 0:51:22