《精心设计问题导学　促进数学深度学习》-教育论文，中学教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

精心设计问题导学　促进数学深度学习

范文

汤忠芳

摘要

复习是一个完善和深化所学知识的关键环节，是对所学内容的有效整合。数学教师通过问题引领，以一种清晰而又灵动的教学设计思路，展开数学复习课的教学，既能帮助学生巩固、消化基础知识，又能促使知识内化，助推学生深度学习，为学生的可持续发展奠基。

关键词

复习课初中数学问题导学深度学习

数学复习课是围绕一个核心知识点，通过问题设计，将相近或关联的知识进行类比和整合、拓展与延伸，以再现、整理、归纳等方式，将教学内容一步步地逐层深入，使之条理化、系统化，以便学生加深对知识的理解和应用。问题的选择和优化，是提升复习课教学效率的根本所在。为避免一些简单知识的机械重复，问题的选择应具有聚合性、深刻性和全面性;问题的优化应注重知识和能力的提升。教师应精心设计问题导学，关注师生间的交流生成，通过师生促进和生生促进，促使学生深度学习，从根本上提高数学复习课的实效，提升学生的数学学习力。

一、课堂教学的基石——“数学模型”的选择与构建

“数学模型”就是把数学问题抽丝剥茧，形成的一种能够推而广之的结构。数学建模就像搭建一座高楼，从学生的感受上讲是一个心理过程，从形式上讲是一个创造性的思维活动;数学建模不是做题，更不是题目的简单堆积，而应该是“一种活动”的升华。

在“用一元二次方程解决问题”的教学中，有这么一道经典例题（增长率问题）：某钢铁厂去年1月某种钢的产量为5000吨，3月上升到7200吨，这两个月平均每个月钢产量增长的百分率是多少？这类问题可以总结为：若原来的量为a，平均增长率是x，增长后的量为b，则第1次增长后的量是a（1+x）=b1，第2次增长后的量是a

（1+x）2=b2......第n次增长后的量是a（1+x）n=b。增长率问题的模型就是a（1±x）n=b（其中a是原来的量，b是现在的量，增长取+，降低取-，n表示次数）。结合复习课教学实际，尤其是解决几何问题时，教师可引导学生适时采用以下方式：

（1）有则组之——根据题目条件特征，看题中信息是否有关联，若有，把它们组合联系构成完整数学模型;（2）缺则补之——若题目中没有现有模型，可以添补所缺元素构造完整数学模型（辅助线的构造）;（3）无则变之——若题中信息孤立，看不出与之相关的模型，则观察题中是否存在某种变换关系，通过内在联系构建数学模型，帮助学生实现知识的“再发现”“再探索”“再生成”和“再应用”。

二、教学深度的体现——习题选择的变式与拓展

复习课的深度体现在习题的选择上。习题既要发散变化，拓展联系;又要能深入本质，整合归一。复习课例题的选择，应是最有代表性和最能说明问题的典型习题。教师要善于从例题这个单一知识点向多个知识点发散，发挥例题以点代面的作用，有意识地在例题基础上进行系列的变式，通过挖掘问题的内涵与外延，达到在变化中寻找规律，在变式中内化知识的目的，实现复习的知识从量到质的转变。

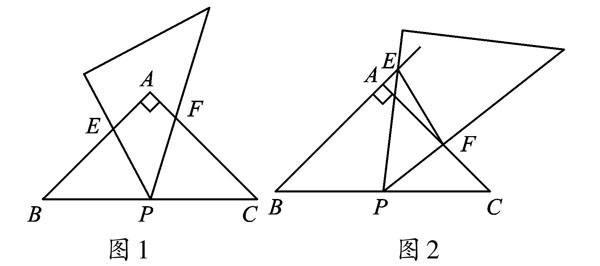
如在复习“相似三角形”时，可选例题如下：等腰直角三角形ABC中，∠A=90°，P为BC的中点，小明拿着含45°角的透明三角板，使45°角的顶点落在点P上，且绕P旋转。（1）如图1，当三角板的两边分别与AB、AC交于E、F点时，试说明△BPE∽△CFP;（2）将三角板绕点P旋转到图2，∠P的两边分别交BA的延长线和边AC于点E、F。探究1，△BPE与△CFP还相似吗？探究2，连接EF，△BPE与△EFP是否相似？请说明理由。

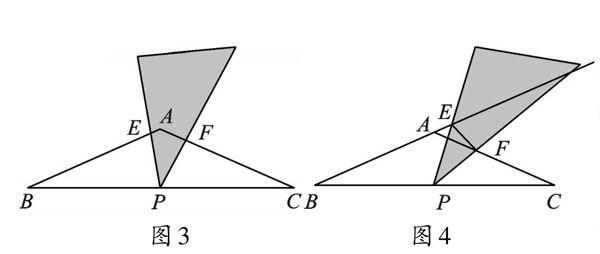
变式：等腰△ABC中，AB=AC，∠BAC=120°，P为BC的中点，小明拿着含30°角的透明三角板，使30°角的顶点落在点P上，且绕P旋转。（1）如图3，当三角板的两边分别交AB、AC于点E、F时，试说明△BPE∽△CFP;（2）操作，将三角板绕点P旋转到图4情形时，三角板的两边分别交BA的延长线、边AC于点E、F。探究1，连接EF，△BPE与△PFE是否相似？请说明理由;探究2，设EF=m，△EPF的面积为S，试用含m的代数式表示S。

本例题通过对基本图形的变换，加强学生读图能力的培养，让学生深化对此类问题的理解。教师在复习课选择习题时，要结合学生实际，丰富复习课习题训练的形式，通过开放性的问题，选择能够适应和提升不同阶段学生层次的数学练习，进行分类讨论，发展思维能力，实现学生能力的整体提升。

三、知识生成的启迪——“问题串”的设计与优化

复习课的作用是将知识向纵深推进，通过问题串”将各个知识点借助题目进行有机融合，从而将知识形成系统，织成一张知识结构网，遵循“逐步推进、螺旋上升、不断深化”的认知规律，让学生能站在更高的层次去重新领悟所学的知识。

以“一次函数”的基本知识复习课为例。已知函数y=（3-k）x-2k+9。问题1：若已知函数是一次函数，求k的取值范围。问题2：若已知函数的图像经过原点，求k的取值范围。问题3：若已知函數的图像与y轴的交点在x轴上方，求k的取值范围。问题4：k为何值时，已知函数y随x的增大而减小或已知函数图像经过一、二、四象限。问题5：直线y1=（3-k）x-2k+9与直线y2=3x+5交于P（-1，a），求k的值;x为何值时，y1

复习课应是以问题为核心，以效率为目的的课堂。“适合每一个”是我们课堂追求的出发点;“发展每一个”是我们课堂生成的落脚点。如何使学生在“重基础、会思考、强能力”的课堂教学中游刃有余，是数学复习课课堂优化的最终目标。因此，每一位数学教师，都要结合日常的思考和平时的积累，以题带点，以境串型，以变促能;通过有效引导，科学合理地展开教学，逐步培养学生自主学习和综合探究能力，让数学课堂焕发新的光彩。

（作者单位：江苏省常州市金坛区河头中学）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。