《数学线上教学如何提高质效》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

数学线上教学如何提高质效

范文

马燕

摘要：线上教学时，可通过线上前测，了解学生的学情，明确教学重难点。《一次函数的图像与性质》一课线上教学，有效突破教学重难点的方法有：设置探究学习单，勾连学生已有经验;运用信息技术手段，使操作过程更直观;借助在线测评系统，及时评价反馈。

关键词：线上教学探究学习单信息技术在线测评系统《一次函数的图像与性质》

疫情防控期间，中小学校积极开展线上教学工作。这是应对疫情、保障“停课不停学”的应急之举，也是“互联网+教育”的有益应用和实践探索。线上教学时，针对学情，一节课的教学重难点如何确定？采用哪些教学手段，才能有效突破教学重难点，做到“披沙拣金”，更好地提高线上教学的质效？这些都需要细加揣摩。带着相关思考，笔者开启了《一次函数的图像与性质》的线上教学之旅。

一、开展线上前测，明确教学重难点

“一次函数的图像与性质”知识既是初中数学教学的重点，也是难点。学生在此之前几乎没有研究函数图像问题的知识和经验，加之函数图像比较抽象，这就导致这部分知识学习的困难直线上升。而函数知识贯穿整个初中数学学习，学生对于一次函数的图像与性质的掌握程度、研究函数图像问题积累的经验和方法将直接影响到后续其他函数的学习。

为了更好地了解学生对函数的已有经验以及本节课中可能存在的认知障碍，笔者在课前设计了一组试题进行了前测。前测结果既有意料之中的，也有意料之外的。比如，大部分学生能够在简单的实际问题中正确选择出与之相对应的函数图像，但对于一次函数的图像是什么、怎么画知之甚少;对于求出一个一次函数与坐标轴交点坐标的问题，正确率比较低;几乎没有运用数形结合思想研究函数图像的经验。

针对这样的前测结果，笔者将本节课的教学重难点明确为：经历描点法画函数图像的过程，知道一次函数的图像是一条直线（理解画函数图像的方法是关键，渗透数形结合的思想也不可或缺）;会求函数与坐标轴的交点坐标，会选取两个适当的点画一次函数的图像（基本技能的提升与画图方法的优化）;在列表、画图的过程中体会数形结合与化归的思想。

二、实施线上教学，突破教学重难点

为了更好地突破教学重难点，笔者结合前测对学生学情的分析和线上教学的特点，主要运用以下三种方法实施了《一次函数的图像与性质》一课的线上教学。

（一）设置探究学习单，勾连学生已有经验

为了激发学生的已有经验，笔者设置了如下探究学习单：

1.再次重温我们熟悉的气温变化图（如图1），你能获得哪些信息？气温变化图是用图像来表示气温T是时间t的函数，请问函数是否都可以用图像来表示？那么一次函数可以用图像来表示吗？

2.气温变化图是由一系列的点构成的，能具体指出一些点吗？可以用表格呈现出来吗？用图像法表示函数的关键是什么？请用正比例函数y=2x来说明，并尝试在平面直角坐标系中画出该函数图像。

3.一次函数图像为什么是一条直线？画一次函数图像需要注意什么？

笔者让学生以小组为单位，在独立思考的基础上开展线上的小组讨论。小组的思考可通过语音或在评论区留言的方式和大家分享，以促进全班对于探究式问题的深度思考。

第1题，通过气温变化图，引导学生回顾函数的定义，建立函数与图像之间的对应关系，激发学生探求函数图像的意识。第2题，让学生用表格的形式呈现气温变化图中部分点的坐标，旨在激发学生的已有经验，用列表的方式找到具体函数中一组组对应的x、y的值以及在坐标系中找到一组组以x、y的值为横、纵坐标的点，从而帮助学生建立起图像上的点与满足函数关系式的实数对之间的对应关系。第3题，在学生充分经历画的过程之后，引导学生思考，形成数学化的认识。因为是自主探究，学生的回答显然有些不尽如人意，表现为对函数的理解不到位、数学语言表述不够规范等。但是，对实际问题的探究，能够帮助学生理解研究函数图像的必要性，体会列表描点画图方法生成的自然性。

（二）运用信息技术手段，使操作过程更直观

本节课教学，引导学生经历画函数图像的过程非常重要，教师需要进行示范演示。在线下教学中，通常可以通过板书呈现，那么在线上教学中该怎么办呢？我们可以通过“QQ直播”中的“屏幕分享”功能，采用笔记本电脑+平板（手写笔）+几何画板（画函数图像的软件）+希沃授课助手（同屏显示软件）的组合，动态呈现教师画函数图像的全过程。

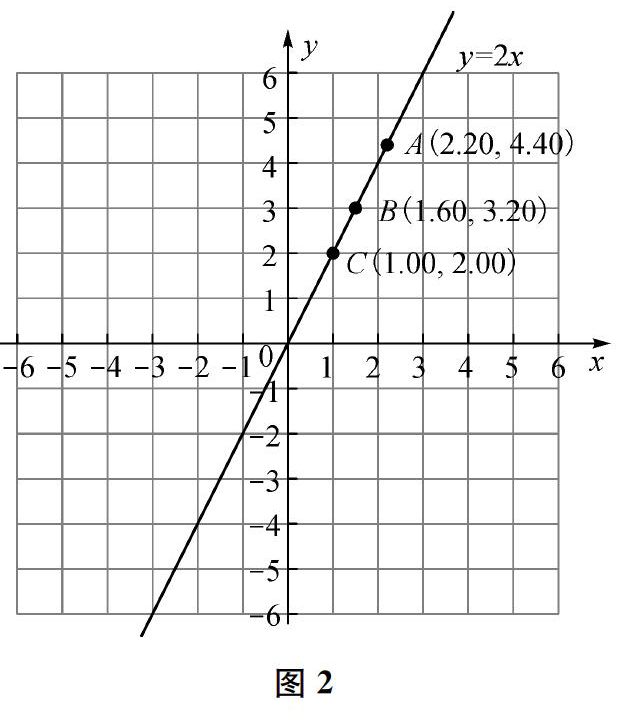
首先，在几何画板软件中，取若干组满足一次函数y=2x自变量和因变量的取值，作为坐标点，直观呈现点逐渐增多直至形成一条“直线”的过程（如图2）;然后，反过来，在直线图像上取一些点，令学生将其坐标值代入函数关系式y=2x，验证是否满足。

直观的示范操作，可以帮助学生从纯粹性和完备性的角度理解一次函数图像是一条直线，为后续取两点画图像的方法做好准备，也可以进一步帮助学生从变量取值以及点的坐标之间的对应关系体会数形结合的思想，这对学生后续研究其他类型的函数图像有积极的作用。

（三）借助在線测评系统，及时评价反馈

线下的随堂检验，教师一般只能选取部分学生的作答情况进行展示，这容易造成教师对学生本节课学习掌握情况的不到位。而线上教学平台一般都配有在线测评系统，学生当堂完成教师布置的检测题的，系统会自动批改，生成全班学生的答题情况。这样，教师能快速、全面地了解学生的知识掌握情况，第一时间做出评价和反馈。同时，这也有利于教师对学生进行个别化的辅导和教学总结。

本节课，笔者利用在线测评系统布置了如下随堂检测题：

1.在平面直角坐标系中，一次函数y=x-1的图像是（）

A. B.

C. D.

2.一次函数y=kx+b（k≠0）在平面直角坐标系内的图像如图3所示，则k和b的取值范围是（）

A.k>0，b>0

B.k<0，b>0

C.k>0，b<0

D.k<0，b<0

3.如果一次函数y=kx-3的图像经过点（2，-6），那么k=。

4.一次函数y=2x+6的图像与x轴的交点坐标为，与y轴的交点坐标为。

5.一次函数y=2x+b的图像经过第一、三、四象限，则b0。

6.在同一直角坐标系中画出下列函数的图像：

（1）y=2x;（2）y=2x-3。

学生作答后，通过在线测评数据分析发现，学生对于本节课内容的掌握情况良好，关于计算函数与坐标轴的交点坐标的技能以及数形结合思想的运用能力均有明显提升，主要表现为第1、3、4、6题的得分率均超过80%。但借助图像理解函数的性质还不到位，主要表现为第2题的得分仅为39.1%，第5题的正确率为52.2%。其中，第2题的正确选项为B，而选择A和D的人数偏多。究其原因，学生缺乏解决这个问题的方法，没有从函数的增减性角度思考k的正负性，也没有正确理解函数图像与k、b取值的关系。因此本节课在方法层面的教学上还存在一定缺失，需要在后续教学中加以改进。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。