《信息技术，让数学教学可视化》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

信息技术，让数学教学可视化

范文

张志勇

摘要：推进现代教育技术与数学教学的深度融合，用信息技术让数学教学可视化是一个重要的思路。具体地，可以从抽象到直观、从演绎到归纳，让教学内容可视化;在创设问题情境、开展实验探究以及拓展构造应用时，让新知教学可视化;通过绘制思维导图、搭建感知平台，让主题教学可视化。

关键词：数学教学信息技术可视化

现代科学技术，特别是计算机科学、人工智能的迅速发展，正在深刻影响着我们的课堂，为其提供了无限的可能。如何推进现代教育技术与数学教学的深度融合？用信息技术让数学教学可视化，是一个重要的思路。这样，不仅能够充分发挥信息技术快捷、精准的优势，而且可以让数学变得“平易近人”，让数学教学变得生机勃勃。具体地，可以从以下几个方面入手：

一、让教学内容可视化

通过信息技术，将抽象的数学学习对象（概念原理、结构关系、思想方法等）用直观、具体的形式生动、清楚地呈现出来，化数学“冰冷的美丽”为“火热的思考”。

（一）从抽象到直观

抽象是数学最基本的思维方式，然而抽象的知识需要变成直观的形式，才能够更好地被学生感知和理解。此外，数学抽象源于数学直观，因此，应用信息技术将抽象的数学“还原”成直观的数学，可以让学生在抽象活动中，积累抽象经验、学会抽象方法。

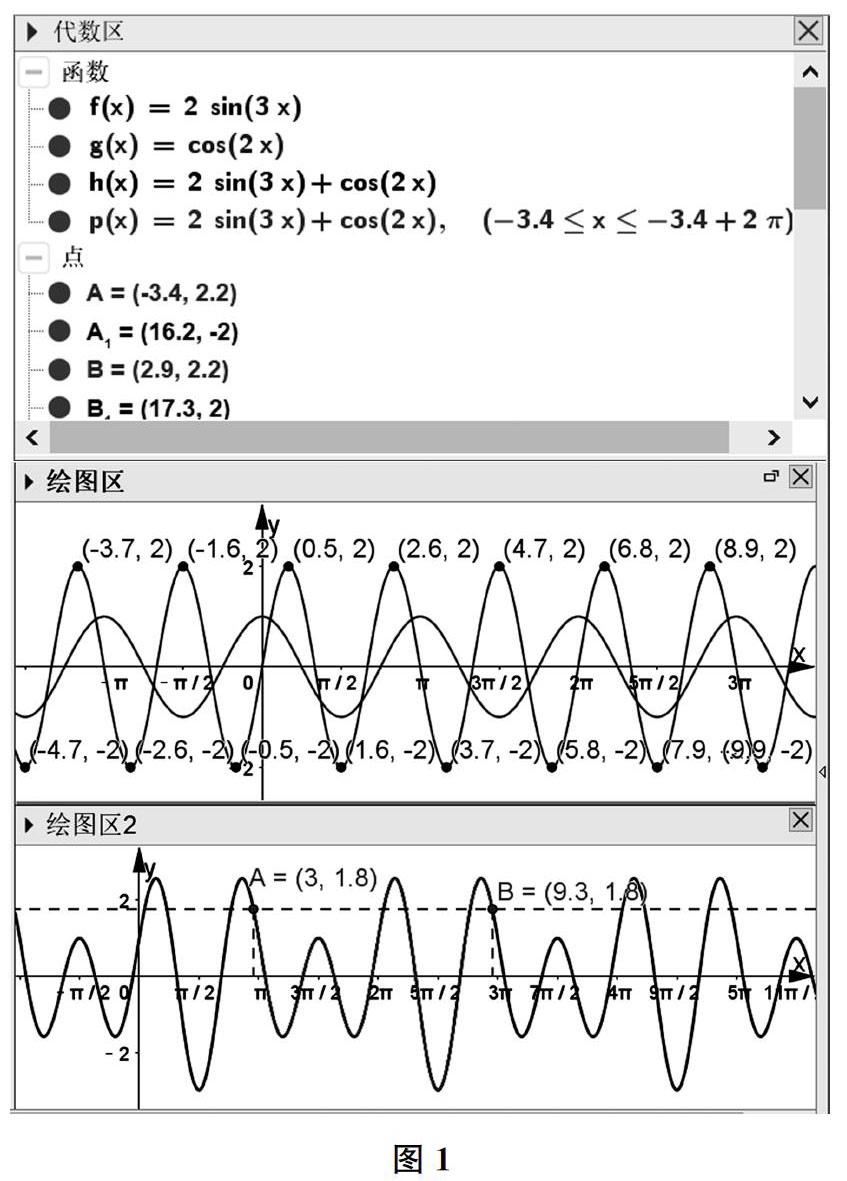
例如，高中数学教材一般是从“周而复始”的生活现象抽象出函数周期性这一数学概念的，但是，要用数学语言“存在非零实数T，对于任意的x，都有f（x+T）=f（x）”来描述，学生就勉为其难了。如果利用现代数学软件提供丰富的函数图像（如下页图1，不限于基本三角函数的图像），让学生经历从“形”到“数”的抽象过程，学生对函数周期性概念的理解就能全面而深刻了。

再如，教学“矩阵与变换”时，有必要通过现代数学软件中一些图形的构造，来建立矩阵（代数范畴）与变换（几何内容）的纽带。

（二）从演绎到归纳

数学讲究演绎推理，但是不能没有归纳猜想。事实上，当我们有了某种数学想法时，最简单、直接的做法就是寻找一些具体的例子来证实。而有了较为充分的具体例子，就可以从中概括出一般性的结论，并且证明方法往往也已经蕴含在具体的例子中了。于是，化演绎为归纳，也成为让数学（广义的）可视化的一种可行路径。特别地，现代数学软件大多内嵌符号代数系统（CAS），于是，有关公式、法则的学习都可以通过归纳的方式进行。

以两角和的正弦公式为例，可以通过CAS运算直接给出几个运算结果（如图2），让学生观察运算结果，归纳发现其中的数学规律。有了具体事例的支持和发现过程的展开，运算规则更易于“深入人心”。

事实上，现代数学软件中，代数区、绘图区、3D绘图区、运算区、工作表等多模块的关联互动，可以完成几何作图、代数运算和数据处理等数学工作，做到很多过去课堂中完全做不到的事情，

实现“向技术学习数学”。可以说，“懂得现代数学教育技术，她就會给你独到的眼光，让你洞悉数学世界”。

二、让新知教学可视化

（一）创设可视化问题情境

问题情境是新知探究的起点和载体，可以激发和启动学生的主动思维，不仅能帮助学生“入课”（通过探究获得所学知识），而且能帮助学生“出课”（从应用的角度认识所学知识的价值）。创设问题情境时，可以充分利用信息技术，进行可视化表征，从而通过“图示”的方式，突破“意会”与“言传”之间的障碍。

a2+b2≥2ab，右图表明a+b2≥ab（更多的信息有待学习基本不等式后进一步挖掘）。由此，可以很好地引发学生的学习兴趣。

（二）开展可视化实验探究

数学实验是一种以实际操作、观察为特征，强调动手实践的数学探究、发现、理解活动。它符合学生的认知规律，能让学生经历数学知识建构从猜想到验证的全过程，而不是简单地应用数学知识解决问题。数学实验具有直观化、具体化的特征。数学实验教学可以利用实物模型展开，更可以利用信息技术高效展开。

例如，学习“圆锥曲线的概念”时，学生很难将平面的椭圆、双曲线、抛物线与立体的圆锥联系起来;即便有足够的空间想象力，也很难由截线定义过渡到轨迹定义。于是，可以利用现代数学软件再现Dandelin双球实验，让学生在如图4（其中的“代数区”内容被略去）所示的平台中“做”实验：

改变α、β的值（α、β分别表示母线、截面与z轴的夹角），观察截线的形状，生成圆锥曲线的截线定义（通常情况下，β>α时，截线为椭圆;β<α时，截线为双曲线;β=α时，截线为抛物线）;引进Dandelin双球，在不同视角下观察双球与圆锥及截面的相对位置关系，从而凸显球与圆锥的切线、球与截面的切点（即圆锥曲线的焦点）的关键作用;结合平面视图，考察截线上任意一点到焦点距离与到切线距离的关系，从而生成圆锥曲线的轨迹定义。

事实上，在操作过程中，也就得到了相应的几何证明（以椭圆为例）：构造截线上任意一点M和圆锥过点M的母线m，设m和双球与圆锥的切线分别交于点P、Q。由球外一点引球的切线长相等，可知MF1=MQ，MF2=MP，于是MF1+MF2=MQ+MP=PQ（PQ为定值，与点M的位置无关）。

（三）拓展可视化构造应用

问题驱动获得知识后，还要应用知识（解决问题）。除了创设问题情境、开展实验探究时，可以利用信息技术开展可视化教学之外，应用知识时，也可以充分利用信息技术进行可视化表征——特别是构造新的满足概念定义或结论条件的例子时。

例如，在高中数学教学中，函数周期性一般是借助三角函数来研究的，但其并非三角函数所独有的。于是，应用周期性“构造”新函数（如下页图5所示），不仅必要，而且可能。

三、让主题教学可视化

数学教学不能满足于数学知识的获得与应用，更要着力于数学思维的发展和素养的培育。如果学生学到的数学知识只是一个个的孤立的点的话，那么，这样的内容很难稳固地保存、清晰地检索和准确地提取。事实上，数学思维和素养的成分难以在单个的知识点上表现出来，它往往隐藏在知识结构（体系）中。因此，数学教学要从聚焦细小的知识点或课时中跳出来，关注更大的主

题或单元。开展主题（单元）教学，要从广泛的角度、用联系的观点看待和分析问题，引导学生整体地思考和认识，连点成线、结线成面，建立知识联系，形成知识结构。而这一过程也离不开信息技术可视化效果的辅助。

（一）建立知识结构

辅助主题（单元）教学的一种重要方式是，利用相关软件引导学生绘制思维导图，实现思维过程和结果的可视化，突破思维的局限，从而厘清数学知识发展的内在逻辑，构建一个个或大或小的知识结构。

例如，教学“三角恒等变换”后，教师可以引导学生绘制如图6所示的知识框图。

再如，教学“三角函数”前，教师可以引导学生梳理指数函数、对数函数和幂函数的学习经验，形成如图7所示的函数学习基本范式，从而明确三角函数的研究应从角的概念推广开始（解决定义域问题），并得出推广中需要满足新概念兼容旧概念、运算性质基本不变等基本要求。

（二）搭建感知平台

辅助主题（单元）教学的另一种重要方式是，利用现代数学软件，搭建感知平台，促进学生的理性思考。

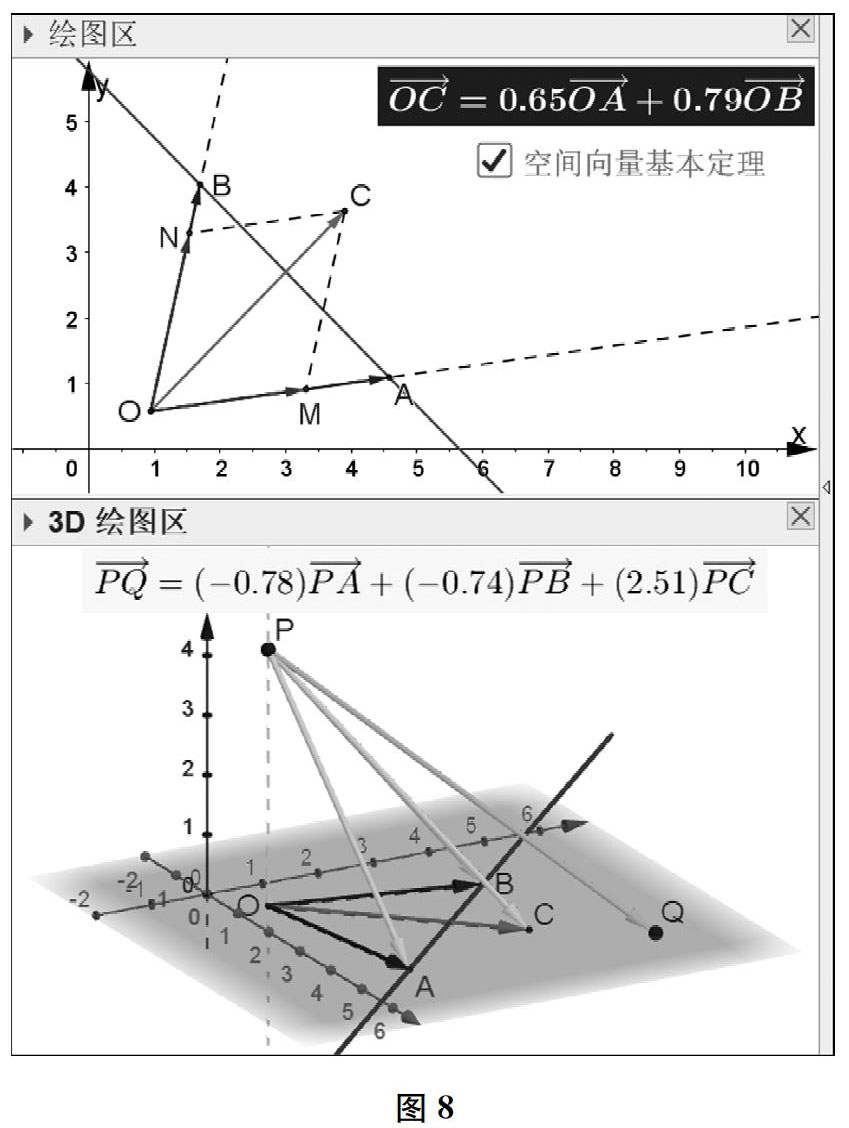
在这一过程中，借助如图8所示的软件平台进行实验感知，在获得丰富的感性认识的基础上进行推演论证，从而保证层次清晰、意义明了的认知结构的真正建立。

*本文系江苏省中小学教学研究第十三期课题“可视化视角下高中数学阅读与表达教学的实践研究”（编号：2019JK13L106）的阶段性研究成果。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。