《二次函数在生活中的建模应用》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

二次函数在生活中的建模应用

范文

沙之超

【摘要】数学建模是培养学生创新意识和应用能力的重要载体，本文通过对二次函数知识点的研究，采用相应的教学方法，体现二次函数在生活中的建模应用，由简入难地驱动学生完成相应的目标任务，由此激发学生的学习兴趣，培养学生的实践和创新能力.

【关键词】二次函数，建模，任务驱动，应用教学

函数是重要的数学思想，在实际生活中充当了数学建模的重要工具，因此，二次函数的课程中，有大部分内容都拥有很强的理论性，具有一定的抽象性，故而在学生普遍对二次函数在生活中应用兴趣不浓，觉得乏味枯燥，这就需要在二次函數在生活中的应用中构建数学模型，将建模思想引入实例中，发现问题并能解决问题，这样不仅能提升二次函数的趣味性，更能提高学生分析问题和解决问题的能力.数学建模思想在二次函数中的应用，对教学效果有很大帮助，与此同时利用任务驱动的教学方法，可以大大增加学生学习二次函数的理论知识和实践生活的应用的学习兴趣，让学生参与数学建模解决实际问题的整个过程，体验二次函数的应用价值.

一、任务设计

某设计公司在一次商品推介会上为了抓住商机，专门设计了一款产品，其成本为20元/件，请为该公司考虑如何定价、定量，才能使得该公司的利润最大化.

提出问题：每件产品有固定的成本，那么该产品的利润和什么挂钩？

将学生进行分组，小组讨论，归纳并总结讨论的结果：与生产的单价、产品的质量、销售量等等相关.通过学生的参与，教师进行相应的总结，假定排除一些不必要的因素，只考虑与生产和销售相关的因素，那么不难得出利润=销售总价-成本总价，销售总价=销售单价×销售量，成本总价=成本单价×销售量.根据这些变量之间的关联，教师设计两个任务，学生进行探讨，任务一是探究销售单价和销售量之间的关系，任务二是探究如何定价定量才能使得销售利润最大化.

二、实施任务

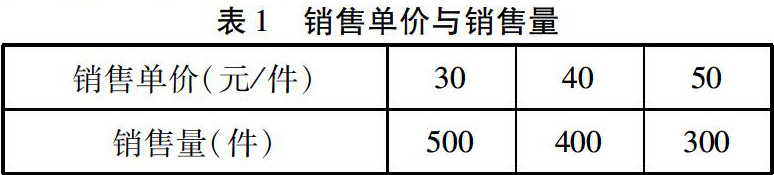
任务一：通过实践调查，同时考虑到市场中该件商品的销售单价会有一定的涨幅，与此同时销售量也会下降，故得到如下数据（该数据已知）.

模型构建：需要学生进行分组讨论，从三组数据中，学生能否得出两个量之间的关系，在探讨的同时，教师也需要一定程度地参与.

在教师的启发下，学生可以得出函数关系，设销售单价为x，销售量为y，将对应形成的三个点（30，500），（40，400），（50，300）代入y=kx+b，得k=-10，b=800，因此，y=-10x+800（20≤x≤80）.

任务二：根据以上的销售单价与销售量之间的关系，当销售单价为多少时，才能获得最大的利润，此时最大利润是多少，产量是多少？

学生进行分组讨论，自主构建模型.设利润为z，得z=（x-20）y=（x-20）（-10x-800）=-10x2+1 000x-16 000（20≤x≤80），化简得z=-10（x-50）2+9 000（20≤x≤80），求解得出当x=50时，zmax=9 000，y=-10×50+800=300，因20≤x≤80，x=50符合该区间，因此，当销售定价为50元/件时，能够获得最大的利润为9 000元，工厂生产此件商品的产量为300件.

三、教学反思

（一）任务分解，合二为一

对二次函数在实际生活中的应用而言，可以通过任务驱动教学法来进行对实际问题的剖析和解决.在遇到实际问题时对总任务进行相应的任务分解.任务一的设计具有挑战性，根据三组离散的数据得出销售单价与销售量之间的关系，学生无从下手，但在教师的点拨启发下，通过函数作图得出二者的关系.任务二的实施由学生自主完成，教师只参与任务结果的评价，该任务的完成鼓舞了学生的学习兴趣，完成这两个任务之后就对其总任务进行总结归纳得出总结论.

（二）由简入难，难易适中

在二次函数的模型的分析和建构中，巩固二次函数的主要知识点，掌握数学建模的一般步骤，培养学生的建模能力和实践应用能力.本着这一目标，根据初中生数学基础薄弱、学习兴趣不浓、应用能力弱的实情，教师创设了设计公司销售产品的情境，由此引出总任务.围绕利润，学生展开讨论，切合生活实际，列举了许多与利润有关的因素，课堂气氛活跃.教师又把总任务细化成两个小任务.任务一：根据提供的数据得出销售单价与销售量之间的关系.从最简单的一次函数入手，遵循由简入难的原则，让学生在第一个任务中碰到的问题较少，解决方法也具有一定的开放性，采用散点图进行图像拟合，得出一次函数模型.任务二由学生自主完成，通过构建二次函数模型可得以解决，让学生感受数学建模的一般步骤，同时对二次函数知识点进行一定程度的理解和加深.

（三）自主建模，教师引导

在二次函数建模过程中，教师要设计恰当的问题，唤起学生思维，参与积极和创造.通过对问题的提出，创设了一个宽松、融洽的课堂环境，学生也能够积极参与讨论，无拘无束地进行交流探索活动.教师要为学生搭建建模活动必要的认知平台，在他们遇到困惑时，给予适当的引导和启发，但并不包办代替，在学生讨论无果，探究遇到障碍时，适时给予探究的线索，重燃学生探究的信心.

四、结论

由于初中学生对实际问题的解决意识较为缺乏，故而需要在日常的数学教学过程中对学生的数学应用能力进行一定程度的培养，通过对二次函数在实际生活中建模的应用，利用任务驱动教学方法将建模思想融入一个一个的任务中，这样既能激发学生学习的兴趣和积极性，更能让学生学会自主解决数学问题.

【参考文献】

[1]曹经富.例谈二次函数的建模与应用[J].初中生，2009（21）：38-41.

[2]基于数学建模的高中函数教学设计研究[D].重庆：重庆师范大学，2017.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。