《小学数学教材的合理改造》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

小学数学教材的合理改造

范文

刘兆伟

随着课程改革的不断推进，不少教師已经不再拘泥于教教材，而是尝试创造性地使用教材。但不少教师在改造教材时，由于缺乏对教材的深入解读，以致出现目标定位不当、逻辑顺序混乱、价值认识偏差等问题。笔者认为，在改造教材时，应深入解读教材，充分把握数学学科本质、学生认知及心理发展规律，以保证其合理性与有效性。下面结合苏教版数学教材中的一些例子，谈谈笔者的一些认识。

一、在知识脱节处衔接

数学知识具有完整的结构和严密的体系，学生对数学知识的认识是一个螺旋上升的过程。教材在编排时，理应考虑数学知识之间的联系，努力实现前后知识之间的无缝对接。但由于受学生的认知规律及年龄特点所限，教材在编写时无法将连续性的数学知识集中在一起，只能把它们分散到各册教材中，所以有时会出现前后知识不能顺利衔接的现象，这时就需要教师帮助学生在合适的时间补上相应的内容，以保证数学知识的整体性和连续性。

如苏教版《数学》五年级下册“异分母分数加、减法”一课中，教材给出的计算方法是先通分，化成同分母分数后再计算。但学生在三年级上册“分数的初步认识”单元中学习同分母分数加、减法时，主要目的是为了帮助学生理解分数的意义，所以并没有归纳出一般的计算方法。因此，在学习异分母分数加、减法之前，须要通过复习回顾提炼出同分母分数加、减法的计算方法，以便学生能够顺利实现算法的转化和迁移。

二、在经验断层处弥补

学生的学习总是从其已有的知识经验和思维经验出发，在新旧知识间的冲突中，运用旧有的经验解决新的问题，在此过程中产生新的经验。但在一些内容的学习中，学生的已有经验不足以解决新的问题，此时，新旧经验之间是存在断层的。在教学中，我们须要架设新旧经验之间的桥梁，使新的经验从旧有经验中产生，以补上经验的断层。

如苏教版《数学》五年级上册“三角形的面积”一课中，探寻三角形面积公式最需要的经验是倍拼法，而学生的已有经验是通过剪拼法将平行四边形转化成面积与其相等的长方形。显然，学生根据已有的经验是很难想到倍拼法的，他们的经验是存在断层的。教材的处理方法是将三角形放在平行四边形中求面积，直接将倍拼法呈现在学生面前。这样设计虽能让学生快速得到结论，但不利于学生思维能力和自主探究能力的发展，难以帮助其积累思维活动经验。笔者在教学这一内容时，先给学生提供多个不同类型的三角形（其中有等腰三角形），学生在尝试把三角形转化成已学过的图形时发现：只有等腰三角形可以运用以前的剪拼法转化成长方形，从而求出面积。进而由等腰三角形的剪拼经验联想到任意两个完全一样的直角三角形可以拼成一个长方形，从而使学生获得倍拼法的经验，并用此经验探索任意三角形的面积计算公式。

三、在认知易混处厘清

在小学数学中，有些学习内容涉及多种内涵，多种内涵之间既有区别，又有联系。在初学时，如果将同一内容的多种内涵放在一起学习，容易使学生产生认知障碍，理不清它们之间的区别与联系，这种对同一内容多种内涵之间关系的模糊认识会给后续学习带来障碍。因此，在认识具有多种内涵的教学内容时，我们可以先学习其中的一个，等对这一个已经有了清晰的、深刻的认识时，再学习下一个，最后再把它们合在一起认识，这样效果会好。

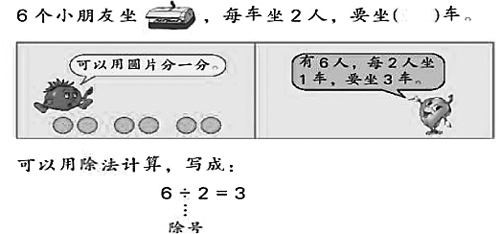
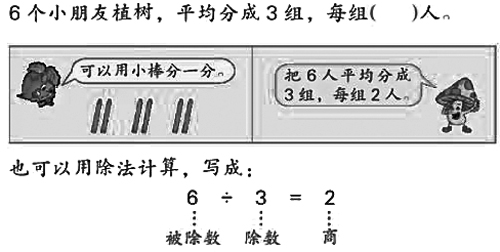
如苏教版《数学》二年级上册“认识除法”一课，本课是学生第一次接触除法，而除法有两种类型：包含除与等分除（图1、图2）。教材将这两种类型的除法安排在同一课时中教学，这势必导致学生难以区分除法的这两种模型，进而给学生理解算理带来了障碍。因此，必须帮助学生对这两种模型建立起清晰的认识。笔者将这一单元分成两部分来教学，先让学生在丰富的平均分物的基础上认识等分除，当学生对等分除有了深刻认识后再进行包含除的操作与认识，实践证明，这样改造效果更好。

四、在需要欠缺处激发

教材中的学习内容都是经过精心选择的，或与生活有关，或与将来的进一步学习有关，其安排有一定的逻辑性和层次性。其中有些内容在学生目前的生活中用不到，但对未来的学习与生活又是十分重要的。学生当下难以体会到其价值，所以难以产生学习的需要。他们缺乏学习动机，学习行为将会是被动、低效的。对这样的学习内容，我们理应创设合理的学习路径，激发学生的学习需要，使学习行为由被动接受式转变为主动建构式。

如苏教版《数学》三年级下册“数据的收集与整理（二）”一课，教材中先让学生在各小组内收集数据，再把各个小组的数据汇总成全班的数据。在教学中，有学生提出这样的想法：“解决例题中的问题只需要按月份举手，再数一数就行了，不需要这么复杂的方法”。可见，学习这种收集整理数据的方法时，学生是没有学习需要的，甚至是排斥的。怎样才能引起学生的学习需要呢？笔者在出示例题后，先让学生说说可以用什么方法收集数据，学生想到了举手数一数、一一询问、先分小组收集再汇总等方法，再问学生解决例题中的问题用什么方法最好，学生一致认为举手数一数的方法最好，其他方法比较麻烦。最后笔者追问：“为什么教材中选用了先分小组收集再汇总的方法呢？”学生深入思考后，认识到这种方法的价值：在收集较大范围的数据时，比如调查全校所有学生的出生月份时，难以使用举手数一数的方法，而先分组收集再汇总就比较方便了。在学生认识到这种方法的价值后，学习的需要被激发了，学习的热情提高了。

五、在理性薄弱处明理

小学数学教材中有很多探寻规律的学习内容，在这些内容的教学中探寻规律的成因既是对事物由表及里的认识过程，又是提高学生探索能力、培养理性思维的过程。但考虑到学生的思维能力及年龄特点，教材在这些内容的安排中降低了对学生理性思维的要求，这有合理的一面，但有时不利于学生理性思维的培养。在这些内容的教学中，我们可以用学生能够理解的方式，让学生用自己的语言对规律的成因给出适当说明，让学生逐步养成言之有理、言之有据的思维习惯，并形成探寻现象成因的意识。

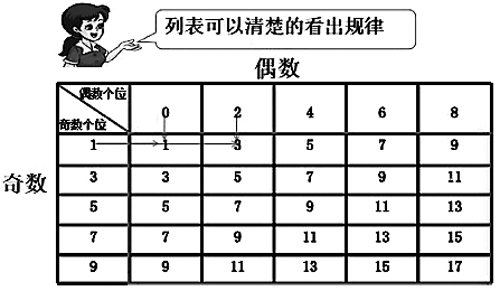
如苏教版《数学》五年级下册“和的奇偶性”一课，教材先让学生自己任选两个不为0的自然数相加，看看和是奇数还是偶数，再通过对多个算式的观察得出猜想：偶数+偶数=偶数，奇数+奇数=偶数，奇数+偶数=奇数，最后举例验证猜想。我们知道，对有无数个研究对象的命题，通过举例验证方式并不能一定得到确定的结论。为了让学生感悟结论的确定性，笔者在学生举例验证后，进一步引领学生进行理性探究。因为一个数的奇偶性只和其个位上的数有关，所以研究和的奇偶性只需要看两个加数及和的个位上的数就行了。在这样认识的基础上引领学生列表（图3），因为此表中列举了奇数加偶数的和的个位上数的所有情况，所以学生能根据其能得到确定的结论，接着让学生用同样的方法验证另外两个猜想。这样的设计将教材中的举例验证升华为完全归纳验证，在此过程中，学生的理性思维得到了培养。

总之，在改造教材时，我们要结合理论与实际，深入思考并探寻更为合理的学习路径，并在实践中加以检验与调整，促使学生获得更好的发展。

[责任编辑：陈国庆]

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。