《学习场域创新视角下数学活动教学范式建构》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

学习场域创新视角下数学活动教学范式建构

范文

【摘要】为有效解决小学数学活动教学中存在的问题，教师可以从学习场域创新的视角出发，明晰数学活动与学习场域的内涵、学习场域中“四要素”之间的关系、数学活动的类型划分等问题，解决活动教学开展的动力机制及资源素材问题，建构数学活动的教学范式。

【关键词】学习场域；学习场域创新；数学活动；教学范式

【中图分类号】G623.5【文献标志码】A【文章编号】1005-6009（2020）09-0014-04

【作者简介】孙焱，江苏省吴江实验小学教育集团城中校区（江苏苏州，215200）校长，正高级教师，江苏省数学特级教师，“江苏人民教育家培养工程”培养对象。

近年来，在小学数学教学中，大家基本达成了“数学教学本质上是数学活动的教学”这一共识。但在数学活动教学中还存在着一些问题，如活动的形式化倾向明显、活动的氛围和环境的支撑度不够、活动的整体设计不足等。为了有效解决这些问题，墟沟小学于2017年申报立项江苏省基础教育前瞻性教学改革实验项目“学习场域创新条件下的数学活动教学建构”，旨在为小学数学课程的动态化和校本化实施、特色领域的常态化实施以及学生的数学学科素养发展探索出一条有效路径。基于上述实验项目的研究成果，本文谈一谈如何基于学习场域视角建构数学活动教学范式。一、数学活动与学习场域创新

（一）数学活动

数学活动是指在典型的物理空间环境中和特定的关系空间中进行的一种数学探索活动，它是通过动手、动脑“做数学”的一种数学学习活动，具有工具性、操作性、情境性和探究性等特征。这里的“物理空间”和“关系空间”就构成了学习场域。

（二）学习场域创新

本文中的学习场域，是指为学生开展数学活动提供的科学、合理、易操作的物理空间，还指教师、学生、学材、环境之间的关系空间。学习场域创新包括合理物理空间的创新、和谐关系空间的创新、数学活动动力系统及其生成机制的创新。

1.物理空间的创新。

不同的学校可以立足校情有不同的物理空间创新路径。墟沟小学创建了数学学习“1+4”室———改造普通教室，配置实物操作室、模拟探究室、“E”学习体验室和创客教室。

2.关系空间的创新。

关系空间的创新指向学生、教师、学材、环境之间关系的重构———生生之间的“伙伴式”关系，师生之间的“对话式”关系，人与环境、学材之间的“沉浸式”关系，环境与学材之间的“融合式”关系。如教学苏教版二上《我们身体上的“尺”》一课，执教者这样创新学习场域———

生生之间：本节实践活动课，需要学生以小组合作的方式经历测量、比较、交流等活动过程来认识身体上的“尺”，应用身体上的“尺”测量物体，并通过讨论、交流实践过程中出现的问题解决方案来探索数学规律。所以，学生之间的合作能力就显得至关重要，生生之间既要分工明确又要行动统一，根据学生自身的特点来分工合作，注重同伴间的交流、合作以及知识的共享，从而激发学生对数学活动的兴趣，培养学生的语言表达能力。

环境与学材之间：本节课充分体现了数学来源于生活并应用于生活这一理念。身体“尺”主要应用于日常生活中，这就需要本节课的学习与环境充分地整合在一起，利用学习用具、教室、校园等我们身边的一切事物来学习这一内容，使知识不再是遥远而冰冷的文字或符号，而是我们身边活生生的、可充分利用的现实资源。

关系空间的创新不需要面面俱到，可以选取与本节课教学密切相关的几对关系进行创设，且在每一对关系中，选取与活动内容相匹配的基本要求进行具体化设计即可。

3.数学活动动力系统及其生成机制的创新。

基于德裔美国社会心理学家库尔特·勒温的场动力理论，我们认为，数学活动的动力系统由学生主体动力系统、教师主导动力系统和学习场域动力系统三部分构成。数学活动的开展不仅来自各子系统自身的矛盾运动产生的动力，也来源于三个子系统之间相互作用的合力。在学生主体动力系统中，“惯习”为核心，“兴趣”“情感”“经验”为支撑“惯习”形成的三个重要元素。在教师主导动力系统中，“理念”为核心，“认知”“态度”“责任”则是“理念”转化为教学行为的共有力量。在学习场域动力系统中居于核心地位的是“主体活动”，支撑“主体活动”的除了构成学习场域的“物理环境”和“四共关系”（指共生、共享、共鸣、共融关系）以外，还有一个非常重要的元素———“文化氛围”。

数学活动动力系统的运行需要其生成机制来保障。数学活动动力系统的生成机制主要包括合理的活动目标、学生的主体活动以及开展数学活动所需的物理空间和关系空间。学生开展数学活动的动力生成过程，是学生的认知在已有平衡的基础上，在特定学习场域中出现失衡，继而消解失衡达到平衡的动态过程。二、数学活动的教学范式建构及其基本类型

范式是指人们看待与处理特定领域内的一种现象或一系列问题的基本原理。教学范式是指人们对教学这一特殊现象和复杂活动最基本的理解或看法。简单地说，就是人们对教学所做的最基本的界定或解释。从当代教学范式研究的主要成果来看，主要有模仿范式和变革范式两种。模仿范式的学习是以同步学习为中心加以组织，以个人活动为中心加以开展的；变革范式是以合作学习为中心加以组织，以共同体活动为中心加以开展的。从这个意义上来说，模仿范式的学习追求的是效率和效果，变革范式的学习围绕主题展开，追求的是创造性和个性。

（一）数学活动的教学范式建构

基于变革范式的定位与特征，依据“做中学”和具身认知理论，我们建构了数学活动的教学范式“L-H-M”，“L”（Learning field）是指教学的条件———学习场域，“H”（Hands on）是指教學的形式———活动，“M”（Mathematics）是指教学的学科———数学。其基本思想是在学习场域创新的条件下，通过动手做的活动形式开展小学数学教学。其结构模型如图1所示。

图1“L-H-M”数学活动教学范式结构模型

建构数学活动教学范式“L-H-M”，旨在更丰富地获取小学数学活动的主题内容来加以组织，有效激活数学活动动力系统的生成机制，从而引发数学活动动力系统的良性运行。在此教学范式中，重视活动过程甚于活动结果，重视个体差异甚于同一性，最终指向学习场域“四要素”（教师、学生、学材、环境）的共生、共享、共鸣、共融（这也是“四要素”之间的关系空间构建的基本要求）。

（二）数学活动的基本类型及操作流程

小学数学活动课程是根据国家课程设定的目标和任务，是为学生发现数学结论、理解数学知识、验证数学结论而创生、设计的。根据数学活动的目的、应用的知识和选用的工具等的差异，可以将数学活动分为验证型数学活动和探索型数学活动进行研课、辩课，创新和重构数学活动的物理空间和关系空间（如图2）。图2物理空间和关系空间创新结构图

上述结构重在突出“四性”：（1）活动性，无论是物理空间还是关系空间的重构，都围绕数学活动的开展进行；（2）生本性，聚焦学生的发展，突出学生的主体活动；（3）创新性，将数学活动置于创新的学习场域中，创新数学活动开展的动力系统及其生成机制；（4）素养性，学习场域的创新指向核心素养的培养，通过数学素养的落实达成发展学生核心素养的目标。

1.验证型数学活动。

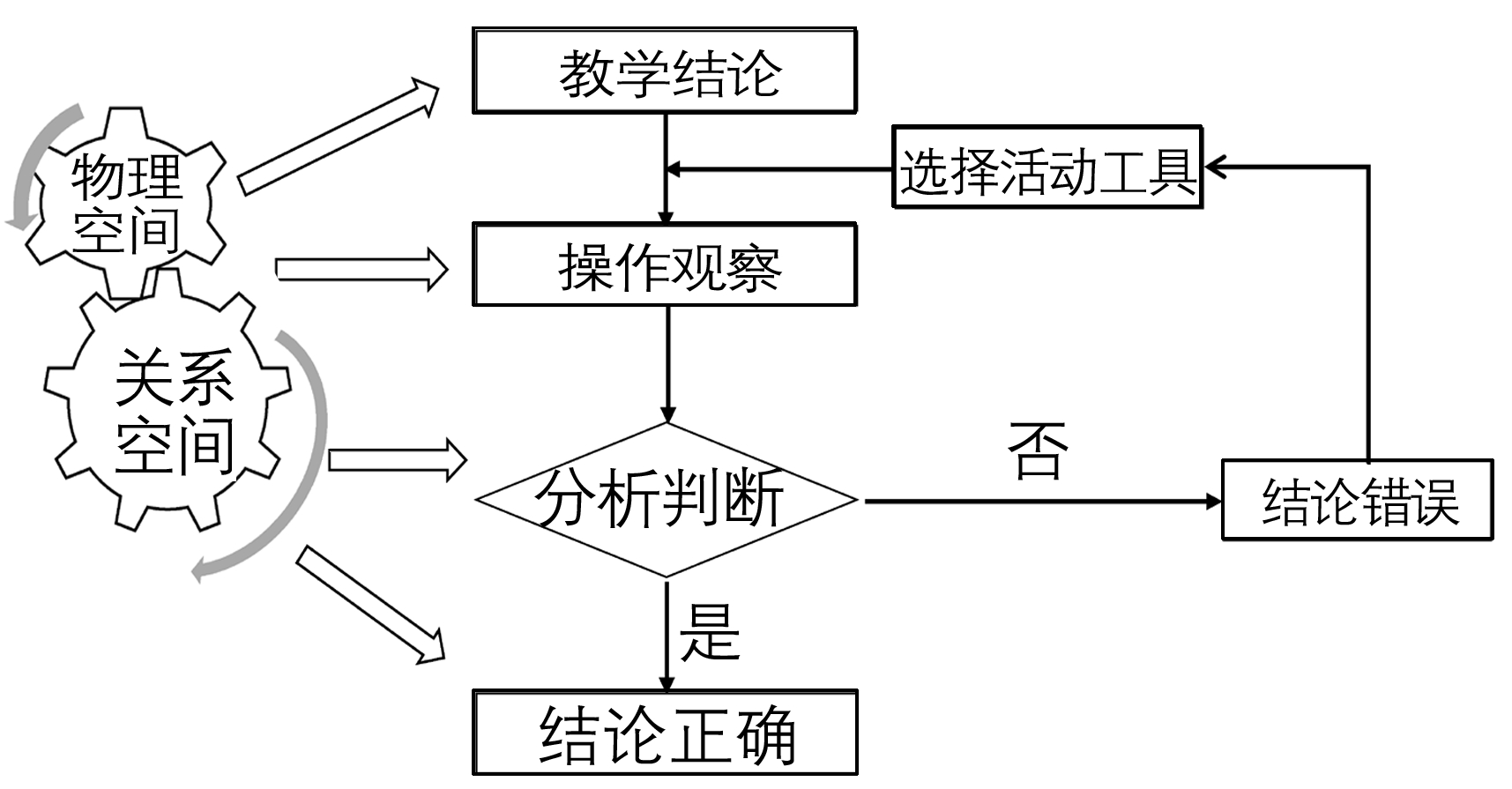
验证型数学活动的教学流程一般如图3所示。验证型数学活动的物理空间主要是指实物操作室和“E”学习体验室，学生通过操作并观察活动过程中的数学现象而获得感性认识，同时由场域的关系空间影响其理性分析，对结论的真伪做出判断。如教学苏教版六上《树叶中的比》一课，执教者这样进行活动设计———图3验证型数学活动流程

活动1：情境导入，引导猜想。

（1）大家课前收集了很多种树叶，请你仔细观察，看看每种树叶有什么特点，并在小组里互相说一说。

（2）你认识这些树叶吗？观察下面的树叶，你有什么想法？

（3）请大家进一步观察这些树叶的大小、形状，把你的想法在小组里和大家分享。

（4）形成猜想，得出初步结论：同一种树叶，形状是相似的。

活动2：操作活动，验证猜想。

（1）两人一组，合作测量10片同一种树叶的长和宽，计算出每片树叶长与宽的比值（得数保留一位小数），并填入第一张表格里。每组测量的树叶种类不同。

（2）计算出你测量的树叶的长与宽比值的平均数，并填入第二张表格里。

（3）观察不同组同学记录的第二张表格，同桌互相说说你有什么发现。

活动3：分析数据，确认结论。

（1）组织比较交流。

（2）确认结论：同一种树叶长与宽的比值都比较接近；不同种树叶长与宽的比值一般不同。

本案例首先引导学生观察，形成猜想；其次让学生利用测量工具进行实际测量，记录数据；然后引导学生对测量出的数据进行分析、比较、交流，进而确定结论。

2.探索型数学活动。

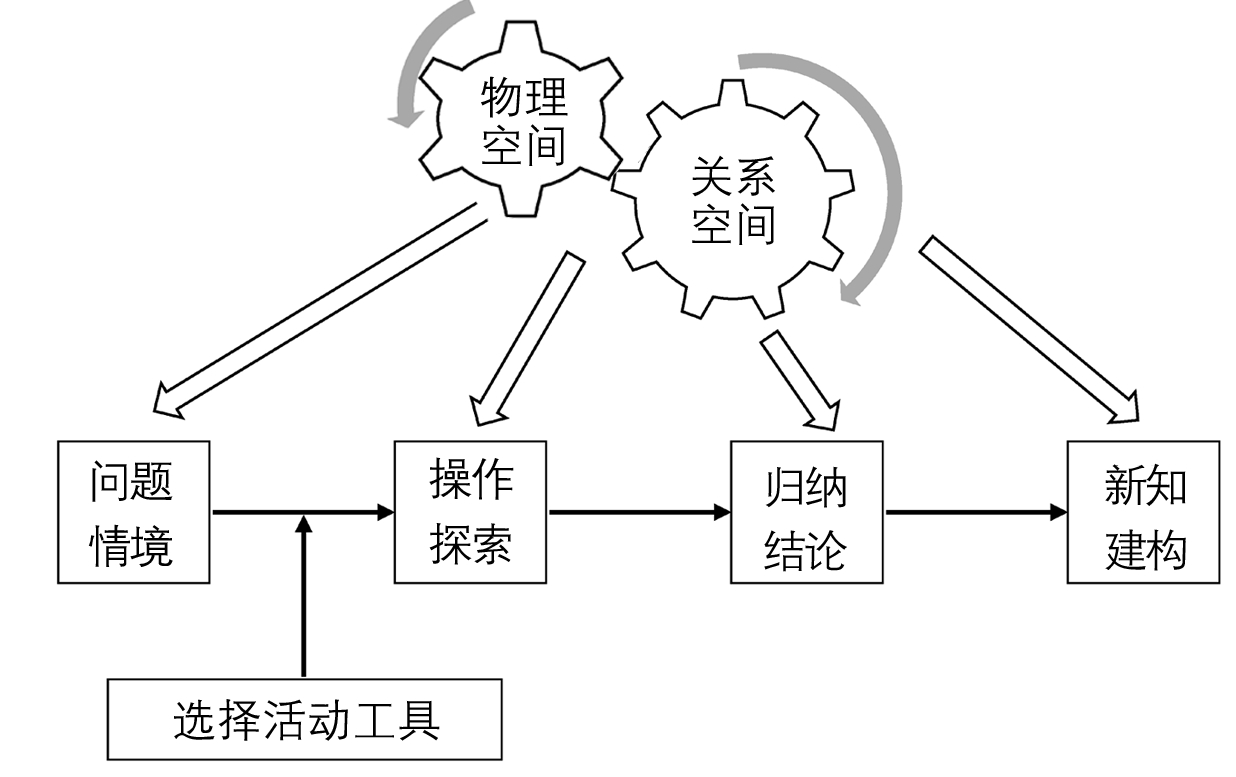
探索型数学活动的教学流程一般如图4所示。探索型数学活动主要利用关系空间的影响创设问题情境，学生在教师的指导下，通过物理空间———模拟探究室进行活动。如教学苏教版二上《有趣的七巧板》一课，执教者这样进行活动设计———图4探索型数学活动流程

首先多媒体展示三角形、平行四边形、正方形的图片。然后引导：同学们认识这些图形吗？这些都是我们学过的图形，如果我们将这几种图形聚在一起，就可以成为数学上一种有趣的玩具———七巧板，用七巧板可以拼成各种美丽的图案。

活动1：第一次探索———简单思考。

（1）一副七巧板由几块组成？

（2）一副七巧板有几种不同的图形？

（3）形状和大小都相同的图形有几组？

学生先独立思考再同桌之间交流，之后请学生分别回答上述三个问题。

活动2：第二次探索———选择七巧板中的2块进行拼图。

小组活动：选择2块图形进行拼图，活动结束后小组代表展示本组拼出的图形。

教师选择用相同图形拼出的拼图和用不同图形拼出的拼图来点评讲解。

活动3：第三次探索———选择七巧板中的3块进行拼图。

小组活动：选择3块图形进行拼图，小组分工合作。

教师从各小组选择不同的拼图投影展示。

在情境创设的基础上，执教者让学生选择七巧板中的若干块（2块到3块）图形通过操作进行探索，并选择有代表性的拼图进行展示，进而引导学生归纳结论，最终建构新知。

在具体实施过程中，数学活动不一定都能概括成这两种类型，也不一定“恪守”這样的操作流程，可以根据实际活动内容、学情等因素进行变化。当然，对于活动类型，还可以从规律探索、思想渗透、思维拓展、模拟实验、动手操作、课外实践、信息技术、课题学习等方面来进行分类和建构。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。