《借图形变换探作图问题》-理学论文，中学数理化论文-论文范文参考-科学狗论文网

标题

借图形变换探作图问题

范文

张磊

[摘要]翻折、平移、旋转与缩放这四种图形的运动，都是图形变换.图形变换的作图包括轴对称作图、平移作图、旋转作图与位似作图.探析图形变换中的作图问题，可以让学生熟悉各种类型的作图方法，明白各类作图的原理;可以培养学生的动手操作能力，让学生直观感受图形变化后位置关系和数量关系的变化，在图形变换的新情境问题中游刃有余.

[关键词]初中数学;图形变换;作图问题

[中图分类号]? ? G633.6? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058（2020）29-0029-02

翻折、平移、旋转与缩放这四种图形的运动都是图形变换.图形变换的引入，使图形运动进入数学课程，要求学生从图形运动的角度看全等三角形、平行四边形、圆等几何图形，由过去的静态几何转变为动态几何.在图形变换里，不仅学习了图形变换的概念、性质与应用，还学习了图形变换的作图，包括轴对称作图、平移作图、旋转作图与位似作图.学生由已知图形作出关于某一直线或某一点的变换图形，能直观感受图形变化后位置关系和数量关系的变化，从而在图形变换的新情境问题中游刃有余.

一、轴对称作图

由已知图形与直线，如何作已知图形关于此直线对称的图形呢？第一步，找出图形中的关键点;第二步，过关键点作对称轴的垂线;第三步，延长垂线，在垂线的另一端取相等的线段，得到对应点;第四步，其他关键点的对应点以此类推，顺次联结各点的对应点.轴对称作图的类型包括在网格图里作已知图形的轴对称图形.在既定图形里以某边为对称轴作轴对称图形;在平面内作已知图形的轴对称图形.

（1）在图1格点中找一点E，由A、B、C、E四点构成的四边形，如果是轴对称图形，那么符合题意的图形有多少个？并写出点E的坐标以及四边形的面积;

评注：作轴对称图形重要的是找对称轴，对称轴可以是水平的、竖直的，也可以是倾斜的，本题的两条对称轴就是一水平一竖直.在已知直线上确定一点，使入射角等于反射角，方法就是找其中一个点的对称点，将另一点与对称点连成直线，所作直线与原始直线有一个交点，这个交点就是求作的点.

二、平移作图

平移作图的一般步骤是：（1）找出图形中的关键点;（2）经过关键点作直线，这条直线要与已知线段平行;（3）在平行线上截取平移距离的长度，得到对应点;（4）顺次联结各对应点得到的图形就是所求作的图形.平移作图的类型包括在网格图中平移作图，在既定图形里平移图形中的一部分，在平面内按指定的方向和距离平移作图，等等.

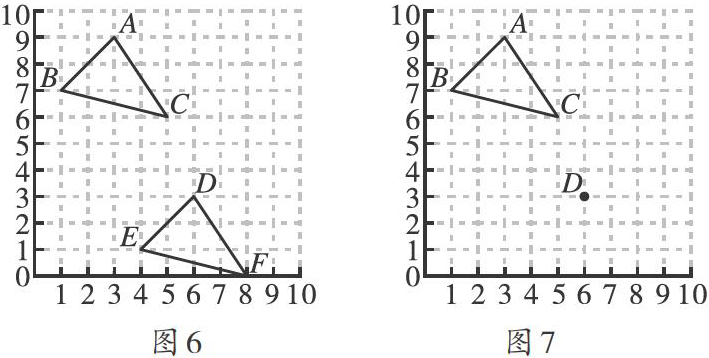
[例2]如图6，三角形ABC可通过平移得到三角形DEF，此时点A落在点D.

（1）请描述三角形ABC经过两次平移后得到三角形DEF的过程.

（2）平移三角形ABC使点B落在点D，在图7中作出平移后的三角形.

分析：（1）先沿水平方向平移再沿竖直方向平移;或者先沿竖直方向平移再沿水平方向平移.△ABC经过两次平移后得到△DEF的过程为第一步向右平移，第二步向下平移，平移的单位分别为3个和6个单位长度;

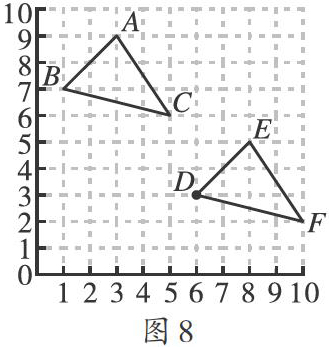
（2）根据点B的对应点是点D，得到平移的方法，再依据平移方法将点A、C平移.如图8所示.

评注：在网格里作图，要充分利用网格里的水平线与竖直线所指示的方向，利用每个小正方形的边长是1的距离，数一数格数就可以确定距离.题中显示了平移作图的两种考法，一是已知平移作图的结果，确定平移的方法;二是已知其中一点平移后的对应点，观察得到平移方法，然后平移图形.

三、旋转作图

旋转作图的一般步骤是：（1）找出图形中的关键点;（2）联结关键点与旋转中心;（3）将连线按要求的方向与角度绕中心旋轉一定的角度;（4）在连线上截取相等的线段，得到对应点;（5）顺次联结各对应点得到的图形就是所求作的图形.

评注：从这里可以看出，旋转与平移的关系，即一次旋转加一次平移相当于一次旋转.轴对称、平移、旋转之间的相互关系还包括如果对称轴互相平行，那么两次轴对称相当于一次平移;如果对称轴相交于一点，那么两次轴对称相当于一次旋转.

图形变换的作图还包括位似作图，即将一个图形放大或缩小，它要求根据相似图形对应边成比例，在经过关键点与位似中心的直线上截取几倍或几分之一的线段.在图形变换作图中，一方面考查了学生的动手操作能力，另一方面也考查了图形变换的性质，因为图形变换的性质是图形变换作图的依据.熟悉各种类型的作图方法，明白各类作图的原理，才能让学生在图形变换的新情境问题中游刃有余.

[? ?参? ?考? ?文? ?献? ?]

[1]? 吴志鹏，陈玉兰.快速作图的四种策略[J].河北理科教学研究，2018（3）：27-29+45.

[2]? 张安军.基于等边三角形的尺规作图下“图形变换”的复习[J].数学教学，2018（3）：14-16.

[3]? 解荣兰. 初中生数学作图能力的研究[D].济南：山东师范大学，2017.

[4]? 仇玉祥.透视中考? 聚焦网格? 巧妙作图[J].新高考（升学考试），2014（2）：48-50.

（责任编辑黄桂坚）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。