《溯源日常提升运算能力》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

溯源日常提升运算能力

范文

孙丽燕

【摘要】运算能力不只是计算技能，更是在运算能力的形成、发展过程中，学生的思维和数学素养得到整体发展。一次抽测的经历，让我们反思：运算能力，教师日常的教学去哪里了？学生表达的日常积累在哪里？学生估算习惯的日常培养在哪里？学生灵活运算能力的形成在哪里？溯源日常，回归本真，为真正促进学生运算能力素养的提升而努力。

【关键词】运算能力算理算法灵活运算日常培养

教育部部长陈宝生指出，教育改革进入了“全面施工内部装修阶段”。不由想到，近年以运算能力作为关键能力考查的抽测，抽测前，“草木皆兵”，练习卷一张又一张，问问邻校，亦是如此。不可否认，临时抱佛脚的练习会有一定作用，但每次抽测前，都需要以停课的代价增强练习强度，来提高抽测成绩，真正是高一级教研部门举行抽测的初衷吗？运算能力，教师日常的教学去哪里了？学生的表达不应该是日常积累的自然呈现吗？学生的估算习惯不应该是在日常培养中自然形成的吗？学生的灵活运算能力不应该是日常意识下的自觉选择吗？溯源日常，回归本真，提升学生运算能力的素养，是教师更应追求的。

一、认识：运算能力培养在课标中的要求

运算能力，作为小学数学的关键能力之一，是历来教学大纲十分强调的。课标指出，运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力还有助于学生理解运算的算理，能够寻求合理简洁的运算途径解决问题。学生能不能依据法则和运算律正确进行计算，是他们运算能力的外部表现。理解算理、寻求合理而简洁的运算途径，是学生的认知程度、思维水平、习惯态度的表现。

课标提出，运算能力的意义不局限于计算及其结果，实际上涉及了学生各個方面的同步发展。教师不能片面追求学生的计算速度，而要提出比较科学、合理的速度要求。计算只有方法灵活、结果正确，才有价值;追求计算的合理与正确，是良好心理品质的表现，需要良好的习惯来配合。

联系学生计算能力调查和计算教学实际，在计算教学中需要多多关注三个方面：处理算理算法的落实，书面和语言的表达，沟通知识和技巧。

二、实践：计算教学的实践追溯

（一）理解算理落实算法，让思维有路径

什么是算理？什么是算法？算理即计算的原理，算法即计算的基本程序和操作方法。算理为算法提供理论依据，是对算法的构建与解释;算法是算理所蕴含行为的提炼与整理，使算理可操作。没有算理的算法是机械的，不成算法的算理不便于操作，不会转化成计算能力。计算教学既要重视算法，也要重视算理。

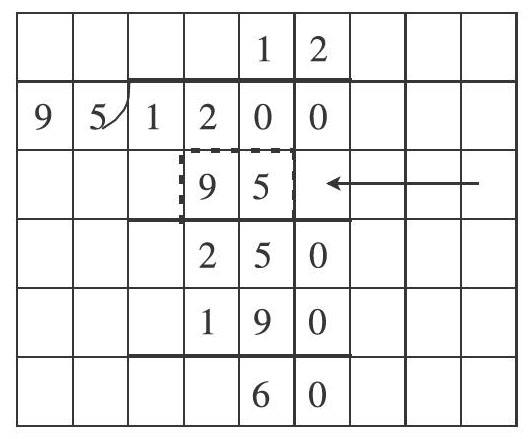
例如，一次抽测中遇到这样一道题：从北京到上海1200千米，一辆货车以每小时95千米的速度行驶，需要多久才能到达？明明用竖式计算出了结果，竖式中的箭头所指的表示的是（）。

A.1小时行驶 95千米

B.10小时行驶 95千米

C.10小时行驶 950千米

D.12小时行驶 950千米

本题得分率为63.4%，考查的是学生对除数是两位数的算理理解。这样的题目得分率应该更高，因为课改以来算理的教学已得到了重视，为什么在教师多次强调的情况下，学生换个情境就不清晰了呢？深层次的原因是学生对除法笔算的基本计算原理还没有产生真正的心理认同，学生只是从外在的形式上浅层次地理解计算步骤，却并不清楚“乘”的操作方法的本质是为了“检查分掉了多少”。所以当学生遇到这样考查思维过程的题目时，往往就会因为理解不清而说不清楚。

1.能在活动中解决实际问题，而形成算理过程比较薄弱

现实的计算教学中，教师能从解决实际问题开始，但是往往不会在直观算理与抽象算法之间架一座桥梁。在学具操作、数形结合的帮助下，学生似乎清晰了对算理的理解。但当学生还流连在直观形象的算理中，马上就面对抽象的算法，运用算法进行计算，思维展开过程匆匆走过场，造成学生没有真正理解算理，出现被动记忆和套用法则的现象。所以，在日常教学中，教师要让学生亲历“动作思维—形象思维—抽象思维”的发展过程。同时又要帮助学生理解抽象计算过程的每一步在具体实际问题中表示什么。让学生在课堂上有充分的自主时间和空间，有充分观察、灵活尝试、展示思维过程、互相补充、辨析评价的机会，真正促进学生思维，理解算理。

2.有算法交流，却经常是点滴的

由学生主动建构的法则一方面要有整体性、条理性，另一方面应该允许儿童味的存在。这样的法则既能控制学生的计算行为，又没有记忆障碍和负担。教师在教学中往往会安排学生总结算法，但形成怎样的法则的思考不够，学生会有什么困难的准备不够，应该给学生哪些帮助的预设不够。教师的教学要实现有层次的培养和渗透内化法则，让学生的计算方法有整体性、条理性，能支持自己的计算行为。

为了学生理解算理、形成法则，上述案例的教学中可以有“一个往返” “一次质疑” “一次反思”。

“一个往返”——从解决问题的步骤形成算式，用解决问题的步骤解释计算过程。

“一次质疑”——思辨这些方法有什么相同、有什么不同，哪种方法方便。

“一次反思”——计算时，要注意什么？除数是两位数的除法应该怎样笔算？

（二）书面和语言表达，让思维可视

语言在运算算理形成过程中有着十分重要的作用。首先，算理是用词或词组来表达的，要借助语言来理解、形成和传递。其次，算理的形成过程是抽象概括的过程，由于语言表达具有重要的提炼功能，所以思想内容经过语言的准确表达之后，增加了迁移的可能性。当然在算理算法形成的各个阶段，语言也会经历“直观语言—概括语言”的过程。

例如，一次抽测中，“判断计算结果是否合理”的两题：

第（1）题：同学们在计算? “753-456”时，出现了如下三种结果，你认为哪两种结果肯定是错的？把你的想法写在得数后面的空格内。学生答案如下：

第（2）题：一篇文章有600个字，小华每分钟打80～90个字，7分钟能打完这篇文章吗？一位同学是这样想的：90×7=630，630>600，所以7分钟能打完这篇文章。你认为这位同学的想法合理吗？为什么？把你的想法写在下面。

答案1：应该不合理，因为小华有可能每分钟打平均数85个字，85×7=595，595<600。

答案2：不合理，因为他只写了最大的，还有一个80没算。

三年级学生得分率仅34%，这些回答都有不同程度的扣分。且不说评分标准合不合理，更主要的是部分学生虽有估算的意识，但语言概括不清楚，答不到点子上。第（1）题学生回答的比较笼统，只说答案一定是错的，没有说明白为什么个位不对或百位不对，故批卷老师就认为他是通过最常规计算得出，得分很少，看不出优化的思维。第（2）题答案1学生是用举反例的方式来表达答案的不合理，没有说清楚小华打字速度为80～90个字，并不是固定打到90个字，7分钟不一定能打完这篇文章，包括答案2也没有说清楚。其实平时教学时讨论过这样的估算实际问题，学生严谨的逻辑思维能力不够，再加之针对性情境练习过少，思维要求高，很多学生说不清楚。教师要引导学生缜密思考，锻炼学生有条理、有逻辑的语言表达能力。

如上图题中，此题得分率为58.5%。此题是分数乘除混合运算，将算式转化为连乘后，先约分再计算即可。但约分和计算这两步一步都不能出错，有的学生在约分时，对于不常见的倍数关系数感不灵敏，如51=17×3，39=13×3，52=13×4，找不到约分的对象;有的学生在连续约分时掌握不够熟练，将整数（39）与分子（51约后的3）进行约分。有的学生书写不规范，尤其涉及整数的约分，由于写的位置不规范，容易把分子当成分母。

1.重视过程展开，关注语言表达

面对实际问题，能灵活选择方法解决，让学生经历解决问题的过程，能用多种方式表达思考过程。学生在灵活运算中语言表达的习惯养成、灵活解决实际问题能力的提升是潜移默化的，是在日常渗透过程中不断地感觉、感知、感受、积累形成的，无形之中，学生思维也得到了发展和强化。

2.培养学习习惯，关注书面表达

计算往往是枯燥的，如果没有积极的情感来支撑，没有良好的习惯相配合，错误很难避免。首先，培养学生追求计算正确的自觉要求和迫切愿望，平时练习的安排要“经常”“量轻”。先要求正确，再适当要求速度。其次，书写工整能减少计算错误，能把情绪调整到比较好的状态（过于追求计算速度，容易导致学生急功近利的心态）。最后，关注每一个学生，对确有困难的学生要加强指导。

（三）沟通知识和技巧，让思维更灵活

不具备计算知识（不懂得运算意义、不知道计算方法）不可能具有计算技巧，知道计算知识未必就有计算技巧，有了计算技巧对计算知识的掌握会达到较高的层次。小学阶段知识主要涉及两个层面的技巧，首先是把客观的计算知识内化成自己的程序性知识，对计算知识的使用正确、计算结果正确（两个正确），然后是应用计算知识的思维灵活、方法灵活（两个灵活）。“两个正确”体现出“扎实”，“两个灵活”体现“水平”。没有“扎实”谈不上“灵活”，没有“灵活”就达不到计算的高水平。

例如下图中所示题目。

本题得分率42%，思维层次比较高的答案是类似答案3：学生能够先找到接近的“51”和“48”或直接发现“48”，再判断48乘12接近600且小于600（值得一提的是答案4的问题2也解答得很巧妙，通过估算，敏锐地发现48×12与50×12相差2×12，故直接用12×2求出找回的元数）。答案4：根据付600元买12份奖品，用除法算出每份奖品可以用50元钱，从而得出买每本48元的字典。而这样的学生并不多，还有一部分学生逐一计算后判断（答案1）;很多学生有估算意识，但不能敏锐地通过目测先自然淘汰相差太大的文具盒和书包，还是逐一進行了估算（答案2），当然也不排除有的学生可能是不知如何表达不选文具盒和书包的理由，所以把四种文具估算的过程逐一写了出来，但确实还有很多学生缺乏这样的敏锐的数学眼光。

运算能力的形成，往往反映在学生能正确地选择合适的计算方法来合理灵活地解决实际问题上，但很多学生习惯于以精确计算、逐一排除的方式来解决问题，灵活思维不够。很多学生的综合选择信息能力、灵活选择算法能力还有很大的发展空间。

1.灵活思维培养，关注选择、判断、灵活运算能力的落实

灵活使用运算知识主要是利用运算律、运算性质、积或商的变化规律进行简便计算。合理选择计算形式，能够口算则口算、需要笔算就笔算、可以估算应估算。能够根据运算的意义、各种形式的数的改写，把一种计算转化成另一种比较简便的计算，包括联系数感的计算技巧，实现保底要求，渗透高标要求。引导学生要先思后算，对计算过程进行合理的规划、对计算结果进行必要的反思，选择合理、简洁的算法，灵活运算的要求要贯穿始终，并且通过过程中的拓展提高学生对数的敏感度，尽可能在解决生活密切相连的问题中实践体会，处处关注落实选择、判断、灵活计算能力培养，增强思维的灵活性，使运算灵活作为学生的自觉要求。

2.关注针对性练习设计，渗透方法积累经验

计算知识转化成计算能力需要必要练习，更要注重练习质量。精心选择和设计的练习，不仅是教给学生知识与技能，更重要的是通过练习实践，培养学生的能力，发展学生的智力，启发、开拓学生思路，激发学生的学习兴趣。尤其是精心设计的开放性练习，在注重数学方法、数学思想的渗透的同时，学会把思考过程表达出来，灵活选择更优的方法。

“打铁还得自身硬”。要培养学生的数学素养，教师本身必须具备深厚的数学素养，切实变教学理念为教学行为。理解算理落实算法，让思维有路径;书面和语言的表达，让思维可视;沟通知识和技巧，让思维灵活。溯源日常，促进学生运算能力的提高，数学素养的综合提升。

【参考文献】

杜娟.提高小学数学计算教学有效性的方法探析[J].数学学习与研究，2019（7）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。