《巧借几何直观优化数学教学》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

巧借几何直观优化数学教学

范文

张永勤

[摘要]数学教学中，教师巧妙借助几何直观来帮助学生理解概念、理解算理、解决问题等，可以促进学生探究的深入，不断优化学生的数学学习，提升学生的数学学习质量。

[关键词]几何直观;优化;数学教学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）24-0029-01

几何直观是《数学课程标准》（2011版）提出的十大核心概念之一，指利用图形描述和分析问题。数学教学中，教师巧借几何直观可将抽象的数学知识直观化、形象化、简单化，降低学生理解的难度，提高数学教学效率。那么，教师如何借助几何直观引导学生进行数学学习呢？

一、借助几何直观理解概念

数学概念是学生学习数学的基础，而小学生的思维正处于从具体形象思维向抽象逻辑思维过渡的发展阶段，所以抽象的数学概念对学生來说有一定的理解困难。数学课堂中，教师如能依据几何直观的特点，把抽象的数学概念与直观的图形有机地结合在一起，可以帮助学生更好地理解数学概念。

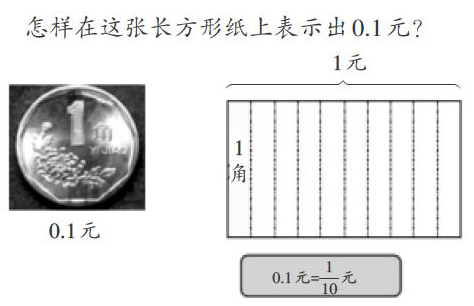
例如，教学《小数的意义》时，由于小数的概念比较抽象，教师如果直接讲解的话，学生难以理解小数的意义。那么，怎样才能帮助学生真正理解小数的意义呢？教师可从学生已有的知识经验出发，如“1元等于10角”等，让学生明白小数之间的进率关系。然后教师提问：“1元等于10角，如何用小数来表示？”学生很快回答：“可以用0.1元表示。”“这是为什么呢？”这时，教师可借助直观的长方形（如右图）来帮助学生理解，即把一个长方形平均分成10份，其中的一份就相当于1角。这样教学，形象直观，使学生深刻理解小数的意义。

上述教学，教师从学生熟悉的元、角、分入手，借助长方形让学生感受小数与分数之间的联系，使学生在直观中理解小数的意义，提升了概念教学的质量。

二、借助几何直观理解算理

计算教学中，理解算法算理是基础。那么，怎样才能深化学生对算理的理解呢？借助几何直观可以让算理直观地展示在学生面前，使学生易于理解与接受。

例如，教学《乘法分配律》时，大多数教师都是根据教材例题，按照分析题意、列式解答、讲述思路、观察比较、总结规律的过程进行教学，这样导致部分学生出现理解困难。因此，教师不妨借助几何直观，将乘法分配律与长方形的面积相结合（如右图），使学生对乘法分配律的理解更加深刻。

由此可见，在计算教学中，教师巧妙借助几何直观引导学生理解算理，不仅能把复杂的数学问题简单化，而且可以让学生的数学学习更轻松，使学生真正理解与掌握所学知识。

三、借助几何直观解决问题

解决问题时，有些学生在理解题意方面存在一定的困难。因此，数学课堂中，教师可借助几何直观来帮助学生理解题意，降低学生的解题难度，提升学生的解题能力。

例如，教学《比一个数多（少）几的数是多少》时，有这样一道题：“小华扎了11朵红花，比小芳多扎了3朵，小芳扎了几朵红花？”对于这类问题，学生容易出现的错误就是看到“多”字用加法求解，看到“减”字用减法求解。那么，怎样才能避免学生出现此类错误呢？借助几何直观来帮助理解是一个有效的途径，教师可让学生根据题意画一画。在教师的启发下，有的学生用○来表示小华和小芳扎红花的数量（如下图），即先画出小华扎红花的数量，再根据题意画出小芳扎红花的数量。通过直观的图示，学生可以清楚地看到小华扎的红花多，小芳扎的红花少，所以小芳扎的红花为11-3=8（朵）。这样教学，使学生轻松理解题意，达到解决数学问题的目的。

小华：○○○○○○○○○○○

小芳：○○○○○○○○

由此可见，在解决问题教学中，教师可充分利用几何直观的优势，引导学生想一想、比一比、画一画，这样可深化学生对题意的理解，降低学生的解题难度，提升数学教学质量。

总之，数学教学中，教师应根据具体的教学内容，适时运用几何直观来帮助学生理解概念和算理、解决问题等，这样可以化抽象为直观、化繁为简，提高学生解决问题的能力。

（责编杜华）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。