《莫让“未卜先知”架空操作效力》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

莫让“未卜先知”架空操作效力

范文

刘亚东

[摘要]自己动手得出的结论是最有说服力的，也是最有科学效力的，但是对于一些显而易见的定理，学生通过预习早已能直接套用其形式，带着未卜先知的结论去操作，学生就会投机取巧，架空操作的效力。教学 “三角形的内角和定理”时，教师通过调研分析的结果改良教学，取得了很好的教学效果。

[关键词]操作;三角形的内角和;测量

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）05-0021-02

三角形的内角和定理是深入研究三角形的理论基础。课本先让学生测量各类三角形的内角，分别计算出各类三角形的内角和，再自主猜想任意三角形的内角和都为180°，接着指引学生用拼接法来证实猜想，进而得出确切结论。由于该内容非常适宜操作验证，因此它成了许多教师展示课的首选，然而操作起来却意外频发：如让学生用测量角度的方法探寻三角形内角和规律时，学生都说是180°，鲜有179°或181°等情况出现，导致教师找不到反例，也没有可以对照辨析的错误资源。

一、教学实录

师（课件展示3个三角形，形状分别是钝角三角形、锐角三角形与直角三角形）：凭肉眼观察，哪个三角形的内角和最大？

生1：我觉得它们3个的内角和是相等的。

生2：我也同意这种说法，因为已知四边形的内角和是360°，将四边形沿对角线切分，得到2个三角形，就能顺利得出1个三角形的内角和就是四边形内角和的一半，也就是180°。

师：任意1个三角形都能通过分割四边形得出吗？每个三角形的3个内角都一样吗？

生（齐）：不是。

师：那怎么求出其内角和呢？

生3：测量。

师：怎样量呢？

生4：用量角器量。

师：老师有个要求，就是每位组员可以自由发挥，绘制一个不限形状的三角形，精确测得各个内角的度数后，如实记录数据。

师：测量要实事求是，不准弄虚作假。4分30秒后开始汇报。

生5：我画的是1个钝角三角形，钝角度数为170°，其余两个锐角的度数各是5°和5°，合计180°。

生6：我画的是1个直角三角形，毫无疑问，直角当然是90°，其中一个锐角是45°，另一个锐角也是45°，三个角相加为180°。

生7：我画的是1个锐角三角形，三个角全是锐角，度数各是80°、34°、66°，三个角相加也是180°。

生8：我画的也是1个直角三角形，直角当然是90°，剩余两个是锐角，各是58°和32°，3个角相加也是180°。

师：同学们真是手脚麻利！通过亲自测算，发现了一个重大秘密，那就是任意一个三角形的内角和均为180°，有没有与180°不同的结果呢？

生（齐）：没有！

师：真的没有吗？

生（齐）：没有！

师：我发现一例。请这位同学来说说他的读数和计算结果。

生9（慢吞吞地）：我量的3个角的大小各是110°、34°、34°，三个角相加为192°。

師：不对吧！110°+34°+34°=192°吗？应该是178°吧。

师：其他同学有不同结果吗？

生（齐）：没有！

生10：我怀疑他量错了。

师：今天我们能将所有三角形全部画出来检测吗？（不能）我们班有多少人？（48人）三角形千千万万，不计其数，各种形状应有尽有，内角和是否都是180°呢？有没有例外？

生（齐）：没有！

生11：我怀疑生9画三角形时，一个角没有连接密实，以前我也犯过这种错误，但是量的结果都是180°。

师（欣喜地）：同学们，测量误差在所难免，得到的数据和结果相应地就会失实，看来用量角器测量也有缺陷，接下来我们撤除量角器。弃用量角器后，能改用其他方法证实三角形的内角和是180°吗？

……

二、调研分析与改良措施

1.调查分析

学生测算的结果出奇地统一，都为180°，当真是“人人得手”吗？笔者对四年级两个班110位学生进行了两次调研。

第一次是让学生分别测出图1左端单列的6个角的大小（其中∠1、∠2、∠3与①号三角形的三个内角大小吻合;∠4、∠5、∠6与②号三角形的三个内角大小吻合）。

第二次是让学生测出图1右端的①和②号两个三角形的三个内角的大小。

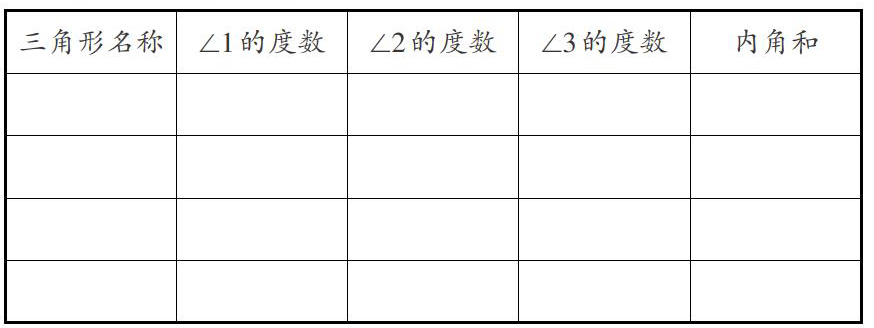
度量结果如下表：

由此分析，第一次测量结果科学可靠，有18位学生量得①号三角形对应内角的和为180°;有23位学生量得②号三角形对应内角的和为180°，得出两个都是180°的有6位学生。有些学生尽管测算得到180°的角度总和，但是具体到每个角的度数还是存在微小误差。第二次测量的结果可信度很低。有些学生投机取巧，只量出两个内角的度数，再用预知的总和180°作差，推算出第三个角的度数。这种因果颠倒、循环论证的做法，归咎于学生测量前预先知道三角形内角和为180°的定理。如果操作得出的与这个理论的结果有出入，为了掩盖失误，逃脱责罚，学生就会偷偷篡改实验数据。因此，在课堂教学中，尤其是公开课上，很少有学生愿意丢丑露拙，会极力否认自己测的不是180°。有些学生则为了迎合老师，也会违心地说出自己测量的结果是180°。

2.改进策略

师：请大家完成课堂练习第1题（量出图1中的6个角）。认真测量，不得有误，测量后汇报（先汇报∠1、∠2、∠3三个角的度数，再汇报∠4、∠5、∠6三个角的度数）。

生1：∠1=54°，∠2=80°，∠3=48°。

生2：∠1=52°，∠2=79°，∠3=50°。

生3：∠1=50°，∠2=80°，∠3=50°。

生4：∠1=55°，∠2=80°，∠3=79°。

生5：∠4=40°，∠5=110°，∠6=35°。

生6：∠4=40°，∠5=106°，∠6=35°。

师：方才我们测量的∠1、∠2、∠3的大小与①号三角形的三个内角相吻合;∠4、∠5、∠6与②号三角形的三个内角相吻合（课件动态演示），请大家再次测算它们的內角和是多少？

（学生计算后汇报;全班约有75%的学生没有得到180°，但是基本都在175°与180°之间;个别学生读数时，张冠李戴，得到200多度的结果）

师（指着课件上的两个三角形）：为什么我们测算的结果五花八门呢？

生7：可能是读数失误。

生8：也可能“两点”（量角器的中心点与角的顶点）未能严格对准，“两线”（量角器的0刻度线与角的边线）没有重合……

师：在度量的时候，微小的误差在所难免。那么，除了测算，你还有别的方法来证实三角形的内角和是180°吗？

……

三、让动手操作成为一种心甘情愿之举

学生已经提前获知三角形的内角和是180°这个结论，再让学生去测算三角形的内角和，只会使学生丧失操作的兴趣和动机，就会有一些学生投机取巧，违规操作，量出两个角的度数后，推算出第三个内角的度数，假冒是测量的结果;一些学生眼见得不到180°，于是进行重新测量，东拼西凑，削足适履，勉强得出180°。这样一来，动手操作就形同虚设。因此，笔者在两次调查分析的基础上，调整思路，改进教学设计：没有固执地要求学生量三角形的三个内角，而是先把三角形的三个内角分割出来，让学生尽兴“盲测”，再揭晓真相——它们分别对应三角形的三个内角，这样的操作迫使学生只能老老实实测量度数，按部就班计算角度和，并且意识到不认真操作得不出180°这个结论，断了他们弄虚作假的后路，从而激发了他们另辟蹊径的决心，调动他们寻觅其他验证方法的积极性与主动性，操作的必要性呼之欲出。

有的学生把矩形分割成两个全等的直角三角形，推知内角和是180°;有的学生利用三角板的固有度数，计算内角和;有的学生分别在钝角三角形、锐角三角形内作高，分割成两个直角三角形，推理出其内角和也是180°……在此基础上，只需要引导学生大胆想象：如果把三角形的三个内角剪切下来，拼接在一起，会得到什么角呢？这样，师生自然配合默契，合作愉快。

因此，操作材料要精耕细作，只有打造精品，才能让“动手”成为“甘心情愿”，甚至“求之不得”之举。

（责编金铃）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。