《基于线性回归的中学生备学科成绩相关性分析》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

基于线性回归的中学生备学科成绩相关性分析

范文

商卓然

【摘要】本文通过利用Excel软件，对初二、初三两个年级学生的数学成绩与物理、化学成绩进行线性回归分析，探究中学生数学成绩与物理、化学成绩的相关关系。

【关键词】线性回归;最小二乘法;各科成绩;相关关系

一、提出问题

数学作为一门基础学科，在自然科学体系中占有极其重要的地位。提出问题：数学作为中学阶段的三大主科之一，对其他学科尤其是物理、化学学科的学习起着很强的带动作用。那么，中学生的数学成绩与物理、化学成绩究竟有着怎样的相关关系呢？

二、建模准备

1.为了科學地分析中学生数学成绩和物理、化学成绩的相关关系，结合高中数学统计部分的相关知识，掌握了对两个变量进行线性回归分析的知识和方法，为建立模型提供了理论基础。

2.搜集了我县初二、初三年级某年全县统考的总成绩单，并剔除了缺考人员的成绩。初二年级样本总数为7328，初三年级的样本总数为7412。庞大的样本数，保证了研究的客观性和准确性，增强了研究结果的说服力。

3.自学利用Excel软件进行线性回归分析的方法，为建立模型提供了计算机这一强大的武器。

三、建立模型

根据所学知识，设线性回归方程为y =bx+a，式中，a-b由最小二乘法求出：

变量间相关性的强弱可由|r|定性判断：

根据上述公式，利用Excel软件自动计算a-b和，，即可确定线性回归方程，绘制回归直线，并分析变量间相关性的强弱。

1对初二年级数学成绩与物理成绩的相关关系进行分析

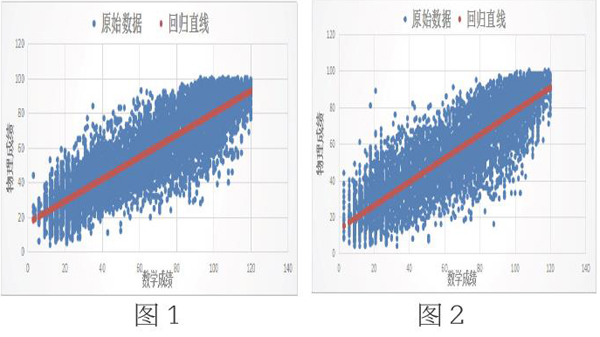
作出散点图和回归直线，如图1所示，回归直线方程为：y=0.63x+16.44，相关系数r=0.873，处于（075，1）区间内，说明两变量之间存在很强的相关性。

2.对初三年级数学成绩与物理成绩的相关关系进行分析

作出散点图和回归直线，如图2所示。回归直线方程为：y=0.65x+13.04，相关系数r=0.879，处于（0.75，1）区间内，说明两变量之间存在很强的相关性。

3.对初三年级数学成绩与化学成绩的相关关系进行分析

作出散点图和回归直线，篇幅限制，这里图略去。

回归直线方程为：y=0.58x+25.88，相关系数r=0.857，处于（0.75，1）区间内，说明两变量之间存在很强的相关性。

综上，中学生数学成绩与物理、化学成绩之间存在较强的相关关系，数学是其他自然科学的基础，学好数学，对于其他自然科学的学习具有促进作用。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。