网站首页  词典首页

请输入您要查询的论文：

　

标题 浅谈算法思想在高中数学教学中的渗透
范文 张英斌
摘 要： 从高中数学模块复习时知识点归纳教学、概念与公式教学、教学难点突破、解题方法指导教学等四个方面来谈算法思想在高中数学教学中的渗透，从而培养学生思维的条理性，体会数学是具体的、简单明了的及可操作的，进一步提高学生对数学学习的自信心.
关键词： 算法思想；渗透；高中数学教学；框图
《普通高中数学课程标准（实验）》指出：算法除作为本模块的内容之外，其思想方法应渗透在高中数学课程其他有关内容中，鼓励学生尽可能地运用算法解决相关问题 [1 ].在高中数学课程中，许多数学问题都蕴含了丰富的算法思想， 因此，在数学教学中我们可以培养学生利用算法来解决数学问题的思想意识.下面通过四个方面谈一谈算法思想在高中数学教学中的渗透.
1 在高中数学知识点进行梳理的过程中渗透算法思想，可加强知识结构的系统化、条理化
高中模块复习时将知识点通过框图进行呈现，使知识结构系统化、条理化，便于学生记忆.例如对数列这一模块知识的复习教师可先用框图来展示（如图1）：
然后学生再根据这个框图把相关知识点补充完整，这样就能把这部分的知识深深地映在脑子里，不容易忘记.
2 在高中数学基本概念、公式教学中渗透算法思想
某些数学概念定理也蕴含着算法思想，例如在《统计初步》一章里书本在介绍系统抽样这个概念时，就可用算法框图来描述（如图2）：
这样用框图来表示让学生理解和应用起来更加直观高效.数学公式本身其实也是一种算法，例如在学习离散型随机变量的方差时，学生感觉公式难记，容易忘记，教师可以引导学生写出算法编出程序，现编程如下（如图3）：
学生再根据算法，尝试用计算机动手操作执行，公式就不容易被忘记，学生学习数学的积极性也能被调动起来.
3 在教学中适当渗透算法思想，能更好地突破教学难点，简化教学过程
如在二元一次不等式的解法教学中，可以渗透算法思想，算法框圖如下（如图4）：
又如数列{an}的前n项和Sn用倒序求和可以用算法来描述：第一步，判断与首末等距离的两项和都相等吗？若是，执行第二步，否则考虑其它求和方法并结束算法；第二步，把前n项和倒序书写，即Sn=an+an-1+…+a1再与原Sn=a1+a2 +…+an相加，可得Sn=，结束算法.再如利用导数研究函数f（x）=xlnx的单调性，可用以下算法框图来总结解题步骤（如图5）：
用算法框图来描述，步骤清晰，过程直观明了，这样学生理解起来更容易，从而能更好地突破教学难点，达到事半功倍的效果.

4 在高三总复习解题方法指导教学中渗透算法思想，可更好地发展学生思维的条理性与表达能力
在高三总复习中，我们常遇到方程有解或不等式恒成立求参数范围这类问题，这类题型算法步骤清晰，可以用算法来归纳总结.如已知f（x）=xlnx，g（x）=-x2+ax-3，2f（x）≥g（x）对一切x∈（0，+∞）恒成立，求实数a的取值范围.
这是高中数学中常见的题型，可以用算法归纳如下：
第一步，把含参数a放式子一边，其余放式子另一边，即等价于a≤x+2lnx+在x∈（0，+∞）恒成立；
第二步，记函数h（x）= x+ 2lnx +，利用导数求出最小值h（x）min=h（1）=4；
第三步，下结论，对x∈（0，+∞），2f（x）≥g（x）恒成立时，实数a的取值：a≤h（x）min=4.
如果参数a放一边较难实现，可转化成二次函数求最值或再用导数求最值.如已知函数f（x）=lnx+ax-a2x2（a≥0）.若f（x）<0在定义域内恒成立，求实数a的取值范围.

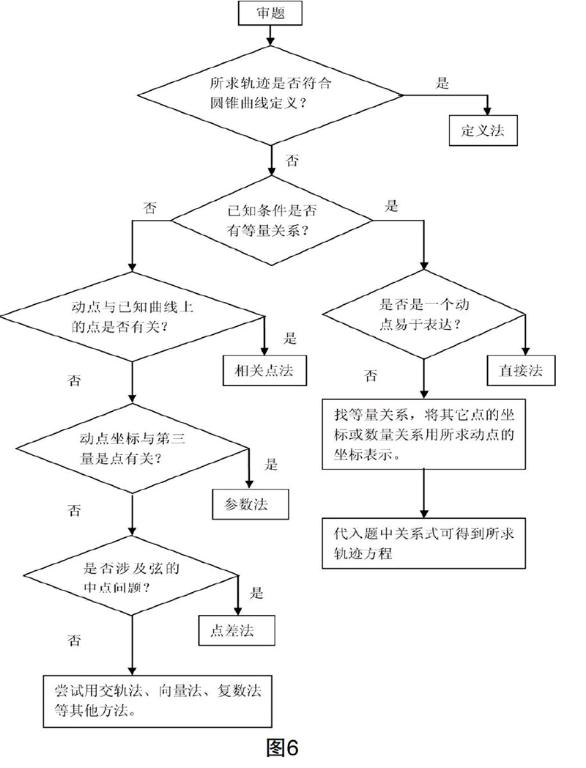
到了高三总复习，对解析几何这一部分，在解这类题时学生依旧感觉棘手，不会分析，考试时经常放弃.其实，解析几何在解决思路和方法上还是有步骤可循，可引导学生将其分类整理成相应的算法.如对圆锥曲线轨迹的求解，方法众多，可以用算法帮助学生掌握求轨迹方程的解决方法，使学生养成良好的思维习惯（如图6）.

在高中数学教学中渗透算法思想，可以更好地发展学生思维的条理性与表达的能力，让学生更好地体会数学是具体的、简单明了的，是可操作的，可以把实际问题编写出程序让机算机来实现，从而培养学生对数学的兴趣，降低学生对数学的畏难心理，提高学生的数学自信.

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（实验）[S].北京：人民教育出版社，2003.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 19:54:09