《思前想后，让知识点生根发芽》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

思前想后，让知识点生根发芽

范文

李丽琼

【摘要】思前，指教育者引导学生思考并整理以前学过的与本课相关的知识;想后，指教育者事先要预设学完本课，要为后面将要学的知识做好准备.数学本质是指数学的内涵，既表现为客观事物背后的数学知识、数学规律，又表现为隐藏在数学知识背后的原理和本质属性.发散思维，指能由一个点引发很多与之相关的联想，在解决问题时能从多方面、多角度去思考的思维方式.本文从纯数学知识点教学现状切入，分析了当前数学知识点片段式教学现象，提出在教学时要把握数学本质，把知识点的前世、今生、将来纳入考量之中，并让学生从多角度，用多种方法去经历知识点的来龙去脉的教学构想.

【关键词】思前顾后;发散思维;片段式;系统化

在我们学校有一位前辈，四川人，50多岁，好像初中学历，普通话不怎么标准，教英语，在20世纪80年代，农村很缺老师，她是那时来学校教书的.从教以来，她就是我们学校的神话，她所教班级学生的学业水平高出其他班一大截！她曾说：“我没什么学历，我要向你们年轻人学习才对！我上课没什么规划，有时看到一个知识点想到哪就讲到哪.”她的这种看似随意的教学方式，不就是由一个知识点，联系与之相关的知识，形成知识网络的实例吗？孩子们头脑中的知识不是零散的、点状的记忆，而是根深于知识网中的，长此以往，能很好地培养学生的发散思维能力和整理与复习能力.

其实数学学科更注重知识点的前后联系，要想学好数学，更应注重知识体系的完备.可我们平时教学，常常只管例题中的那一个知识点，忽略了知识点的前后联系.

目前，苏教版的小学数学教材，多是块状的，知识点分散.比如有关分数的知识：三年级，初步认识分数，同分母分数相加减;五年级，分数的意义，约分、通分，异分母分数相加减;六年级，分数乘除.在平时教学中，有的教师一直教低年段，有的教师一直教高年段，对于教材知识点的走向和要求以及后续了解得不够，在教学中会存在照本宣科、缺少前后联系的现象.

一、就例题教例题的单个知识点教学

德国著名数学家和教育家克莱因倡导“高观点教学”：指从高等数学的角度来审视初等数学.而我们在教学中就题论题，只看到单一的知识点，割裂了知识点的前世与未来，呈现的是“掐头去尾”式的知识点.

一次听新教师上“5的乘法口诀”一课，该课的教学目标是“会背乘法口诀，会用乘法口诀”.此教师由5个5个数导入，然后根据数的过程，把口诀填写完整，填完口诀，先自己背诵，同桌互背，指名背，然后做跟5有关的乘法巩固练习，最后以背诵口诀结束此课.

1.缺少了整体视野的零散知识

此节课看似环环相扣，同学们口诀也背熟了，题目也会做了.但缺少了：①乘法口诀的来历.②我们为什么要学乘法口诀.③乘法口诀在什么时候使用.④乘法口诀是如何推导出来的.⑤除了乘法能用乘法口诀，还有哪些地方也能用乘法口诀.这5个问题都是此节课要思考的有关乘法口诀的本质问题.

2.缺少了从头到尾经历知识点的产生与形成的过程

乘法是求总数时的简便计算，当几个相同加数相加时，可以改写成乘法来算.就这节课而言，其实五的乘法口诀的编写，从5个5个数引入看似没有问题，但数一次就把口诀填写出来，略显单薄，总觉得对知识点的经历和感悟还不够充分.我认为应该从生活实践中引入.例如，一只小船能坐 5人，求有2只、3只、4只、5只小船时共有多少人？其实乘法口诀是用加法推导出来的，5+5=10（2个5相加是10，二五一十），5+5+5=15（3个5相加是15，三五十五），5+5+5+5=20（4个5相加是20，四五二十），5+5+5+5+5=25（5个5相加是25，五五二十五）.

3.忽略了知识点的延伸与生长

本节课只是背了5的乘法口诀，做了和乘法相关的练习题，其实乘法口诀不光用于乘法计算，本节课忽略了知识的拓展与延伸.其实只要简单出示几道变式练习，这节课就会丰满很多.如：

1.20-5-5-5-5=（）

2.如果有6条船，一共有几人呢？你会用不同算式解答吗？

3.如果老师有10块糖，要分给2个小朋友，每个小朋友一样多，每人分（）块.

这样学生对乘法口诀的认识会深刻很多，同时为口诀“五六三十”、平均分、除法的学习埋下伏笔.

二、思前顾后，让数学知识点生根发芽

特级教师周卫东在《试谈高观点视角下的小学数学教学》中曾指出：站在学科结构和学生认知结构的宽度，小学数学教学要大概念统领，教学时要能看到深层的思想方法，教学时应该能看到数学知识的内在结构.

《小学数学有效教学》一书中也指出：把握数学本质+研究学生=有效教学.

本文阐述的是基于他们的思想下的教学探索.

1.从零散的知识点教学转向结构化教学设计

以“5的乘法口诀”教学为例，在教学之前教师要思考与这节课相关的所有知识点.在教学“5的乘法口诀”时，不仅仅是5的乘法口诀的背诵与应用，应该将知识点扎根于加法与乘法的联系，要将乘法与每次减去相同减数的减法，乘法与平均分（除法）联系起来.这样才会让学生习得的知识既有根可寻，又能得以延展.

2.从片段式习得转向“从头到尾”多种方式自己经历习得知识

以五年级的“小数的意义”为例.教师让学生从2.1，53，100，0.5，0.35中找出小数，然后让他们说说小数和整数有什么不同，引出小数点.然后讲53中的5代表5个十，0.5中的5代表5个十分之一，0.35中的5代表5个百分之一;2.1中的1代表1个十分之一，100中的1代表1個百.最后做相关的巩固练习，学生谈学习收获，结束.

对于这位新教师上的这节课，我觉得她让学生经历的还不够，对小数的来龙去脉介绍得还不够深入.

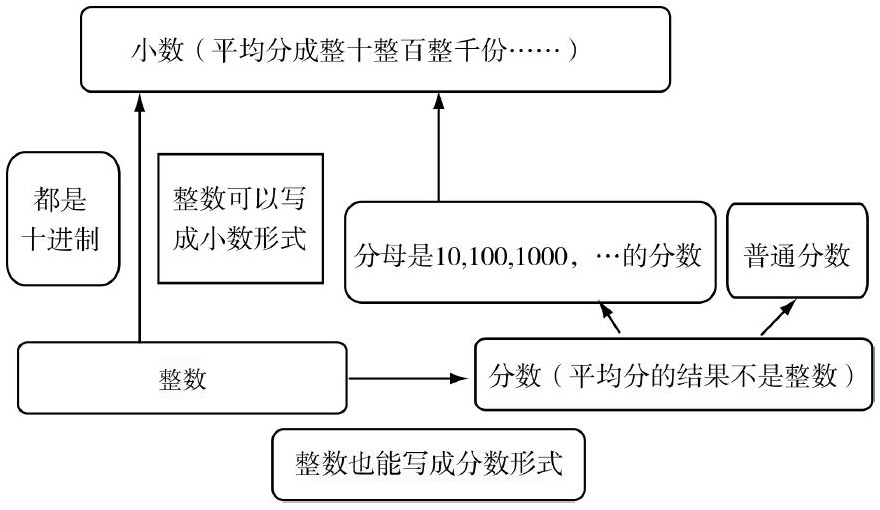
如果由我来上这节课，课前我会整理出跟小数有关的所有知识点，课上我会让学生总结一下我们认识了哪些数字形式，接下来我会让他们自己去寻找这几种形式间的联系.如下图：

让学生结合直观图来认识：10个0.1是1，10个 0.01是0.1，10个0.001是0.01，让学生感悟小数点后面的数位依然是“满十向前进一”，然后我会让学生在计数器上数数，感受“满十向前进一”，最后在数轴上感悟小数的“十进制”.

3.從戛然而止转向为后续学习埋伏笔

课的最后教师问：“这节课你们有什么疑问和困惑吗？”学生的问题天马行空，这样的结尾不好把控，但思维含量丰富.这需要教师从全局去把握数学知识的本质.我们可以在课的最后以练习题的方式拓展.如小红和小明一共有10元钱，爸爸再给小红2元，小红就有5元了，小红和小明各有多少元钱？再如路程、时间、速度之间的关系等生活中的数学问题也可以用来拓展.

三、思前顾后的课堂教学策略

在实际的教学中，我们常常是就题讲题，同学们学的知识点是散点式的，不成网络和模块，不成知识系统，不利于学生记忆和掌握，所以在高观点教学、深度教学的观念指引下，在数学教学应该把握数学本质的理念影响下，得出数学的每个新知识点的习得要“思前想后，把知识点放到知识体系当中，同时做好延伸，为后续学习埋下伏笔”.

（一）对知识点进行思前顾后，培养学生的发散性思维

布鲁纳曾说过，任何学科都有它的基本结构.数学不是知识点的简单堆砌，它是很多知识之间的交错融合，不可随意割裂其内在联系.

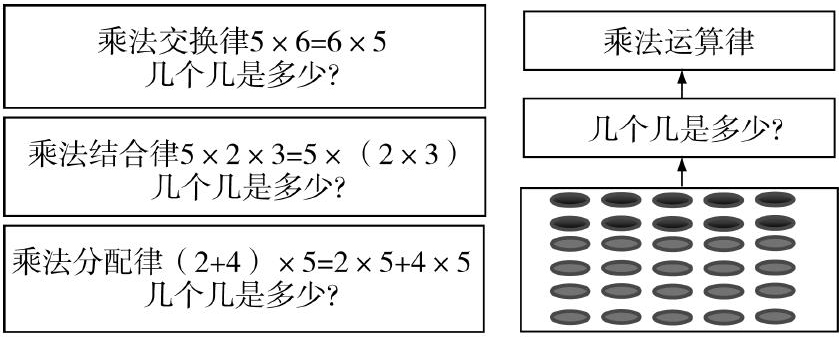
比如在教学乘法的三个运算律时（乘法交换律、乘法结合律、乘法分配律），它们之间有内在联系，其本质都是乘法意义的体现与应用.有人用点子图把这三个运算律进行了整合，以此培养孩子们的发散思维.如下图：

（二）学习方法的迁移与应用，培养学生的逻辑思维

以苏教版五年级上册第二单元“多边形的面积”为例，很多学生都有这样的疑问，为什么我们会背公式，却做不对题目呢？数学有别于其他学科，它注重的是对知识本质的理解，需要自己去经历公式的推导过程，如果是自己推导出来的公式，就算有一天忘记了公式，还可以用以前的方法推导出来.如梯形面积公式推导：

你能想办法求出下面梯形的面积吗？（每个小方格表示1平方厘米）

在用不同的方法动手拼一拼、分一分、摆一摆的活动中，学生可以总结出适合自己的最好的算法.

总之，数学的学习，如果每次都是零散的知识点，则不利于学生的记忆与掌握，也不利于学生发散思维与逻辑思维的培养.如果能思前想后，将知识点的前世、今生以及未来发展都纳入学习考量中，数学学习将变得有根可循，同时可延展出去.

【参考文献】

[1]刘家霞.小学数学课堂有效教学[M].北京：北京师范大学出版社，2015.

[2]皮连生.学与教的心理学[M].上海：华东师范大学出版社，1997.

[3]周卫东.试谈高观点视角下的小学数学教学[J].小学数学参考.2019（3）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。