《体自由度颤振主动抑制的多输入/多输出自抗扰控制律设计》-工学论文，振动工程论文-论文范文参考-科学狗论文网

标题

体自由度颤振主动抑制的多输入/多输出自抗扰控制律设计

范文

沐旭升邹奇彤黄锐胡海岩

摘要：提出了一种新颖的抑制体自由度颤振（BFF，Body Freedom Flutter）的多输入/多输出（MIMO，Multiple In-put/Multiple Output）控制律设计方法。该控制律将受控对象的不确定因素作为“未知扰动”，通过受控对象的输入/输出关系对其进行估计并给予补偿，最后综合出具有高鲁棒性的MIMO输出反馈控制律。为了验证所提出的控制律设计方法对于BFF抑制的有效性，选择一大展弦比飞翼布局无人机为研究对象，分别以机身升降舵与机翼外侧副翼为控制输入，飞机刚体俯仰率和翼尖加速度为反馈信号来设计MIMO自抗扰控制器。对闭环系统根轨迹分布、闭环时域仿真和闭环系统最小奇异值等进行了数值仿真，结果表明该MIMO自抗扰控制律设计方法能有效提高飞机BFF临界速度，可将飞翼布局无人机的BFF颤振临界速度提高约45.3%，并且具有很高的鲁棒性。

关键词：气动弹性力学;颤振主动抑制;飞翼布局飞行器;体自由度颤振;自抗扰控制器

中图分类号：V215.3文献标志码：A 文章编号：1004-4523（2020）05-0910-11

DOI：10.16385/j.cnki.issn.1004-4523.2020.05.006

引言

随着航空工业部门对先进飞行器在气动效率、续航时问以及气动隐身等方面需求的不断提升，研发基于飞翼布局的先进飞行器设计是发展趋势之一。这类飞机一般采用大展弦比机翼设计，以獲得较好的升阻特性，并使用轻质复合材料减轻结构重量，以满足长时问续航任务需求。但由于结构重量轻、柔性大，这类飞机的结构（特别是机翼）在飞行载荷作用下，机翼会产生很大的弯曲变形和扭转变形，结构受载后的气动一结构一控制耦合系统会出现复杂的非线性结构动力学与控制问题，给飞翼布局无人机的设计带来新的挑战。例如，飞翼布局无人机机翼的低阶弯曲振动模态往往会与机体俯仰模态耦合，诱发一种新型的颤振形态——体自由度颤振（BFF，Body Freedom Flutter）。由于刚体模态参与耦合颤振，抑制体自由度颤振现象的发生，除了要考虑刚体模态效应外，还需要考虑对飞行器飞行力学行为的影响，这对颤振抑制技术研究提出了新的挑战。

在传统的飞机设计中，避免颤振的最有效的办法是提高飞机的结构刚度。而提高结构刚度势必会增加飞机的重量、降低飞机的性能，这与现代飞行器追求更轻更快的理念是矛盾的。主动控制技术的发展给解决上述矛盾带来了转机，现代的飞机设计理念发生了如下跨越式发展：在飞机结构设计中，不再以附加结构重量、牺牲飞行性能为代价来提高结构刚度以回避气动弹性问题，而是通过在飞机机翼表面布置多个可操纵的控制面，并设计主动控制系统驱动其联合偏转，提高机翼控制气流的能力，进而主动调节飞行器结构的气动弹性效应。这种主动控制技术在有效抑制颤振的同时也大大迎合了现代飞行器对于高性能的需求。20世纪90年代，美国实施的“主动气动弹性机翼（AAw，Active Aeroelasticwing）计划”首次验证了上述的主动控制设计理念。近年来，关于AFS（Active Flutter Suppres-sion）技术的研究取得了重要进展，有些甚至进行了风洞实验与飞行试验验证。例如，于明礼等采用超声电机作为作动器，研究含控制面的二元翼段的鲁棒颤振主动抑制问题，分别设计了H∞鲁棒控制律和u控制器，并进行了风洞实验验证。黄锐等在南京航空航天大学NH-2亚音速风洞中进行了小展弦比机翼模型的颤振主动控制和闭环颤振模态辨识的实验研究，利用通过极点配置优化设计的线性反馈控制器有效地抑制了颤振失稳，并对机翼模型的在线闭环颤振辨识进行了探索。

上述研究主要是针对机翼模型开展颤振主动抑制技术，少有研究全机模型的颤振主动抑制技术，更为少见的是针对飞翼布局飞行器全机模型AFS技术的研究。杨超等以仿F/A-18A外形的全机模型为对象，采用线性二次型高斯方法，结合平衡截断法降阶，研究了常规布局飞行器模型AFS设计的方法和特点。吴志刚等将基于极点配置的敏感性方法应用到AFS技术中的研究。上述学者的研究虽是以全机模型为研究对象，开展全机颤振主动抑制技术的研究，但并未考虑飞行器刚体模态对颤振主动抑制的影响。Theis等针对明尼苏达大学开发的Mini-MUTT（Multi-Utility Technology Test-bed）模型，用模型的外侧副翼作为控制输入，质心加速度、机身刚体俯仰率与翼尖加速度作为输出反馈，基于鲁棒H∞控制律构造出合理的增广闭环系统并设计控制器，数值仿真结果表明该控制器可有效抑制体自由度颤振失稳并具有较高的鲁棒性。Schmidt针对洛马公司的BFF06模型，利用ILAF（Identically Located Force and Acceleration）方法构造双回路的闭环系统，抑制颤振并增加模型的阻尼，也取得了很好的结果[1引。基于鲁棒控制理论的BFF主动抑制技术虽有所进展，但现有的控制律设计方法鲁棒性有待提高，抗干扰性能存在显著不足。因此，设计具有高鲁棒性、强抗干扰能力、控制律简单并易于执行的体自由度颤振主动抑制系统具有重要的意义。

自抗扰控制理论于上世纪90年代被首次提出后，受到了广泛的关注。该控制理论在结合跟踪微分器（TD，Tracking Differentiator）、非线性状态误差反馈（NLSEF，Nonlinear State ErrorFeedback）以及扩张状态观测器（ESO，Extend-ed State Observer）三大工具后，正式成为一类新的控制技术。该控制技术的核心思想是将作用于被控对象的所有不确定因素都归结为“未知扰动”，而用对象的输人/输出数据对其进行估计并给予补偿。Yang等首次将自抗扰控制理论应用到气动弹性控制律的设计，研究了考虑参数不确定和测量噪声干扰的BACT（Benchmark Active ControlTechnology）机翼的跨音速AFS问题。自抗扰控制技术在飞行器气动弹性控制领域的应用虽取得进展，但仍面临如下困难问题：一是自抗扰控制理论虽然在原理上具备抗干扰和鲁棒性特征，但缺乏鲁棒性判别方法。二是之前的研究均是围绕单输入/单输出控制系统的设计，如何设计多输入/多输出自抗扰颤振抑制控制律也值得研究。三是由于体自由度颤振频率较低、受控系统维数高，导致控制器参数难以整定。

本文的研究目标是对多输入/多输出自抗扰气动弹性控制存在的上述问题进行初步的探索。主要研究内容是以大展弦比飞翼布局无人机全机模型为研究对象，研究全机模型的体自由度颤振主动抑制的自抗扰控制律设计问题。论文的主要框架如下：首先，对所选取的飞翼布局无人机全机模型进行简单介绍，建立考虑刚体自由度的全机气动伺服弹性数学模型并进行体自由度颤振稳定性分析。其次，在自抗扰控制理论的基础上，设计多输入/多输出控制器模型并构造闭环系统。论文的第四部分进行了全机模型仿真，并讨论闭环系统的颤振稳定性与鲁棒性能。论文最后对本文的主要工作和贡献进行了总结。

1飞翼布局飞行器气动伺服弹性建模

飞翼布局飞机具有优异的性能，但同时因其独特的气动布局在低速时就表现出刚体模态与结构弹性模态的耦合，进而引发严重的体自由度颤振。如何抑制飞翼布局飞行器所特有的体自由度颤振失稳是近年来飞行器设计领域的热点与难点。对于体自由度颤振主动抑制精确的动力学建模是气动弹性分析的基础，也是控制律设计的前提。本节将对飞翼布局飞行器模型、多输入/多输出气动伺服弹性建模以及体自由度颤振稳定性分析等进行详细介绍。

1.1飞翼布局飞行器模型

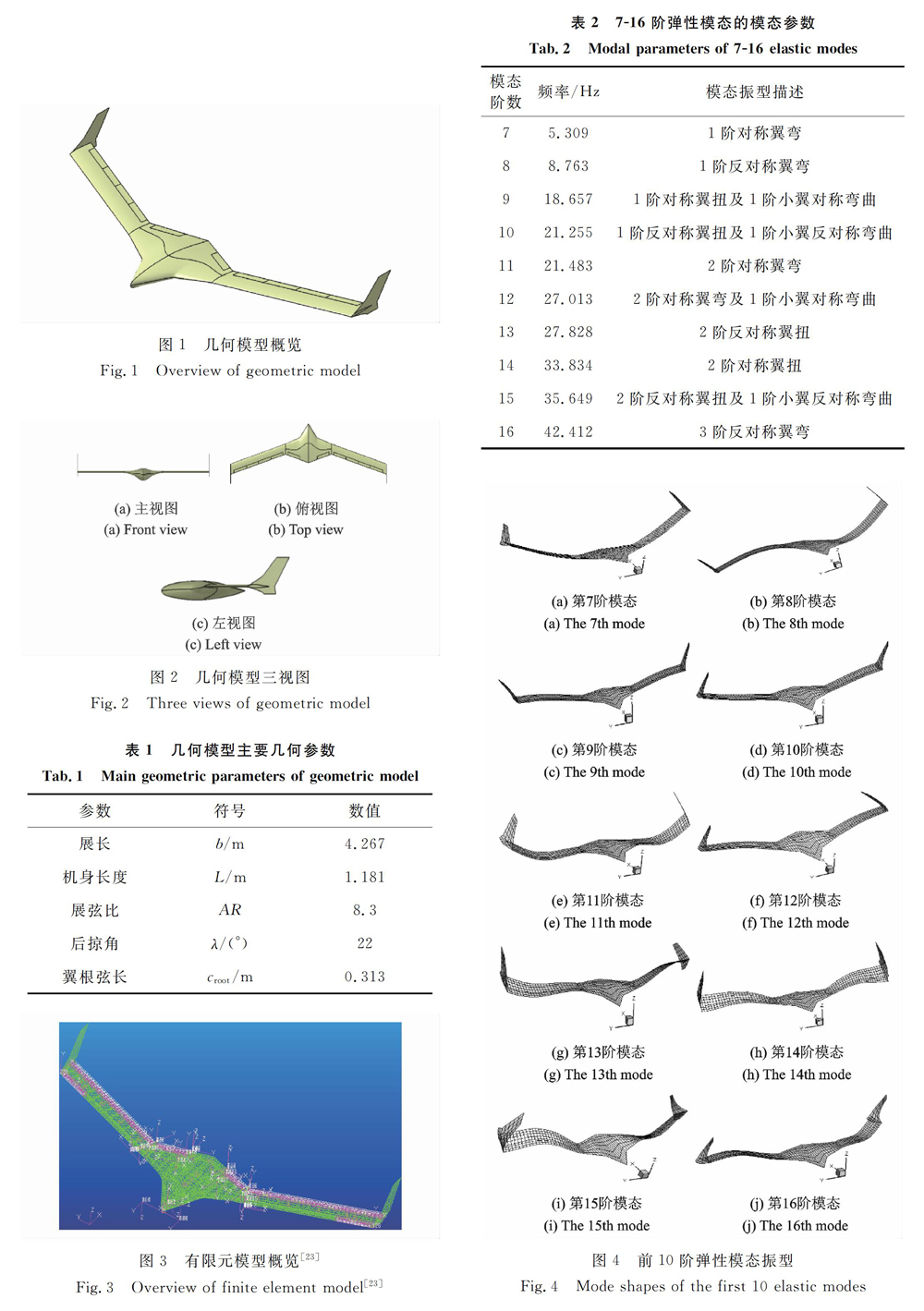
本文研究对象的原始模型是美国明尼苏达大学的MUTT模型与NASA的X-56A模型，作者在这两个模型的基础上建立了几何模型，如图1和2所示，其主要的几何尺寸如表1所示。图3所示为全机有限元模型，通过NASTRAN的自由振动分析模块可容易获得全机的固有模态特征。全机模型的前16阶模态的固有频率和模态振型如表2和图4所示，其中前6阶为刚体模态，7-16阶为弹性模态。

全机模型的控制面配置如图5所示，该全机模型的机翼上有四组舵面（副翼），机身上有一组舵面（升降舵）。在全机模型的气动弹性控制研究中，本文选取了机翼最外侧的一对副翼与机身上的升降舵作为模型的控制输入，机翼翼尖的加速度与机身的刚体俯仰率作为模型的反馈信号。

1.2全机气动伺服弹性建模

气动伺服弹性系统建模的精确性是设计AFS控制律的先决条件。本节将从控制面偏转以及作动器系统建模等方面人手，对涉及ASE建模的各个环节分别进行动力学建模，进而建立一套适用于AFS控制律设计的多输入/多输出ASE数学模型。

借助于分析力学的方法，从系统的功能原理关系出发，利用Lagrange方程，可得到系統运动微分方程。然而对于多数实际飞机结构来说，其结构质量密度分布和弹性模态振型往往无法解析获得，通常只能借助于有限元方法来近似获得。于是，将离散形式的结构的动能和势能代入Lagrange方程中，可以得到如下形式的气动弹性方程

1.3模型颤振分析

当升力面在气流中以一定速度运动时，在弹性力、惯性力和气动力的作用下，刚好使其产生等幅的自激振动，即发生颤振。当飞行速度超过颤振速度后，其振动幅值会随时问不断增加，从而会严重破坏飞行器结构。为抑制飞机的颤振，首先需要求出飞机临界颤振速度。

当获得气动伺服弹性状态方程后，可通过求解状态矩阵特征值的方法来求全机模型的颤振速度。图6（a）所示为开环系统根轨迹随来流风速变化的分布情况。如图所示，当风速接近26.5m/s时刚体俯仰模态穿越虚轴，发生颤振失稳，其颤振频率约为3.6Hz。另外，由根轨迹分布可以看出诱发体自由度颤振失稳的机理是结构第1阶对称弯曲模态与俯仰模态耦合。图6（b）所示为发生体自由度颤振时的颤振形态。

2多输入/多输出自抗扰控制律设计

本节将介绍基于自抗扰控制理论，设计一种不依赖于模型的多输入/多输出自抗扰颤振主动抑制控制律。控制器设计思想是把作用于被控对象的所有不确定因素都归结为“未知扰动”，而用对象的输入一输出数据对它进行估计并给予补偿，能够很好地提高闭环系统的稳定性。本节将分别从自抗扰控制器（ADRC，Active Disturbance R ejection Control-ler）基础理论、控制器设计以及闭环系统构建这三方面分别叙述。

2.1自抗扰控制理论基本原理

2.3闭环控制系统构建

由于飞翼布局飞行器体自由度颤振模态为刚体俯仰模态与第1阶弯曲模态的耦合，本文的控制思路为分别利用机身刚体俯仰率与机翼翼尖加速度作为控制输入，利用机身上的升降舵与机翼最外侧副翼构成反馈对这两个模态分别施加控制。按照这个思路构建如图8所示的闭环控制系统框图。框图共有4个控制器，其中控制左右对称位置舵面的控制器参数相同。

两组控制器的参数分别调节，参考文献[26]中给出的部分线性ADRC调参规律（如式（25）），并通过闭环系统根轨迹分布来指导参数的调节过程。同时，文献[29]证明，咒阶ADRC可以有效地作用于阶数大于n的系统，且高阶的n可能会导致系统噪声的放大，降低控制器的稳定性。在本研究中，作者根据预期的控制器适应性和抗干扰性来决定n的取值。两组参数的调节要使闭环系统的根轨迹尽量与原开环系统的根轨迹类似，也就是说，要保持颤振模态为体自由度颤振中耦合的第5阶或第7阶模态，而其他模态的频率与阻尼变化要尽可能小，这样获得的控制器才能更加可靠且拥有高的鲁棒性。同时可以根据最小奇异值图来分析闭环系统的鲁棒性，最小奇异值大于0.3的闭环系统被认为鲁棒性较好。随着模型飞行速度的增加，闭环系统的最小奇异值会逐渐降低以至于不能抵抗外界的干扰，使控制器起不到其应有的效果。最终整定获得的自抗扰控制器Ka（翼尖加速度回路）与Kp（俯仰率回路）的参数分别为：boa=259403072，ωca=0.01，ωoa=2.0;bop=259403072，ωcp=80，ωop=800。

为方便进行时域仿真与鲁棒性分析，本文将图8中虚线框内的4个并联的控制器综合为1个增广的控制器K_au，其状态空问方程为：

两方程中各符号的含义均已在前文中叙述，在此不再赘述。于是闭环控制系统框图可简化为图9所示形式。

3数值仿真与验证

本节将进行全机模型的闭环气动伺服弹性仿真，以评估控制系统的性能，仿真的过程借助于MATLAB软件完成。本文利用根軌迹分布以及时域响应曲线来评估闭环系统的稳定性，用最小奇异值曲线来评估闭环系统的鲁棒性。同时，这三组曲线也是作者调节参数过程中的依据，当稳定性与鲁棒性达到预期的要求之后，就可以预测在实际的飞翼布局飞行器模型上也能起到良好的效果。

3.1闭环系统稳定性分析

图10所示为开环与闭环系统的根轨迹分布对比图。如图所示，本文所设计的控制器可将颤振速度由开环时的26.5m/s提升到了约53.5m/s，体自由度颤振临界速度提升了约101.89%，此时闭环系统的颤振模态由原来的第5阶俯仰模态变为了第7阶弯曲模态。并且从图中可以看出，控制器对于ASE模型的高阶模态与其他如气动力滞后根、作动器状态变量的影响较小。因此，控制器除了能有效地抑制BFF之外，并不会诱发高频模态失稳。

自抗扰控制器对于全机模型颤振抑制的效果也可以通过图11-14更直观地表现出来。图11，12分别展示了在30m/s时全机模型的翼尖加速度与机身刚体俯仰率的时域响应曲线。在30m/s时，开环系统是不稳定的，从图11，12也可以看出，在微小扰动的作用下，前0.8s模型的翼尖加速度与俯仰率响应发散，0.8s后，模型升降舵与最外侧副翼发生偏转（如图13，14所示），在舵面作用下模型的翼尖加速度与俯仰率响应很快地收敛下来。且从图13和14中可以看出，升降舵与副翼的偏转基本是差动的，这与图6（b）中俯仰模态与弯曲模态的反相是对应的，因此，控制器能够准确地追踪对应模态，并有效地施加控制。

3.2闭环系统鲁棒性分析

本节将分析闭环系统的鲁棒性。由于实际飞行器模型存在建模不确定性与外界诸多扰动，因此闭环系统具有高的鲁棒性是十分必要的，这样控制器才能在模型有大量不确定性的情况下也能有效地抑制全机模型的颤振。单闭环奈奎斯特方法常用来分析系统的稳定性裕度，然而其在一个瞬时只考虑一个回路的幅值或相角。因此其对于MIMO系统的稳定性裕度的分析，传统的单闭环奈奎斯特方法对于本文所建立的MIMO模型并不适用。本文利用闭环系统的最小奇异值的理论来判断闭环系统的稳定性裕度（鲁棒性），最小奇异值方法能够预测各个回路增益和相角同时变化时的稳定性裕度。

闭环系统回差矩阵的最小奇异值随风速变化的曲线如图15所示，从图中可以看出直到约38.5m/s时系统的最小奇异值才掉到0.3以下，即保证足够鲁棒性。因此，可认为自抗扰控制器闭环模型对于真实飞行器模型可将其颤振边界速度提升约45.3%。

4结论

本文针对飞翼布局飞行器体自由度颤振主动抑制问题，设计了多输入/多输出自抗扰控制律，该控制律设计方法具有鲁棒性高、抗干扰能力强、易于执行等优点。为了验证本文提出的控制律设计方法的有效性，论文选取一大展弦比飞翼布局无人机为研究对象，对控制器的控制性能进行了数值仿真，主要结论如下：

1）飞翼布局飞行器俯仰模态易与结构弯曲模态耦合，诱发体自由度颤振。仅采用机翼后缘控制面作为控制输入，其控制效果并不理想。将机身升降舵也作为控制输入，对翼尖加速度和机体俯仰率分别设计回路，可有效提高体自由度颤振抑制效果。

2）从根轨迹与时域响应的效果来看，本文提出的多输人/多输出自抗扰控制器具有优越的体自由度颤振抑制效果，可将颤振速度提升101.89%，且具有很好的鲁棒性能。

3）当考虑飞行器在实际飞行过程中存在的不确定性与外界扰动，在保证足够鲁棒性的前提下，全机模型的颤振速度仍能提高约45.3%，这个结果也达到了作者的预期。

此外，作者计划后期进行一些风洞实验与飞行实验来进一步验证基于线性ADRC的AFS技术。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。