网站首页  词典首页

请输入您要查询的论文：

　

标题 九宫图的教与学
范文 金绍鑫
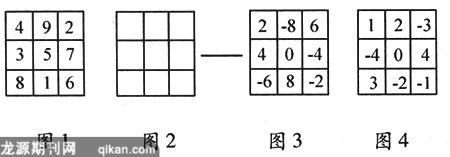
北师大版教科书七年级数学第二章有理数及其运算，多次安排了在3×3的小方格里填数的习题. 其中，把1、2、3…8、9这九个自然数填进小方格，并且使图中各行、列及斜对角的三个数字之和都相等的图形，叫做九宫图(如图1)，这是一个古老的称谓. 古书上记载：“九宫者，二四为肩，六八为足，左三右七，载九履一，五居中央. ”


关于九宫图，北师大版教科书正文并没有作介绍，与之相关的几处习题都安排在“联系拓广”部分，有的题还加了星号，其用意是把它们作为有理数的加减运算的拓展练习. 因此，很多教师对此没有引起足够的重视，常常是一带而过. 我认为，这段内容还有以下几个特点：首先，它有趣，能吸引学生；其次，它有探索性，便于自主探索和合作交流；其三，可突出“转化”这一重要数学思想的教学；其四，有较强的延伸性和研究价值. 教科书的习题安排是有讲究的. 下面，我们来看看教科书的习题安排以及应采取的相应的教学措施.
第二章第4节有理数的加法中习题2.5的“联系拓广”中带星号的题：“将-8，-6，-4，-2，0，2，4，6，8这九个数分别填入图中(笔者注：即图2)的九个空格中，使得每行的三个数，每列的三个数，斜对角的三个数之和均为0”. (结果为图3)老师可视情况采取两种教学方式：若学生基础较好，将上题作为家庭作业，让其自主探索，而后根据作业情况，做相应的指导点评；若学生基础不好，老师可将该题作为例题讲解，讲解时提示学生思考：这九个数的和为多少?每行、列、斜对角的和应各为多少?这九个数有哪些特点?猜想0应填在什么位置?一对相反数应填在什么位置?讲完例后，再将题中九个数改为-4、-3、-2、-1、0、1、2、3、4让学生完成. 有的学生可能很快填出正确结果，有的学生可能填错或未填出，老师要提示学生进行行列调整，然后验算，直至填出正确结果(结果为图4). 最后让同座的同学对照一下，填出的的图形是不是完全一样?有没有不一样的地方?不同形式的两个图形能不能互化，总共有几种形式?为后边的学习埋下伏笔. 这实际上是九宫图教学的初级阶段——感受体验，做好铺垫. 由于此时才学有理数的加法，不便对-8、-6、-4、-2、0、2、4、6、8与-4、-3、-2、-1、0、1、2、3、4进行互化，它们之间的联系要待后继学习之后再建立.
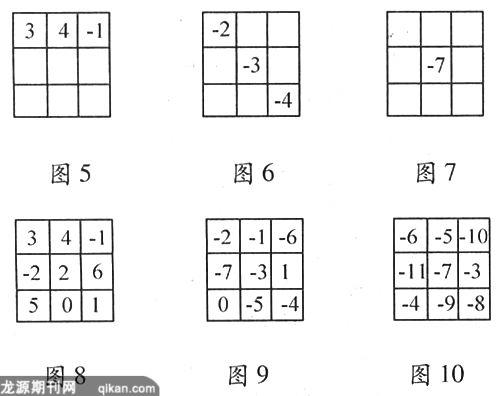
接下来，有理数的减法中的习题2.6“联系拓广”中的两个题：“1.下面是一个方阵图(笔者注：图4)，每行的3个数，每列的3个数，斜对角的3个数之和均相等.如果将方阵图中的每个数都加上同一个数，那么方阵中的每行的3个数，每列的3个数，斜对角的3个数之和仍然均相等，这样就形成了一个新的方阵图. 根据下图(笔者注：即图5、图6、图7)中给出的数，对照原来的方阵图，你能完成下面的方阵图吗? *2.在下图(笔者注：即图2)的9个方格中分别填入1，2，3，4，5，6，7，8，9，使得每行的3个数，每列的3个数，斜对角的3个数之和均相等”. 以后在教科书总复习中还出现过填方阵图的题. 这里的第1题给出图4方阵，让学生按要求将其变为新方阵，老师可先让学生将图4中的每个数都加上1得出一个新方阵，再让他们验算新方阵的行、列、斜对角的3个数是否相等，接着又让学生将图4中的每个数都减去1得出一个新方阵，再让他们验算新方阵的行、列、斜对角的3个数是否相等，作此铺垫后，再引导学生观察：图4第一行与图5第一行发生了什么变化?据此变化图5的第二、三行应填什么数?图4中的1、0、-1分别比图6中的-2、-3、-4大多少?图6的其余小方格应填什么数?图7呢?(第1题结果为图8、图9、图10)完成第1题一是为了培养观察能力，二是为了巩固强化有理数的加减运算，三是为第2题做准备，可谓一题三效，不可小视. 第2题就是填九宫图，题目加了星号，照说比较难，若将它提前到习题2.5中，或孤立地完成第2题，的确比较难，但这里有第1题的方法作铺垫就不太难了. 因为1，2，3，4，5，6，7，8，9每个数都减去5，就得到-4，-3，-2，-1，0，1，2，3，4，而这九个数的填法第1题已经提供，那么再对图4的小方格中的数都加上5，立刻就得到九宫图. 这里“转化思想”起了决定性的作用. 教学时老师一定要让学生观察1，2，3，4，5，6，7，8，9与-4，-3，-2，-1，0，1，2，3，4的联系，让他们自己去悟出九宫图的填法，从而突出转化思想的教学. 第1题的方法还启示我们：不仅图4可以化为九宫图，九宫图也可以施行一定的加减运算，变成它的变式图形，当然这时的图形就不再叫九宫图了. 后面学了有理数的乘除，方阵图的变化更多更方便，上述方阵图之间均可以互化，例如图3与图4之间的互化. 由此看出九宫图的教学对学生学好有理数运算，强化思维训练的确是很有意义的. 学生只要掌握了转化思想方法，不仅对于填出九宫图不会觉得难，而且还会兴趣盎然地深入研究下去，甚至对学习其它数学知识产生积极影响(有条件的班级可将十六宫图、二十五宫图作为研究性学习内容). 这里，老师的教学一是要注意激趣，比如向学生介绍一些九宫图的传说，九宫图自身的八种表现形式等；二是要进行变式教学和沟通前后的联系. 例如，九宫图怎样变为图4?图8、图9、图10能不能变成九宫图?每种图是不是都有八种表现形式?老师还可根据自己班情设计其它类型的题目. 习题完成后，作为反思，老师应向学生指出：上述图形虽可生出很多变化，但万变不离其宗，这里的宗，就是每个图中各行、列及斜对角的三个数字之和都相等. 抓住了这个根本，九宫图可转化为它的变式图，它的变式图(九个数成等差数列)也可转化为九宫图. 最后老师还可让学生回味思考：图4是怎样填出来的呢?填图4时，首先应填那个数，填在什么位置，为什么?它有什么决定性的作用?四个角的数与四边中间小方格的数有何特点，四个角的数能不能分别填入四边中间小方格?又为后边的学习进一步埋下伏笔. 这是九宫图教学的中级阶段——联系比较，变式训练.


到了期末总复习，再做类似于九宫图这样的题目时，应当站得更高一些，从方程角度来研究. 比如，九宫图正中间的小方格为什么要填5，能不能填其它的数?待学了方程组之后，还可从方程组角度研究. 这是九宫图教学的高级阶段——融会贯通，深化认识. 作为复习，教学时首先应启发学生回顾九宫图的填法及其变式图形(图4)的填法，因为它们之间存在等价关系，若忘了九宫图的填法，可以通过先填出图四后再填出九宫图，显然图四的填法更简单更容易掌握. 应当说，前面的学习，使学生对九宫图有了一些了解，但认识是肤浅的，还处于感性认识阶段. 总复习时，再从方程角度来研究，不仅可以深化对九宫图的认识，使之从感性认识上升到理性认识，还可以突出方程思想的教学，渗透推理证明，可谓一举几得. 老师们不要轻易丢失了这一宝贵的教学资源.
下面我们从方程(组)的角度来研究九宫图的填法，供老师们参考.
首先，证明九宫图正中间的小方格只能填5. 设九宫图正中间的小方格的数为x. 因为1，2，3，4，5，6，7，8，9之和为45，所以各行、列、斜对角的三个数之和都等于15.取中间一行的三个数、中间一列的三个数以及两组斜对角的三个数，它们的和是15×4；另一方面，它们的和等于1，2，3，4，5，6，7，8，9之和再加上3x，即有45+3x=15×4，解得x=5. 所以九宫图正中间的小方格只能填5. 再证明偶数只能占四个角. ①一组斜对角的三个数之和为15，而正中间是5，则另两个数不可能一奇一偶；②假如1，5，9在一组斜对角，则3，7就不能在另一组斜对角，否则一行或一列的三个数之和超过15了. 同理2，8或4，6也不能在另一组斜对角，所以1，9不能与5共一组斜对角；③假如3，5，7在一组斜对角，则另一组斜对角只能含4，6，则4与7必在同一行或同一列，该行或列就会重复出现4，与题设矛盾，所以四个角不能都是奇数，也不能一对奇数一对偶数，即四个角全为偶数，显然2，5，8在一组斜对角，4，5，6在另一组斜对角. 那么四个奇数的位置也就唯一确定了. 老师向学生讲解完后，作为巩固练习，可让学生完成对图四的证明，进一步解决前边学习留下的悬念. 或者老师讲图四的证明，学生完成九宫图的证明. 采取哪种方式，完全取决于班上学生情况.
九宫图的教与学是一段难得的好教材. 它对于培养学生热爱数学，热爱生活，勤于思考，勇于探索，并学会如何观察问题，如何发现问题，如何转化分析，如何证明结论，如何总结提炼都有重要作用，老师们应当尽力挖掘教科书的潜在教育功能，既注意眼前的近期目标，又注意未来的长远目标.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 2:29:36