网站首页  词典首页

请输入您要查询的论文：

　

标题 探究2016年高考四川卷函数导数试题的命题方法
范文 杨苍洲+崔红光
面对一个试题，大多数人都喜欢研究试题的解法，而笔者却更喜欢探究试题背后的故事.笔者常思考，命题者是如何得到问题，并将其设计成试题的呢？
试题的解题方法固然很值得研究，但是此类研究往往只停留于对试题较低层次的认识.而探究试题的命题背景、命题方法，不仅有助于在解题中寻找入口、理顺思路、开阔视野，从而提高解题水平，同时也能大幅提高教师的命题水平.下面笔者探究2016年高考四川卷函数与导数试题的命题方法，并根据此命题方法进行试题命制.
1试题与解答
题目（2016年高考四川卷理科）设函数f（x）=ax2-a-lnx，其中a∈R.
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）确定a的所有可能取值，使f（x）>1x-e1-x在区间（1，+∞）内恒成立（e=2.718…为自然对数的底数）.
解析（Ⅰ）由题意，f′（x）=2ax-1x=2ax2-1x，x>0.
①当a≤0时，2ax2-1≤0，f′（x）≤0，f（x）在（0，+∞）上单调递减.
②当a>0时，
f′（x）=2ax+12ax-12ax.
当x∈0，12a时，f′（x）<0；
当x∈12a，+∞时，f′（x）>0.
故f（x）在0，12a上单调递减，在12a，+∞上单调递增.
（Ⅱ）令g（x）=1x-e1-x=ex-1-xxex-1，

令s（x）=ex-1-x，则s′（x）=ex-1-1.
而当x>1时，s′（x）>0，所以s（x）在（1，+∞）内单调递增.又由s（1）=0，有s（x）>0，
从而当x>1时，g（x）>0.
（1）当a≤0，x>1时，f（x）=ax2-a-lnx<0，此时f（x）（2）当a>0且12a≤1时，即a≥12时，令h（x）=f（x）-g（x）B（x≥1），
h′（x）=2ax-1x+1x2-e1-x>x-1x+1x2-1x=x3-2x+1x2>x2-2x+1x2>0.因此h（x）在（1，+∞）内单调递增.又由h（1）=0，从而当x>1时，有h（x）>0，即f（x）>g（x）成立.
（3）当a>0且12a>1时，由（Ⅰ）知f12a0，因此f（x）>g（x）不恒成立.
综上所述，a≥12.
2命题手法探究
上述试题是怎样命制出来的呢？
命题者构造了过定点（1，0）的函数族f（x）=ax2-a-lnx.随着实数a取值范围的变化，函数f（x）的单调性、极值都发生变化.
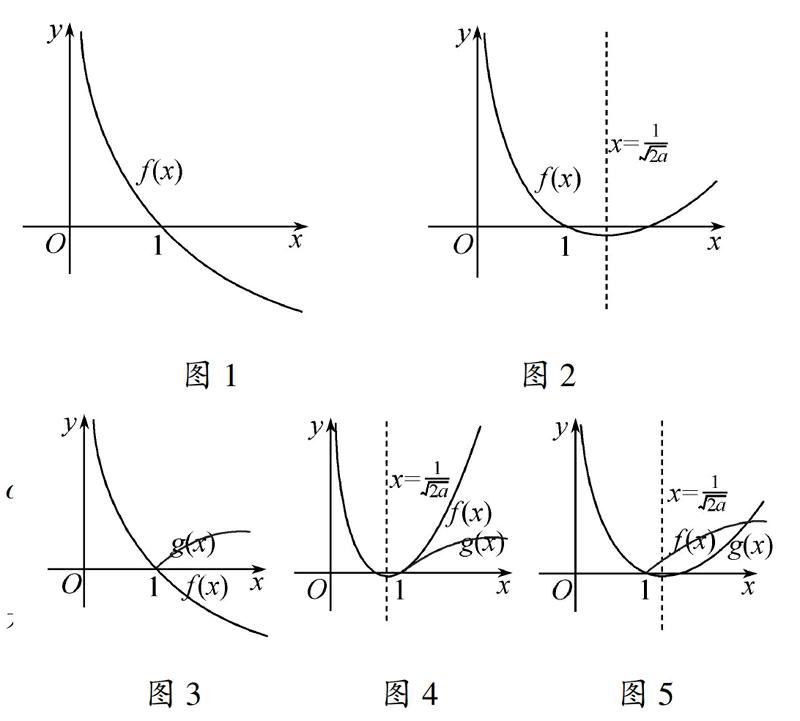
当a≤0时，函数f（x）在区间（0，+∞）单调递减（如图1）；
当a>0时，函数f（x）在区间0，12a上单调递减，在区间12a，+∞上单调递增（如图2）.图1图2于是命题者设置了问题（Ⅰ）：讨论函数f（x）=ax2-a-lnx的单调性.
为了增加试题难度，命题者考虑引入新函数，于是构造了过点（1，0）的函数g（x）=1x-e1-x.
由于动函数f（x）与定函数g（x）相交于点（1，0）.于是考虑比较f（x）与g（x）在定点两侧函数值的大小.为减小试题的难度，命题者只研究两个函数在定点右侧的情况，即研究x>1时，两函数值的大小关系.
如图3，当a≤0时，函数f（x）的图像恒在函数g（x）图像的下方.
图3图4图5如图4，当a>0且12a≤1时，函数f（x）图像恒在函数g（x）图像的上方.
如图5，当a>0且12a>1时，函数f（x），g（x）的图像有异于点（1，0）的又一交点（p，q）.
当1p，函数f（x）的图像在函数g（x）图像的上方.
根据上述分析，命题者设置了问题（Ⅱ）：确定a的所有可能取值，使得f（x）>g（x）在区间（1，+∞）内恒成立.
此类问题的命题手法为：研究过同一定点的两个函数（其中一个为动函数，一个为定函数）的函数图像关系，并从中提炼设置问题.
如能探明试题的命题方法，解题者就不难得到解题思路了.讲题时，也将有利于教师讲清问题的来龙去脉.
3命制新题
基于对2016年高考四川卷理科函数导数试题命题手法的研究.模仿此命题手法，笔者尝试编制新题.
新题1：已知函数f（x）=ex-ax有极值1.
（Ⅰ）求实数a，并确定该极值为极大值还是极小值；
（Ⅱ）当x∈0，+∞）时，f（x）≥mxln（x+1）+1恒成立，求实数m的取值范围.
解（Ⅰ）f′（x）=ex-a.
①当a≤0时，f′（x）>0，f（x）在（-∞，+∞）上单调递增，无极值，不符合题意；
②当a>0时，f′（x）=0，x=lna，当x∈（-∞，lna）时，f′（x）<0，f（x）单调递减；
当x∈（lna，+∞）时，f′（x）>0，f（x）单调递增.
当x=lna时，f（x）取到极小值，f（lna）=a-alna=1，得a=1.
（Ⅱ）f（x）=ex-x.
令g（x）=ex-x-mxln（x+1）-1，x∈[0，+∞），g′（x）=ex-1-mln（x+1）-mxx+1.
构造函数h（x）=ex-1-mln（x+1）-mxx+1，x∈[0，+∞），h′（x）=ex-m1（x+1）2+1x+1，h′（0）=1-2m.
①当m≤0时，h′（x）>0，h（x）在0，+∞）上单调递增，h（x）min=0，则g′（x）>0，g（x）单调递增，g（x）min=0，
所以g（x）≥0，故ex-x≥mxln（x+1）+1恒成立.
②当00，h（x）在0，+∞）上单调递增，h（0）min=0，则g′（x）>0，g（x）单调递增，g（x）min=0，所以g（x）≥0，ex-x≥mxln（x+1）+1恒成立，此时0③当m>12时，h′（x）递增，h′（x）min=1-2m<0，当x→+∞时，ex→+∞，-m1（x+1）2+1x+1→0，h′（x）→+∞，则x0∈（0，+∞），使得h′（x0）=0，当x∈（0，x0）时，h′（x）<0，h（x）递减，此时h（x0）综上所述，k的取值范围是（-∞，12].
新题2：已知函数f（x）=x2-x，g（x）=ex-ax-1.
（Ⅰ）讨论函数g（x）的单调性；
（Ⅱ）当x>0时，f（x）≤g（x）恒成立，求实数a的取值范围.
解（Ⅰ）g′（x）=ex-a.
①当a≤0时，g′（x）>0，g（x）在（-∞，+∞）上单调递增；②当a>0时，当x∈（-∞，lna）时，g′（x）<0，g（x）单调递减，当x∈（lna，+∞）时，g′（x）>0，g（x）单调递增.
作者简介杨苍洲（1979—），男，福建泉州人，中学一级教师，研究方向：数学教学，命题研究.泉州市中小学名师工作室成员，福建省第二届教师教学技能大赛特等奖者.多次参与泉州市质检命题，福建省质检命题，福建省高考命题.在中数期刊发表文章200多篇.
崔红光（1981—），女，福建泉州，中学一级教师，研究方向：数学教学，命题研究.曾获得泉州市说课比赛二等奖，泉州市普通高中高考九科试卷命制技能比赛二等奖.




随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 10:03:10