网站首页  词典首页

请输入您要查询的论文：

　

标题 培养建模意识，提升数学思维能力
范文 沈玉美
[摘 要]数学模型的构建对学生的学习有着很大的促进作用。教师应着重培养学生的建模意识，可从手势、数学符号等入手，逐步渗透，使学生学会运用数学符号表征数学规律，学会将实际问题抽象为数学问题，最终提升数学思维能力。
[关键词]建模意识；手势；抽象化；符号化
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）29-0064-02
在经历两轮大循环教学后，笔者认为学生学不好数学的最根本原因是对概念、算理的理解不够透彻，对数量关系没能建立正确的联系。细究到底，这是教师在教学中没能培养学生的建模意识，没能引导学生建立数学模型所致。《义务教育数学课程标准（2011年版）》明确指出：“数学教学应该从学生已有生活经验出发，让学生亲身经历将实际问题抽象成数学模型并理解运用。”笔者以为，无论在哪个学段，都应该重视对学生数学建模意识的培养，以促进学生分析问题和解决问题的能力的提高。
一、利用手势初步认识建模
张奠宙教授认为：“广义地讲，数学中各种基本概念和基本算法，都可以叫作数学模型。”关于四则运算的概念，小学低年级段的教材中并没有具体阐述，一年级上册关于加法的概念只用一幅图（如图1）一笔带过。

通过观察教材的图画，学生初步了解加法的概念：把两个数合并成一个数的运算，叫作加法。
对于减法的概念，教材同样只是利用一幅图画（如图2）揭示其含义：从一个数中减去另一个数的运算。
实际教学中，学生阅读这些内容后对概念的理解并不深刻，甚至觉得这些内容很乏味。笔者对此进行反思，不断探索既能提高学生学习兴趣，又易于学生理解概念的教学方法。终于，笔者发现利用手势辅助教学，可事半功倍。如教学“加法”时，笔者会做图3所示的手势，边说边做，强调使用加法的标志性动作：合起来。而教学“减法”时，笔者则配上图4所示的手势，由合到分，形象展示减法的本质属性：从总数里去掉一部分。

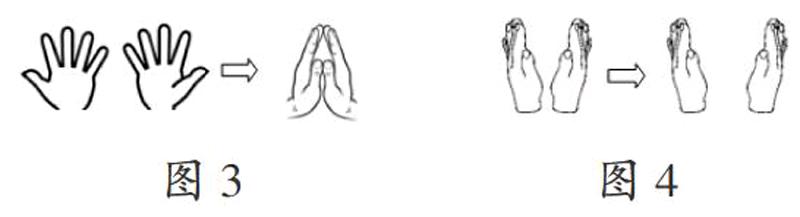
手势对学生在以后的学习中理解加法和减法各部分之间的关系有很大的益处。心理学家认为：“人的大脑左半球指挥着右手，右半球指挥着左手，左右手交替使用，有利于智力的发展。”小学生的注意力不稳定、持续时间短，恰当运用手势这一基本的建模手段，能促进学生理解和内化抽象的数学概念，既能调动学生的学习积极性，又能有效突破概念抽象的难点，为学生的思考提供形象支撑。
二、实际问题抽象化，建构数学模型
《义务教育数学课程标准（2011年版）》明确规定：“要使学生受到把实际问题抽象成数学问题的训练，形成用数学的意识。”在遇到实际问题时许多学生往往茫然不知所措，教师若能引导学生将实际问题抽象为数学问题，构建数学模型，便能使问题迎刃而解。
如：甲、乙两人相距10千米，若他们同时出发，相向而行，甲每小时走3千米，乙每小时走2千米，甲带着一条狗，狗每小时跑5千米，它和甲同时出发，遇到乙时又掉头向甲跑去，遇到甲时又向乙跑去……如此下去，当甲、乙两人相遇时，这条狗一共跑了多少千米？读完题目后，多数学生没有头绪，只有少数学生能先按顺序计算甲和乙相遇前狗从甲的身边跑到乙的身边的路程，狗再从乙的身边跑到甲的身边的路程……然后把狗所跑的路程相加。不可否认，这种方法固然可行，但却很烦琐、笨拙，且不便于计算。教师不妨引导学生将此题所需要解答的实际问题“这条狗一共跑了多少千米？”抽象成数学问题：已知狗的速度，求狗跑的路程。随后，根据“路程=速度×时间”这个数量关系去求甲和乙相遇所需的时间：时间=路程÷速度。显然，狗所跑的时间=甲和乙相遇所需的时间=路程÷（甲的速度+乙的速度）=10÷（2+3）=2（小时）。至此，就得到一个具有一般意义的数学模型，再结合已有的计算公式，不难求出狗一共跑了5×2=10（千米）。
这样教学，学生充分经历“实际问题→抽象→数学问题→数学问题的解→实际问题的解”的转化过程，提高了自身的解题能力和数学思维能力。教学中，教师应有意识地引导学生观察、分析、概括实际问题，然后逐步抽象为数学问题，构建数学模型，最后利用所学知识加以解决，培养学生的建模能力。
三、强化符号意识，助学生构建数学模型
数学的显著特点是符号化，因此，在教学中强化符号意识有利于提高学生构建数学模型的能力。
如“认识5以内的数”第一课，教材编排了一幅“教师节快乐”的主题图（主题图从左到右依次展示实物图、算珠图、数字）。通过这样的一一对应关系，学生认识到1～5中的每个数字都是有意义的符号，这些数字和算珠一样，表示的是物体数量的多少。数字比算珠抽象，但使用起来却更为方便，适用范围也更广。练习时，笔者要求学生思考：“1还可以表示什么？2、3、4、5呢？”有学生说：“它们可以表示年龄，比如1岁、2岁、3岁、4岁、5岁。”有的学生说：“可以表示时间，比如1小时、2小时、3小时、4小时、5小时。”这种训练从具体、形象的实例开始，借助操作予以内化和强化，最后通过思维发散和联想加以扩展和推广，赋予数字以更多的“模型”意义，增强了学生的建模意识，丰富了学生对数的认知。
此外，笔者还常结合教学内容开展能激发学生进行联想的活动，提高他们驾驭数学符号的能力。
如教学“列竖式计算三位数加减三位数”的三组对比题时，笔者让学生先计算第一组算式，然后观察这组算式中的三个算式。
236+152= 327+89= 538+387=
388-236= 416-327= 925-538=
388-152= 416-89= 925-387=
学生发现后面两个算式是第一个算式的逆运算，即“和-加数=另一个加数”。在此基础上，笔者增加一个问题：如果用“a+b=c”表示第一个算式，那么第二个和第三个算式应该怎样表示？学生略作思考，很快给出答案：c-a=b，c-b=a。
字母是数学符号中的一种，用字母表示规律是数学中的常用方法，也是数学规律的一般呈现形式，体现了数学的简约美。
在小學阶段渗透数学建模思想不仅可以激发学生学习数学的兴趣，增强学生探索数学的好奇心，还有助于学生理解和掌握数学知识与技能，发展学生的数学思维。作为数学教师，应当根据教学内容和学生的年龄特点组织教学，循序渐进，在各个学段都要进行数学建模思想的渗透，切实提高学生的数学思维能力。
（责编 吴美玲）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 21:55:51