网站首页  词典首页

标题	基于NARX神经网络的港口集装箱吞吐量预测
范文	范莹莹+++余思勤 摘要：为对港口集装箱吞吐量进行科学预测，采用带外生变量的非线性自回归（NARX）模型对上海港的集装箱吞吐量进行预测，通过主成分分析法对港口吞吐量影响因子进行相关性分析，将筛选出的GDP作为外部输入因子引入NARX模型，实证分析发现，引入GDP的NARX神经网络模型对具有非线性特征的集装箱吞吐量数据有良好的映射逼近性，训练后的网络误差小且拟合度高，具有良好的泛化能力，预测性能较好. 关键词：NARX神经网络；集装箱吞吐量；主成分分析；动态预测 中图分类号：U691.71；TP183 文献标志码：A 0 引言 集装箱运输的发展已成为政府、企业和学术界甚为关注的一个问题.在上海，贸易和物流业占地区生产总值的比例很高，而集装箱运输是国际贸易和物流业的主要运输方式，上海港集装箱吞吐量连续5年位居世界第一.但是，近年来，随着国际经贸的发展，上海港与周边港口之间的竞争日趋激烈，上海港集装箱运输面临很多问题.本文采用带外生变量的非线性自回归（NARX）模型，建立上海港集装箱吞吐量预测模型，并进行实证分析，为上海港未来发展规划提供决策参考. 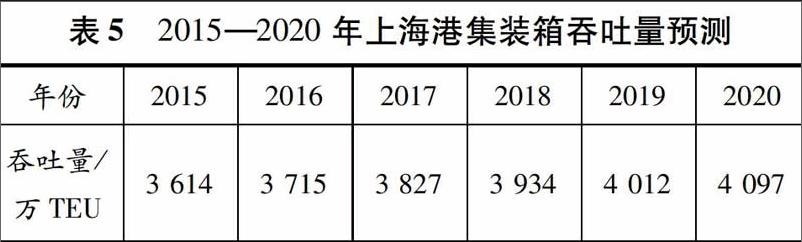关于港口集装箱吞吐量的研究始于20世纪80年代，目前预测方法主要有时间序列法、回归分析法和因果关系法.如：施泽军等和崔巍等运用灰色模型和指数平滑法对宁波港集装箱吞吐量进行预测；徐杏等和林强等以吞吐量作为单变量构建神经网络，在深度挖掘历年数据的内部规律后对深圳港集装箱吞吐量进行预测；朱小檬等和王文采用组合分析法建立自变量与因变量的关系模型对国内港口集装箱中长期吞吐量进行预测.集装箱吞吐量变化具有复杂性和动态性，上述方法存在一定的局限性，预测精度不高，都不能完全描述吞吐量非线性时间序列的特征.结合时间序列法和因果关系法，本文采用主成分分析法筛选出集装箱吞吐量的重要影响因子GDP，将其作为外部输入引入NARX动态神经网络模型，对2015-2020年上海港集装箱吞吐量进行预测，为港口未来的发展及定位提供参考. 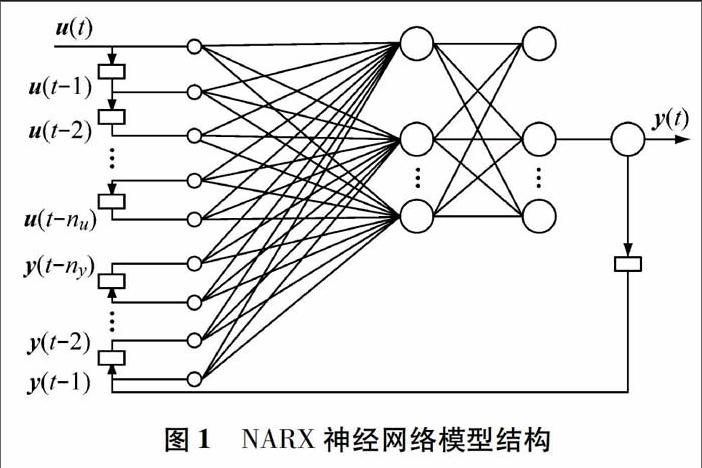1 模型选择及分析 神经网络模型是反映大脑系统及功能的抽象数学模型，具有能够通过训练逼近任意非线性映射的特点.相对于无输出反馈的静态神经网络模型，NARX神经网络模型通过引入延时模块及输出反馈建立模型的动态递归网络，它将输出向量延时反馈引入网络训练中，形成新的输入向量，图1给出NARX神经网络模型的结构，u（t）表示输入向量，y（t）表示训练时的目标向量.在训练、验证及测试过程中，网络模型的输入不仅包括原始输入数据，还包含经过训练后的输出数据，网络的泛化能力得到提高. NARX神经网络模型的数学模型可表示为 y（k）=f（y（k-1），y（k-2），…，y（k-ny）， u（k-l），u（k-2），…，u（k-nu），w） （1）式中：u（·）为输入向量u（t）在某时间点的数值；y（·.）为目标向量y（t）在某时间点的数值；nu（nu≥1）为非线性系统的输入阶数，ny（ny≥1）为输出阶数，且nu≥ny；w为网络的权重矩阵；f是训练过程中形成的非线性函数. 港口集装箱吞吐量系统具有高噪声、非平稳和非线性时间序列特征.针对吞吐量数据的特征，在选择预测模型时，应考虑过去输入与输出对当前输出的影响，因此本文选择建立NARX神经网络模型对上海港集装箱吞吐量进行预测. 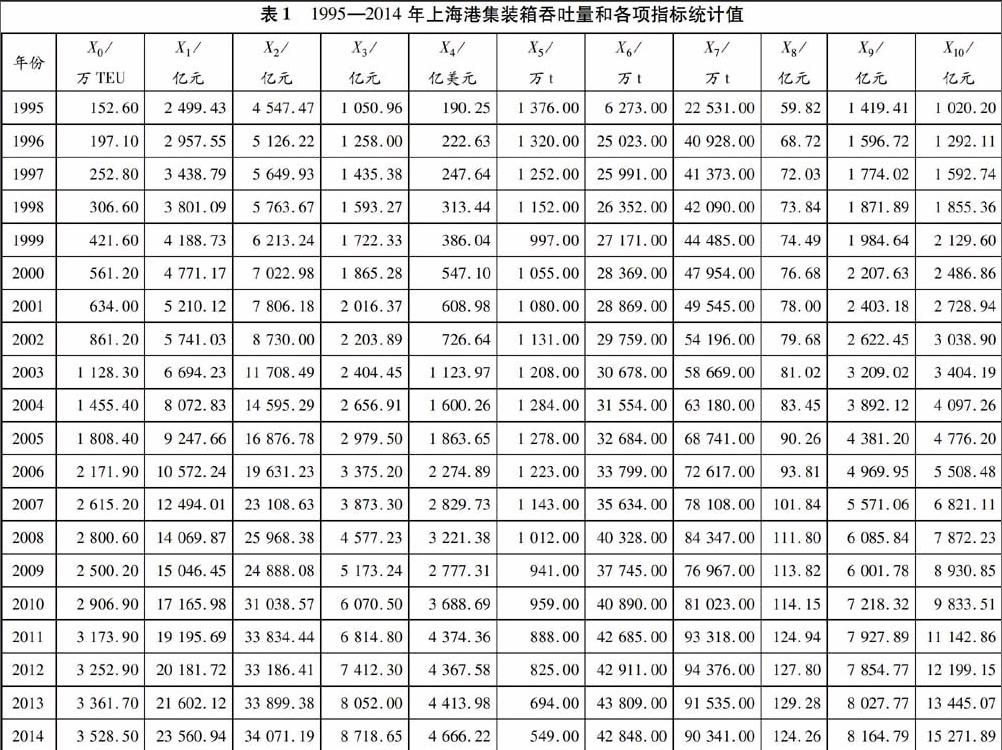2 外部输入因子的选择 外部输入因子的选择是NARX神经网络模型模拟过程中重要的一部分，其选择恰当与否直接关系到模型预测的适用性和精确度，这里借鉴国内外学者的实证研究成果，并结合上海市的实际情况，认为区域经济发展水平和交通行业政策是影响上海港集装箱吞吐量的决定因素.选取GDP（X1）、工业生产总值（X2）、社会消费品零售总额（X3）、外贸进出口额（X4）、铁路货运量（X5）、公路货运量（X6）、总货运量（X7）、第一产业产值（X8）、第二产业产值（X9）、第三产业产值（X10）等10项指标作为港口集装箱吞吐量（X0）的影响因子.表1给出1995-2014年上海港集装箱吞吐量和各项指标的统计值. 为消除影响因子的量纲差异，运用MATLAB的zscore函数对原始数据进行标准化处理.对各项指标进行相关性检验，结果见表2.各影响因子之间的相关性系数绝对值均接近1，说明各影因子之间存在高度的相关性，为消除影响因子之间的相关性，运用软件对标准化后的数据进行主成分分析，一般认为只有特征值大于1的指标才具有有效性；方差贡献率反映因子相对影响的大小，累计方差贡献率大于85%才能基本反映原始数据的信息.在表3的指标主成分分析结果中，只有GDP的特征值大于1，且累计方差贡献率达到93.28%，基本包含所有指标的信息，因此本文选取该变量作为预测模型的外部输入因子. 3 模型构建及检验 NARX神经网络模型是将y（t-l），y（t-2），…，y（t-ny），u（t），u（t-l），u（t-2），…，u（t-nu）作为输入，y（t）作为输出的一种基于BP算法的分类行为，这里选取1995-2014年上海市GDP数据作为x（t）形成网络的输入，港口集装箱吞吐量数据作为y（t）形成网络的输出，建立如图2a所示的NARX神经网络模型，
随便看	高中音乐课堂教学有效性的策略探析 基于核心素养的初中数学高效课堂的构建研究 初中语文文言文高效教学策略探析 对初中英语课堂教学互动有效性策略的探究 新课改下初中语文高效课堂的实践与研究 找准课堂兴奋点 打造魅力英语课堂 高中数学教学中问题导学法的应用思考 走出舒适区，挑战不可能 物理课堂理论探究型研究性教学的实践分析 初中数学“问题串”教学的策略分析 基于核心素养视角下初中生数学解题能力的培养研究 探究初中数学教学中归纳推理意识的渗透 巧用创意戏剧元素 助燃幼儿园体育教学活动 历史地图在初中历史与社会教学中的应用分析 基于数学核心素养的初中三角形教学策略研究 新媒体背景下小学语文课堂的趣味性教学探讨 基于“互联网+”背景下中职数学教学模式探析 “互联网+”环境下初中信息技术教学内容的优化策略 归纳初中语文多媒体有效整合的途径 探究高中信息技术教学的开展策略 浅析高中生物教学中多媒体课件的应用 初中数学作业布置与批改的差异化分析 数据分析在高中生物教学评价中的应用 论高中物理习题教学中学生思维能力的培养 浅谈中职班主任管理策略与技巧 ejection ejections ejects eke eked eked-out eke-out eke out eke out a living/an existence ekes ekes-out eke sth out eke sth ↔ out eking eking-out elaborate elaborated elaborately elaborateness elaboratenesses elaborates elaborate² elaborate¹ elaborating elaboration 烦虑 烦襟 烦言 烦言碎语 烦言碎辞 烦请 烦躁 烦躁不安，心事重重 烦躁忧愁 烦躁恼怒 烦躁恼怒的样子 烦躁愤怒 烦躁愤懑 烦躁易怒 烦躁生气 烦躁疲劳 烦躁的心情 烦躁的样子 烦躁着急 烦躁缠绕 烦躁，气恼 烦躁，烦闷 烦透了 烦速 烦郁

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。