网站首页  词典首页

标题	例谈如何建构“乘法分配律”的概念
范文	代婷 [摘 要]对于“乘法分配律”，学生能熟记公式，但却会滥用或误用。通过强化乘法分配律的现实意义，让学生经历乘法分配律的抽象过程，能使学生真正明白乘法分配律的含义，从而正确运用。 [关键词]乘法分配律；简算；记忆；逻辑；表象；构建；抽象；过渡 [中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）02-0041-01 对于乘法分配律，学生背得滚瓜烂熟，但在具体套用的时候，时常因为不能够领悟其中的要领而屡屡犯错。受简算思维的负迁移影响，学生在做题时往往为了凑整而枉顾客观事实和数学原理，生硬地将毫无联系的两个数结合起来，造成一种形式上的乘法分配律。如何才能解决学生会说不会用的窘境呢？ 一、强化意义，语词逻辑记忆 乘法分配律不仅有助于简算，它还有着广泛的实际应用。当感知到乘法分配律在生产活动中带来的便利，学生自然就会产生强烈的学习动机。因此，教师不妨以一些生活实例作为导入。如： （1） 一套校服，上衣45元，裙子38元，买3套这样的校服需要多少钱？ （2） 给厨房贴瓷砖，左面墙壁每排贴6块，贴9排；右面墙壁每排贴4块，贴9排。一共需要多少块瓷砖？ 熟悉的生活情景，消除了新知的疏离感。但成功的教学不仅要揭露乘法分配律的现实意义，还应揭露其数学意义。教师也可以通过绘图让学生在具体、形象的情境下对乘法分配律形成第一印象和整体感知。对于第二个问题，一位男生提出了“（a+b）×c”和“a×c+b×c”这两种近似长方形面积计算的方法，这就是乘法分配律的原型了。学生能够从生活实例的数字形式联想到字母取代的符号形式，形象思维跃升到抽象逻辑思维水平。在教师还没有正式介绍分配律之前，学生已经能创造出分配律的雏形，这也是思维概括性和间接性的集中体现。思维的这两个特性互相作用，互相促进，以前感知到的表象材料都可以在学生头脑中集中闪现、交织联系，然后产生新的认知。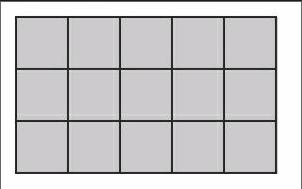 二、不断抽象，去粗取精 用长方形周长来配给形象思维下的乘法分配律的表象材料，有一定的局限性，教师还可以添加“动”的元素，利用课件画一个长方形（如下图），让学生从长方形的面积去思考乘法分配律。教师也可以先把“贴瓷砖”转化为画格子图，进一步抽象乘法分配律。 首先，教师利用课件一行一行地显示灰色小正方形，数出数量，得出算式5×3。 其次，教师出示算式4×3，让学生思考该如何画出方格图，然后一行行显示无色小长方形，并接在上图的后面。 再次，教师提问：“现在一共有多少个小正方形？”然后引导学生列出综合算式5×3+4×3和（5+4）×3。 最后，去掉格子线，突显“（a+b）×c=a×c+b×c”的另一层含义：长方形面积图。如此顺势而为，逐步从“小正方形的数量”过渡到“纯数字”，再抽象为“字母符号”，用乘法运算的性质来诠释乘法分配律。 三、牢記特征，瞬时构建 语词逻辑记忆虽然不受环境因素的干扰，但一旦其中的某一个片段出现模糊，就会影响整个记忆系统。所以，教学时要设置一些辨识度高、特征鲜明的情境，让学生只要看到乘法分配律或意识到要用乘法分配律，脑海中就会不自觉地闪现这些情境，从而在情境的回忆中正确运用乘法分配律。例如，一位教师用打比喻的方式帮助学生记忆乘法分配律的公式：c性格开朗，交友广泛，一开始先结识了a，后来又认识了b，最后c拉着它们结拜。又如，c妈妈肚子里怀有一对双胞胎，一个是a，一个是b，a和b两个先一起待在妈妈肚子（括号）里，后来a和b钻出来，一人一边拉起妈妈的手。两人在妈妈肚子里是兄弟，出生后在妈妈的连接下还是一对兄弟。 比喻虽然不是很贴切，但胜在新颖、有趣，能在学生的脑海中留下深刻印象。心理学研究表明，如果在陈述一个概念时列举一些幽默的范例，可以帮助学生进行更精确的复述。以幽默的语词解说知识，尤其是一些深奥抽象的概念，可以使其通俗浅显，降低难度，提高效率。 综上所述，针对“乘法分配律”的教学实践，执教者不能裹足于让学生采用不完全归纳法推理出分配律的现状，还应该注重记忆表征形式的转型升级，从图形到数字再到字母符号，让学生全面地掌握乘法分配律的意义。 （责编 吴美玲）
随便看	热胁迫对不结球白菜生理指标的影响 中国罗非鱼产业安全预警分析 创新创业人才需求背景下现代农业培育的路径探析 基于高质量发展视角的农机购置补贴政策完善 基于全产业链视角的鲜活农产品流通体系创新研究 核桃仁脱皮机设计 石佛寺水库二维水动力数值模拟 基于窄带物联网的中药材种植智能测控系统设计 基于本体的农村信息化服务平台用户模型 农业科研院所国际合作信息化管理系统的设计与实现 基于改进杂草算法的温室农场多载AGV调度研究 基于GBS测序开发SNP在植物上的应用进展 基于低酸法优化核桃油脱胶工艺参数 不同冻藏温度对鳜鱼鱼肉品质变化的影响 商洛蕨菜总黄酮体外抗氧化活性研究 不同干燥处理对荷叶离褶伞品质的影响 电感耦合等离子体质谱法测定水产品中17种重金属 不同保鲜液对切花牡丹观赏品质和生理的影响 猪粪中添加不同比例牛粪对蚯蚓养殖的影响 miR-6523a对延边黄牛垂体细胞中生长激素分泌的影响 转地饲养方式对西方蜜蜂形态特征的影响 西方蜜蜂群势与气候的周年变化及相关性分析 基于组合赋权的甘薯品种抗病性模糊综合评价 烟草—玉米轮作对烟草病毒病的影响 贵州剑河钩藤主要病虫害种类及综合防治 middle ground middle-income middleincome middleman middlemanagement middle management middle manager middlemanship middlemarket middle market middlemen middle name middle names middleness middle of the night middle-of-the-road middle of the road middle-of-the-roader middle-of-the-roaders middle of the roadism middle-of-the-roadism middle-of-the-roadisms middle-of-the-roads middle-ranking middleranking 六国古文 六国血于秦 六国贩骆驼 六境 六声 六够 六大师 六天 六头君 六头子 六奇 六好工人 六如居士 六妍 六姻 六子 六字真言 六安茶 六宗 六官 六宫 六宫清穆 六宫粉黛 六宫都太监 六害

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。