《基于改进凝聚算法与铁路网的社团划分》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于改进凝聚算法与铁路网的社团划分

范文

李勤敏郭进利

摘要：為了更好地分析铁路网划分过程及其与周边经济发展状况的联系，以省为单位建立加权无向复杂网络，其中节点为省，两省之间的铁路连线为网络连边。提出改进的凝聚算法，进一步对网络社团划分的迭代过程展开分析，最后得出明显的南北社团划分分界线。将社团划分过程与经济发展情况相联系，分析得出铁路发达情况与区域间经济发展息息相关，从而得出结论：铁路间联系越紧密，区域经济带动作用越强，并证实了国家近年来大力发展铁路建设的重要性。

关键词：改进Newman快速算法;社团划分;铁路网

DOI：10. 11907/rjdk. 181573

中图分类号：TP319文献标识码：A文章编号：1672-7800（2019）001-0132-04

Abstract：In order to analyse the process of community identifity and the relation of community identifity and economic development， we create weighted network through taking Privoce as node and the railway between Privoces as weighted edge. An improved Newman fast algorithm is used to analyse the process of iteration and we can get a clear divide between south and north in the graph.Contacting the process of community identifity and economic development，we get the conclusion that they are interrelated with each other and railway development drives the development of economy and area.In this way，we can find the importance of national support of the development of railway construction.

0 引言

在对复杂网络的研究中，由于大部分网络都是加权复杂网络，有必要对复杂网络的拓扑性质及社团划分等方面更多地引入加权情况。复杂网络的社团性质能够更好地将社团根据相互间的联系程度与相似程度对整个网络节点进行分类。通过社团的划分，社团内部节点之间的联系紧密程度比社团之间的联系紧密程度更高，即各个社团之间的联系更加稀疏。

早前对复杂网络的研究主要集中在无权网络图上，如Kernighan-Lin算法是1970年Lin & Kernighan[1]提出的基于试探性优化的贪婪算法，通过多次交换不同社区节点计算网络模块度Q，不断搜寻可使Q增大的社团划分方式，利用贪婪算法找出最大Q，从而得到最佳社团划分方法。该算法的缺陷是每次只能将网络分成两个大小已知的社团;GN算法是一种最常见的分裂算法，于2002年由Girvan & Newman提出，其基本步骤为：①找出网络所有边的介数;②移除网络中具有最高介数的边;③重复上一步，直到每单个节点都分别退化成一个社团为止。该算法具有较高精度，但其复杂度也很高。与分裂算法相对应的是凝聚算法，凝聚算法包括Newman快速算法、利用堆结构的CNM算法与结合谱分析的贪婪算法，其简化了算法复杂度，使社团划分方法能够更好地运用于当今的Internet等复杂大数据网络。

近年对加权网络的研究也越来越多，对于加权复杂网络社团划分研究进展如下：2008年宣照国等[2]对Newman快速凝聚算法作加权改造，根据两节点的相似程度将节点与社团进行合并;2010年韩华等[3]提出对CNM算法进行加权算法改进，将CNM算法中的[eij]与[ai]引入边权、点权概念，拓展了CNM的应用范围;2013年鹿静等[4]提出基于加权网络的节点相似度划分算法，构造节点相似度矩阵，将相似度大的优先合并;2013年王秀凤等[5]以社交关系网络为例研究并设计了加权关系网络算法;2016年Xiaoming Liu[6]等对节点的随机游走进行研究，得出边缘更加紧密的连通子图具有较大权重，周围节点更容易聚合为一个社团结构，但对大型网络进行社团划分的方法未考虑节点连边权重对游走的影响;2016年Fang Hu等[7]结合PageRank算法与CNM算法，基于节点重要性对社团划分算法进行改进，增加了算法的可靠性，但未考虑网络连边是加权网络的情况;2017年DONG MIN等[8]提出k-权关系矩阵，k为无圈情况下i与j之间存在节点的个数，同时考虑了加权情况的k，基于加权模块度矩阵设计迭代算法，使其应用于大型加权网络的社团划分。

本文通过对Newman快速算法进行简单改进，将网络节点之间的连边权重引入算法中，使社团划分算法更易于理解，且接近实际情况。与此同时，本文应用改进的Nenman快速算法对通过三横五纵简化的各省之间铁路主干线复杂网络图进行社团划分，并结合实际情况展开分析，并将划分过程与经济发展结合起来。

1 简单铁路网络构造

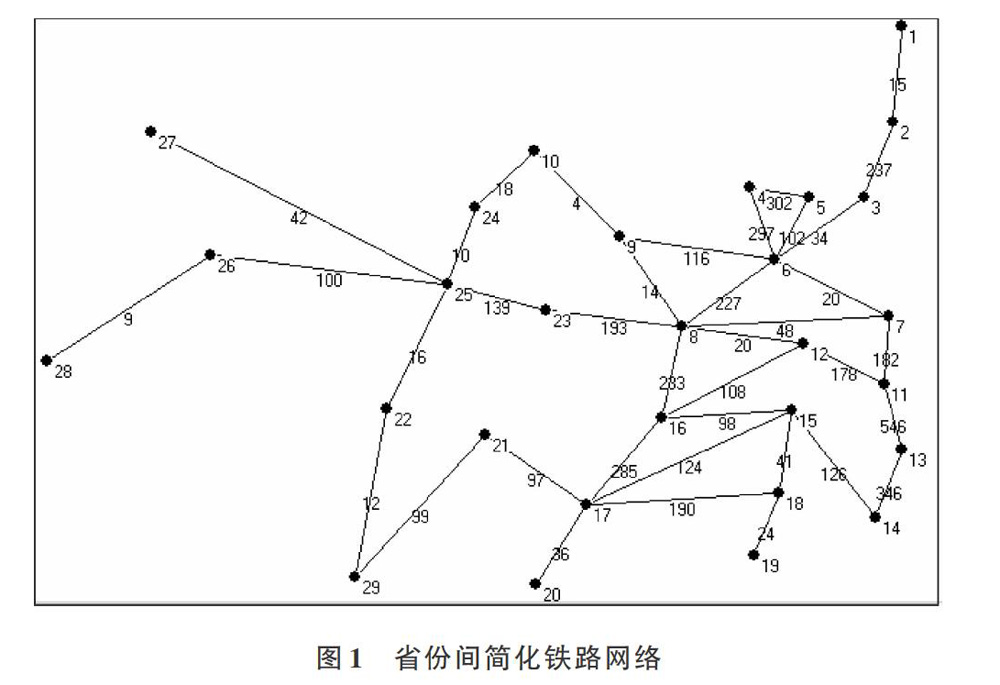
结合三横五纵所经过的省构造简化铁路网络的加权无向网络，首先将铁路经过的省份作为网络图的节点V，若在简化的铁路网上两省之间存在铁路连线，则可看作两省之间存在连边E。为方便计算，取各省的省会城市作为计算点，将两省会之间每天往返两地列车的总班次数量记为两省节点连边权重[9]，每天的往返列车班次可通过12306官网进行查询，然后作出统计并取平均。对各省代表的节点进行标号，如4-北京、5-天津、6-河北，对三横五纵铁路主干线网经过的省份进行网络图绘制，并且通过Pajek[10]画出对应网络，如图1所示（数据统计时间为2017年12月，忽略时间因素导致的不精确情况）。

Pajek绘制结果显示图中参与省份一共有29个节点、69条连边，整个网络的平均度为2.62。

2 改进的凝聚算法

Newman快速算法是由Newman在GN算法基础上提出的另一种快速凝聚算法，算法主要基于贪婪算法思想，从一开始即将单个节点看成一个社团，假设合并社团并求出各个模块增量，根据模块度增加最大的方向对社团进行合并，并不断更新网络的社团模块度，从而得到最大模块度的步骤。这里将复杂网络社团节点之间连边的权重引入算法中，以期更加准确地划分社团，并且降低社团划分算法的复杂度。

对于网络图G（V，E）（表示具有V个节点、E条连边的网络图）的网络社团划分算法过程，其中[eij]是指社团i与社团j之间连边权重占整个网络边数总权重和的比例，[ai]为一端与社团i中节点相连边的权重占网络总权重的比例，W指整个网络所有边的权重之和，[ωij]指社团i与社团j之间连边的权重和[11]。算法具体步骤描述如下：

（1）初始化：一开始将每个节点分别看成互相独立的社团，初始模块度值记为[Q=0]，[eij]、[ai]计算方法如式（1）、式（2）所示，其中[ωij]即為节点i与j之间连边的权重。

（2）按照顺序依次对有边相连的社团进行合并，计算合并后的模块度增量，再根据贪婪算法原理，社团朝着模块度增加速度最快的方向合并，[ΔQ]迭代公式如下：

3 算法结果

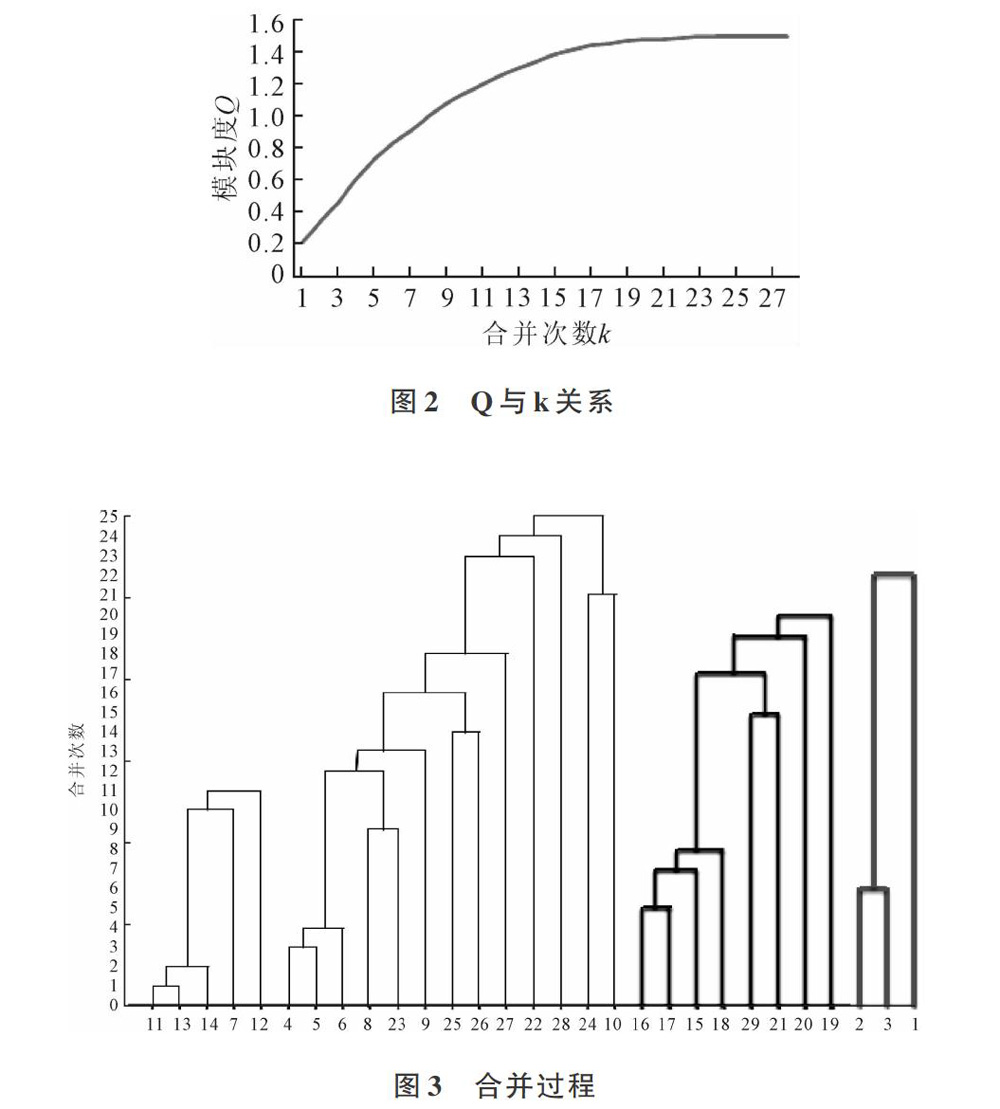
3.1 合并次数与Q关系分析

3.2 迭代步骤分析

迭代第1步，mdq=0.214 5（这里mdq为贪婪算法中挑选的最大值）。合并点11（江苏）与点13（上海）为n+k=30，将合并后的点重新标号为30;第2步，mdq=0.128 3，合并点30（江苏上海）与点14（浙江）为n+k=31，将合并后的点重新标号为31;依次继续迭代，到第13次迭代，mdq=0.046 7，合并点41（河北，北京，天津，陕西，河南）与9（山西）为n+k=42。此时即社团合并前13次迭代，得到如图4、图5所示结果。

按照优先选择[？Q]最大的贪婪算法合并原则，将网络分成东西两部分，因为联系紧密的优先合并，所以相较于西边，东边省份之间联系更为紧密。由于铁路的发达程度可以对各省市之间的经济发展起到一定带动作用[14]，城市之间铁路的连接有利于提升可达性，与区域经济成正比关系。社团网络划分过程形成了东西分界线，与实际相符合。合并到第25次时，mdq=0.002 0，合并节点53与节点50，n+k=54，Q=1.498 7，此时网络的模块度Q达到最大值，得到4个社团，结果如图6所示。

在上一步分析以后，社团的划分情况开始跨越南北，最终社团呈现如图6所示的节点54、51、40、49。铁路网络联系的紧密程度能够影响并且带动周边城市发展[15]，将社团合并的先后顺序与经济发展相结合，得出推论：对于节点51（黑龙江，吉林，哈尔滨），跨省经济主要由节点2（吉林）-3（辽宁）带动，根据2016年东北三省的GDP排名，辽宁省居第一;节点40经济带（上海、江苏、浙江、山东、安徽）中，11-13-14（江苏、上海、浙江）为联系最紧密的部分，显然上海、江苏带动了该经济带连线之间的经济发展;与节点49（西南一部分省）联系最紧密的是首先合并的社团16（湖北）-17（湖南），两省经济产生的联合效应带动了区域发展;对于节点54（以北京、天津、河北为首的中国北部及西北部分），其中北京、天津、河北的连接发挥了主要作用。这符合区域经济发展中，小部分城市带动整个区域发展的情况，称为经济作用的火车头[16]。由此可见，社团划分过程通常以一个hub点为基础，成为周边联系的纽带。

4 结语

将铁路网连边权重引入Newman快速算法，对该算法进行简单改进，引入节点之间的权重，从而使算法作用的社团划分更加符合实际情况。本文通过对k-Q图像进行分析，再结合贪婪算法思想对算法过程进行剖析，发现在基于三横五纵的铁路网中，我国的东边铁路之间联系更加紧密，而西边相对稀疏，根据贪婪算法的加权Newman快速算法，先合并的是东边省份。我国经济东西分界线也是铁路主干线的东西分界线。网络最后分为4个社团，各个社团内部又由联系相对紧密的经济带所带动。对原有的Newman快速算法进行改进，根据改进算法对铁路发展与对应地区经济进行分析，分析结果符合我国铁路连线发展情况以及对经济带动作用的实际情况，可明显看出铁路网东西发展不平衡的现状。基于铁路与经济的紧密联系，我国为进一步发展铁路建设，与此同时带动国家经济发展，国务院常务会议于2016年6月29通过了《中长期铁路网规划》，提出了打造高速铁路“八横八纵”的主干线。本文对社团划分过程进行了分析，以期用复杂网络理论证明铁路网络与经济发展各方面息息相关，最后建议以核心经济带为中心，进一步优化高速铁路网络布局，实现高铁站与城市交通的无缝对接，促进不同地区的经济交流，打造经济一体化环境[17]。

参考文献：

[1] 汪小帆，李翔，陈关荣. 复杂网络理论及其应用[M]. 北京：清华大学出版社，2006.

[2] 宣照国，苗静，党延忠，等. 科研领域关联网络的社团结构分析[J].? 上海理工大学学报，2008，30（3）：249-252.

[3] 韩华，王娟，王慧. 改进的CNM算法对加权网络社团结构的划分[J]. 计算机工程与应用，2010，46（35）：86-89.

[4] 鹿静，徐勇，安丽平. 基于节点相似度的加权网络社团结构划分算法[J]. 信息与控制，2012，41（4）：504-508.

[5] 王秀凤，马英红. 基于加权网络模块强度的社团划分[J].? 计算机应用研究，2013，30（3）：695-698.

[6] LIU X，ZHOU Y，HU C， et al. Miracle：a multiple independent random walks community parallel detection algorithm for big graphs[J].? Journal of Network & Computer Applications，2016，70：89-101.

[7] HU F， LIU Y. A new algorithm CNM-centrality of detecting communities based on node centrality[J]. Physica A：Statistical Mechanics & Its Applications，2016， 446：138-151.

[8] MIN D， YU K， LI H J. Refinement of the community detection performance by weighted relationship coupling[J]. Pramana-Journal of Physics，2017.

[9] 张兰霞，秦勇，王莉. 高速铁路加权复杂网络特性分析[J]. 铁道科学与工程学报，2016，13（2）：201-209.

[10] 李光正，翟龙余，左传桂. 基于Matlab的小世界网络仿真[J]. 科技信息：科学教研，2008（17）：71-72.

[11] 汪小帆，李翔，陈关荣. 网络科学导论[M]. 北京：高等教育出版社，2012：37-38.

[12] NEWMAN M E. Fast algorithm for detecting community structure in networks[J]. Phys Rev E Stat Nonlin Soft Matter Phys，2004，69：066133.

[13] 司守奎，孙玺菁.? 复杂网络算法与应用[M]. 北京：国防工业出版社，2015.

[14] 刘莉文，张明. 高速铁路对中国城市可达性和区域经济的影响[J]. 国际城市规划，2017，32（4）：76-81，89.

[15] 张安民. 浅谈高速铁路建设对我国区域经济的带动作用[J]. 企业技术开发，2014，33（23）：126-127.

[16] 蔡之兵，满舰远. 中国超大城市带动区域经济增长的效应研究[J]. 上海经济研究，2016（11）：3-11，128.

[17] 陈薇薇. 高速铁路建设对我国贸易经济一体化的影响及对策研究[J]. 价格月刊，2016（1）：65-68.

[18] 解，汪小帆. 复杂网络中的社团结构分析算法研究综述[J]. 复杂系统与复杂性科学，2005（3）：1-12.

[19] 杨泽俊，何柳. 复杂网络社区结构发现算法概述[J]. 数字技术与应用，2013（3）：145.

[20] 王天成，劉真真，李天明，等. 复杂网络社团结构划分方法及其应用[J]. 信息通信，2015（8）：43-45.

（责任编辑：黄健）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。