《基于改进遗传算法的柔性作业车间调度研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于改进遗传算法的柔性作业车间调度研究

范文

代招李郝林

摘要：针对中小型企业生产车间柔性作业调度问题，采用改进的遗传算法求解最优调度结果。将最大完工时间最小化作为调度目标，对经典遗传算法进行相应的改进。首先利用粒子群算法获取工序序列与粒子参数之间的映射关系，在初始种群中利用混沌映射和反向学习策略以提高初始种群质量;然后提出一种将机器编码和工序编码相结合的分段编码方法，以解决某道工序有多台可选机器加工的问题;最后利用自适应交叉和变异概率提高算法收敛速度。通过对Brandimarte设计的10组不同规格的基准案例进行仿真实验，得到进化曲线和最优调度方案。实验结果验证了该方法的实用性和有效性。

关键词：遗传算法;作业车间调度;柔性;完工时间

DOI：10. 11907/rjdk.192572 开放科学（资源服务）标识码（OSID）：

中图分类号：TP301文献标识码：A 文章编号：1672-7800（2020）005-0083-05

0 引言

柔性作业调度问题（Flexible Job Shop Scheduling Problem，FJSP）作为生产管理和组合优化问题的重点研究对象 [1]，是传统作业车间调度问题（Job-shop Scheduling Problem， JSP）的扩展，也被划分为强NP-hard问题[2]。FJSP的含义是：工件的工序不但能够在各个机器上进行处理，而且加工耗时也因机器而异，这要求为工件的每道工序分派最适合的机器，同时也要保证工件加工工艺的合理性[3]。所以FJSP更符合车间实际生产环境，是目前亟待解决的调度难题[4]。该问题一般有两个难点：①如何将可选机器集中分派给指定工序;②如何安排工序在机器上的加工顺序。

为解决这类问题，学者提出了遗传算法[5]、蚁群算法[6]、模拟退火算法[7]、粒子群算法[8]等智能优化方法。现有研究结果表明，利用遗传算法求解FJSP效果很好且有独特优势[9-10]。遗传算法求解FJSP时，初始种群质量对最终求解结果和迭代速度有较大影响。目前，用遗传算法求解FJSP时一般采用随机生成初始种群方式，这样在迭代初期会形成许多非法解，只有经过大量的复杂运算后才可能出现较优解，因而导致算法收敛速度低。Kacem等[11]提出了根据加工时间表进行分配的方法，Zhang等[12]提出了依据机器时间数组的分配方法，虽然这两种方法取得了一定效果，但都是基于单步优化策略分配机器的方式，并不能保证最终整体分配质量。

为加快算法的收敛速度，提高机器分配质量，本文试图采用改进的遗传算法解决柔性作业调度问题，改进之处包括：利用粒子群算法得到粒子参数与工序序列的映射关系，在初始种群中采用混沌映射[13]和反向学习[14]策略，选取适应度值前50%作为初始种群，进而提高种群质量，同时不失去其多样性，利用自适应交叉和变异概率提高算法的搜索效率，提高算法的收敛性能。提出将机器编码和工序编码相结合的分段编码方法解决机器分配问题，利用粒子群算法得到优化的初始机器链，对机器分配序号，朝着加工耗时最短的目标方向变异以提高机器分配质量。最后利用不同规格的基准案例进行仿真实验，实验结果验证了本改进算法的实用性和有效性。

1 FJSP调度模型

1.1 FJSP问题描述

通常将柔性作业调度描述为：某生产车间有[m]台机器，[n]个工艺流程明确的工件，每个工件至少有一道工序需在这些机器上加工，每个工序能够在不同机器上进行加工且耗时因机器而异。所以FJSP就是要在满足一定约束条件的前提下，为工件的每道工序分派最适合的加工机器，同时还应对工件工序的加工顺序进行合理编排，以达到最优的性能指标 [3]。FJSP一般由以下几个要素组成：

（1）待加工工件集合。[J=J1，J2，？，Jn]是一个待加工工件数为[n]的集合，每个工件[Ji]都有其加工工艺，[Oij]表示工件[i]的第[j]道工序，在零时刻，所有的工件都能被加工。

（2）加工机器集合。[M=M1，M2，？，Mm]是一个机器数量为[m]的集合。每台设备在同一时间只能对一个工件进行加工且工序一旦开始就不能中断。在零时刻，所有机器都是可用的。

（3）柔性。某道工序能够在可选机器集合中的任一机器进行加工。

（4）约束。主要约束包括：在同一时刻，任何工件的任一工序只能被一台设备处理;每道工序一旦开始处理就不允许暂停;工件之间没有严格的优先级;任一工件的后道工序只有等前道工序加工完成后才能进行。

（5）目标。本文把最大完工时间的最小值作为最优解。即把[n]个工件安排在[m]台设备上加工，使所有加工任务的最大完工时间[Cmax]最小。

1.2 FJSP问题数学模型

本文用一个二维数组proMacArray[][]表示各个工序的可选加工设备及该工序在此设备上的加工耗时，proMacArray[][]中的每个一维数组对应一道工序，一维数组的个数等于所有工件的工序数量之和。任意工件的任一工序可用加工机器用一个一维数组描述，机器编号为该一维数组的索引;该机器加工该工序的耗时为该索引对应的一维数组中的元素值。如表1所示，以工件1的第2道工序（[O12]）为例，其可用加工设备的编号为2和4，对应的加工时间为5和3。

2 改进的遗传算法求解FJSP

2.1 编码与解码

本文采用分段编码技巧，即把染色体分为两部分：①机器选择部分（MS）为染色体的前半部分，由工件工序的可选加工设备编号组成，用来为工序提供加工机器;②工序选择部分（OS）为染色体的后半部分，由工件的各个工序编号组成，用于编排各工序的处理次序。两段长度分别为N，N为所有工件的工序總数。MS和OS通过间接编码方法实现，如图1所示。若[i]为工件编号，则该工件的第几道工序就是[i]在OS段出现的次数值。第一个工件的第一道工序一直到最后一个工件的末道工序所选机器编号，就是MS段中从左至右依次出现的数字。采用这种方式，MS和OS一一对应。

解码可视为编码的逆流程，具体步骤为：首先对OS段进行从左至右的依次遍历，那么工件和工序编号就可据此确定，再根据MS中的值确定加工机器号和加工时间。

2.2 适应度函数设计

车间作业调度顺序是按OS段的编码从左向右依次执行的。当OS编码段中工序加工完成，那么就得到完成调度任务的最大完工时间。我们的目标是最大完工时间最小化，因此适应度值与最大完工时间成反比，计算方法如下：

2.3 初始化种群

经典的粒子群算法是由[n]个粒子组成的一个[D]维搜索空间。每次迭代时，第[i]个粒子会凭借此时整体最优值和历次最优值实行种群间的相互交流，从而更新自身速度和位置，进而使整体种群不停地朝着全局最优解方向靠拢[15]，粒子更新公式为：

2.4 选择

为尽可能让适应度高的个体被保留，本文选择后代个体的方式是以轮盘赌策略为基础，辅以精英策略相结合。轮盘赌策略可有效防止问题的解步入局部最优化陷阱，精英策略则确保种群向更高质量的方向进化，两者有效结合，加速了种群的迭代和求解速度。

2.5 交叉与变异

按照编码方式本文选择算子如下：针对MS利用随机交叉和单点变异算子，针对OS采用顺序交叉、单点交叉相结合的方法和逆转变异算子，下面作简单介绍。

2.5.1 交叉算子

针对MS段采用的是随机交叉算子，其实现流程为：随机将两条染色体中MS部分中的某个局部区间的所有基因进行交换，其交叉过程如图2所示。

OS的交叉过程为：在两亲代染色体[P1]和[P2]中，任意选其中一个基因的位置[i]，然后把[1～i]这一范围内的基因段当成交叉区间，且用[A]和[B]标记交叉区间中的基因段;在[P1]中，把[B]中所有基因值按從左至右的次序进行遍历，然后将[P1]中出现相对应位置的基因去掉，同理操作[P2];然后把[P1]、[P2]中余下的基因位置保持相对位置不变向右移;最后把[P1]交叉区间的基因更换为[B]的基因，把[P2]交叉区间的基因更换为[A]的基因，其交叉过程如图3所示。

2.5.2 变异算子

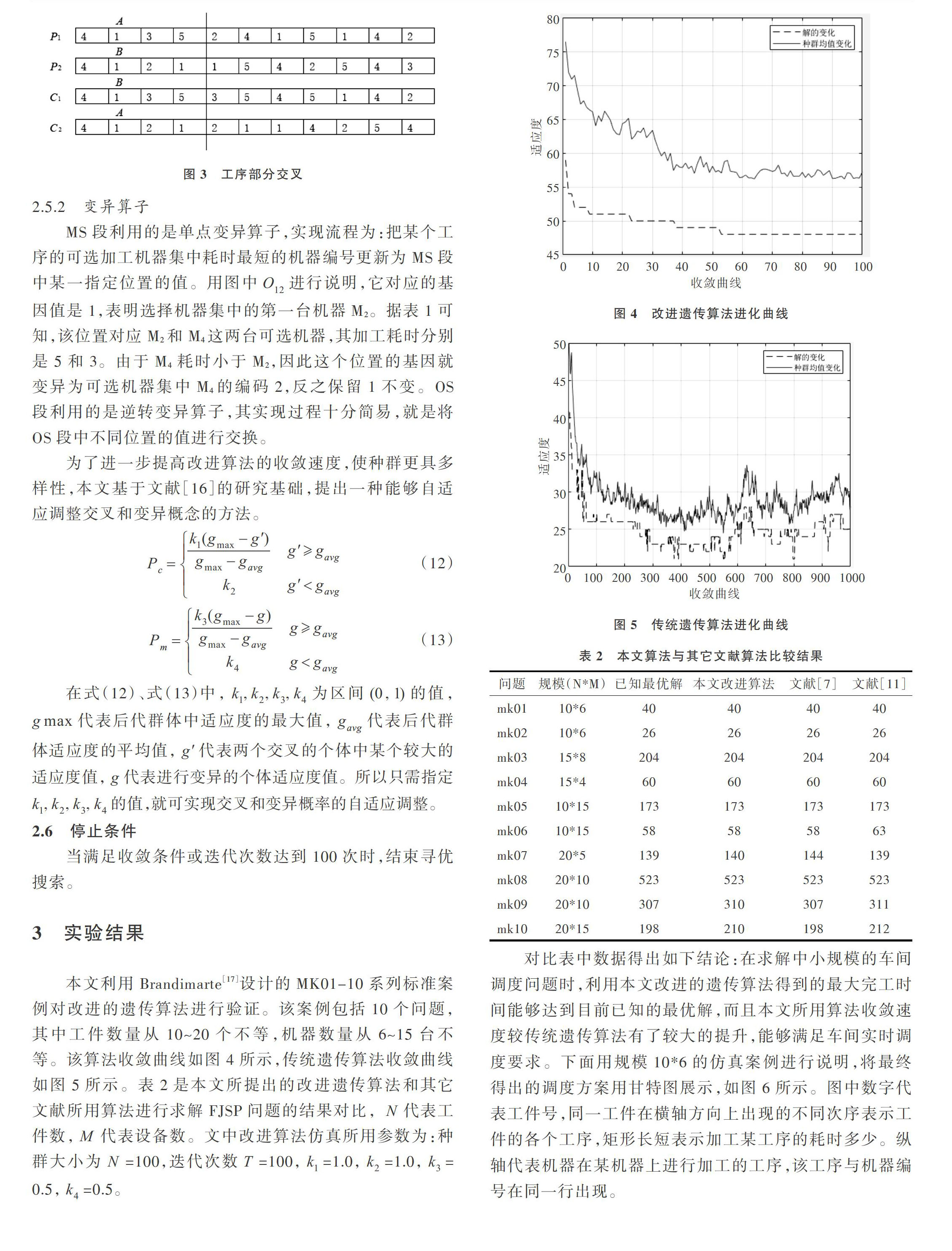
MS段利用的是单点变异算子，实现流程为：把某个工序的可选加工机器集中耗时最短的机器编号更新为MS段中某一指定位置的值。用图中[O12]进行说明，它对应的基因值是1，表明选择机器集中的第一台机器M2。据表1可知，该位置对应M2和M4这两台可选机器，其加工耗时分别是5和3。由于M4 耗时小于M2，因此这个位置的基因就变异为可选机器集中M4的编码2，反之保留1不变。OS段利用的是逆转变异算子，其实现过程十分简易，就是将OS段中不同位置的值进行交换。

2.6 停止条件

当满足收敛条件或迭代次数达到100次时，结束寻优搜索。

3 实验结果

本文利用Brandimarte[17]设计的MK01-10系列标准案例对改进的遗传算法进行验证。该案例包括10个问题，其中工件数量从10～20个不等，机器数量从6～15台不等。该算法收敛曲线如图4所示，传统遗传算法收敛曲线如图5所示。表2是本文所提出的改进遗传算法和其它文献所用算法进行求解FJSP问题的结果对比， [N]代表工件数，[M]代表设备数。文中改进算法仿真所用参数为：种群大小为[N]=100，迭代次数[T]=100，[k1]=1.0，[k2]=1.0，[k3]=0.5，[k4]=0.5。

对比表中数据得出如下结论：在求解中小规模的车间调度问题时，利用本文改进的遗传算法得到的最大完工时间能够达到目前已知的最优解，而且本文所用算法收敛速度较传统遗传算法有了较大的提升，能够满足车间实时调度要求。下面用规模10*6的仿真案例进行说明，将最终得出的调度方案用甘特图展示，如图6所示。图中数字代表工件号，同一工件在横轴方向上出现的不同次序表示工件的各个工序，矩形长短表示加工某工序的耗时多少。纵轴代表机器在某机器上进行加工的工序，该工序与机器编号在同一行出现。

4 结语

为解决中小型企业柔性作业车间调度问题，本文建立了相对应的数学模型，对遗传算法进行改进，以寻求作业调度的最优解。通过改变初始种群的生产方式，利用自适应交叉和变异概率等改进措施，大幅提高了算法的收敛速度和求解质量，能够满足车间实时调度要求。通过一系列标准的实验案例，验证本文改进遗传算法求解FJSP的正确性和有效性。未来将对基于事件的多目标动态调度进行研究。

参考文献：

[1] 徐本柱，费晓露，章兴玲. 柔性作业车间批量划分与并行调度优化[J]. 计算机集成制造系统， 2016， 22（8）： 1953-1964.

[2] 张腾飞，马跃，李力，等. 柔性作业车间调度问题的改进遗传算法[J]. 小型微型计算机系统， 2017， 38（1）： 129-132.

[3] 王明. 基于改进遗传算法的作业车间调度问题研究[D]. 芜湖：安徽工程大学，2019.

[4] ZHANG R， SONG S， WU C. A two-stage hybrid particle swarm optimization algorithm for the stochastic job shop scheduling problem[J]. Information & Control， 2012， 27（3）： 393-406.

[5] BHOSALE KC， PAWAR PJ. Material flow optimization of flexible manufacturing system using real coded genetic algorithm （RCGA）[J]. Materials Today Proceedings， 2018， 5（2）： 7160-7167.

[6] 乔东平，裴杰，肖艳秋，等. 蚁群算法及其应用综述[J]. 软件导刊， 2017， 16（12）： 217-221.

[7] CRUZCHAVEZ M A， MARTINEZRANGEL M G， CRUZROSALES M H. Accelerated simulated annealing algorithm applied to the flexible job shop scheduling problem[J]. International Transactions in operational Research， 2017， 24（5）： 1119-1137.

[8] HUANG S，TIAN N，WANG Y，et al. Multi-objective flexible job-shop scheduling problem using modified discrete particle swarm optimization[J]. SpringerPlus， 2016， 5（1）： 1432.

[9] 王春，张明，纪志成，等. 基于遗传算法的多目标动态柔性作业车间调度[J]. 系统仿真学报，2017， 29（8）： 1647-1657.

[10] 劉胜，于海强. 基于改进遗传算法的多目标FJSP问题研究[J]. 控制工程， 2016， 23（6）： 816-822.

[11] KACEM I， HAMMADI S， BORNE P. Approach by localization and multi-objective evolutionary optimization for flexible job-shop scheduling problems[J]. IEEE Transactions on Systems， Man and Cybernetics， Part C： Applications and Reviews， 2002， 32（1）： 1-13.

[12] ZHANG G H， GAO L， SHI Y. An effective genetic algorithm for the flexible job-shop scheduling problem[J]. Expert Systems with Applications， 2011， 38（4）： 3563-3573.

[13] MAY B R. Simple mathematical models with very complicated dynamics[J]. Nature， 1976， 261（5560）： 459-467.

[14] WANG H， WU Z， RAHNAMAYAN S， et al. Enhancing particle swarm optimization using generalized opposition-based learning[J]. Information Sciences， 2011， 181（20）： 4699-4714.

[15] GHASEMI M ， AGHAEI J ， HADIPOUR M . New self-organizing hierarchical PSO with jumping time-varying acceleration coefficients[J]. Electronics Letters， 2017， 53（20）：1360-1362.

[16] 何斌，张接信，张富强. 一种求解作业车间调度问题的改进遗传算法[J]. 制造业自动化， 2018， 40（8）， 113-117

[17] BRANDIMARTE P. Routing and scheduling in a flexible job shop by tabu search [J]. Annals of Operations Research， 1993（22）： 158-183.

（责任编辑：杜能钢）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。