《基于CEEMD和小波包变换的重力数据信噪分离方法》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于CEEMD和小波包变换的重力数据信噪分离方法

范文

喻伟+赵立业

摘要：为了有效地进行海洋重力测量数据的信噪分离，本文提出了基于互补总体经验模式分解（CEEMD）和小波包变换（WPT）的重力数据信噪分离方法。该方法利用CEEMD将海洋重力测量信号分解为从高频到低频的不同固有模式函数（IMF）分量以及趋势项，为进一步提取出各IMF分量中的有用重力信号，本文采用小波包变换对各IMF分量进行小波包分解降噪，最后将从各分量提取出的有用信号与趋势项进行信号重构，实现重力数据的信噪分离。本文通过仿真数据和实测数据对该方法进行了验证，结果表明本文提出的重力数据信噪分离方法能有效的抑制噪声干扰，保留有用的重力信号，实现较高精度的重力信号提取。

关键词：重力数据；信噪分离；互补总体经验模式分解；小波包变换

中图分类号：TH761 文献标识码：A DOI：10.3969/j.issn.1003-6970.2015.02.011

0 引言

水下运载体由于其工作环境的特殊性，大多以惯性导航作为主要的导航手段。而惯性导航的导航误差会随着时间积累，难以保证长时间的导航精度。重力/惯性组合导航正是利用测量地球重力信息，并以此来修正惯性导航系统的误差，已经成为近年来惯性组合导航领域研究的热点和前沿。因此，研究海洋重力数据处理技术，对于提高惯性导航系统的精度有着重要的意义。

常用于重力测量数据信噪分离的算法有传统的FIR和IIR低通滤波、基于系统模型的卡尔曼滤波和H∞滤波算法以及基于矩阵理论的奇异值分解滤波等等。这些方法虽都取得了较好的滤波效果，但都存在些许不足，如在进行传统的FIR和IIR低通滤波设计时，不同的截止频率和滤波器阶数对滤波效果都有不同程度的影响，卡尔曼滤波和Hoo滤波算法实现的基础是较为精确的系统模型和测量噪声模型，而重力测量的环境复杂多变，动态测量条件下的测量信号信噪比更低，系统模型和测量噪声模型更难确定，两种算法的精度有待进一步验证；而奇异值分解滤波算法需要进行复杂的矩阵运算，计算量较大，滤波效率较低。所以在总结现有研究成果的基础上，我们需要提出更有效的重力测量信号的信噪分离方法。

本文提出了将互补总体经验模式分解（CEEMD）用于海洋重力数据处理的方法。CEEMD是基于经验模态分解（EMD）和总体经验模式分解（EEMD）提出的一种改进算法，是一种自适应的信号处理方法，它可以将海洋重力测量信号分解为从高频到低频的不同固有模式函数（IMF）分量以及趋势项。同时，为进一步提取出各IMF分量中的有用重力信号，本文将CEEMD与小波包变换进行结合，利用小波包变换对各IMF分量进行小波包分解降噪，提取出高频分量中的有用重力信号，最后将从各分量提取出的有用信号与趋势项进行信号重构，实现重力数据的信噪分离，抑制噪声干扰，保留有用的重力信号。

1 基于CEEMD和小波包变换的信噪分离方法

1.1 CEEMD算法理论

CEEMD是基于经验模态分解（EMD）和总体经验模式分解（EEMD）提出的一种改进算法。EMD算法由美国国家宇航局的Huang等人于1998年提出，该算法把任意一个复杂的时间序列分解为有限个固有模式函数（IMF）之和，每一阶IMF都反映原始信号的动态特性。IMF分量必须满足两个条件：a）其极点数和零点数相同或最多相差一个；b）其上下包络线关于时间轴局部对称。EMD方法分解的基本原理是通过不断剔除信号的极小值和极大值连接的上下包络线的均值，具体的EMD步骤为：

3层小波包分解示意图如图1所示，其中X为原始信号，H和G分别为正交共轭低通滤波器和高通滤波器。

1.3 基于CEEMD和小波包变换的信噪分离方法

利用上述的CEEMD算法将重力测量信号进行分解，可以得到从高频到低频的不同固有模式函数（IMF）分量以及趋势项。但是，为了进一步提取出各IMF分量中的有用重力信号，本文提出将CEEMD与小波包变换进行结合，利用小波包变换对各IMF分量进行小波包分解降噪，提取出高频分量中的有用重力信号，最后将从各分量提取出的有用信号与趋势项进行信号重构，实现重力数据的信噪分离。

利用小波包变换进行信号分解时，它可以有效的对高频信息部分继续进行再分解，对各IMF分量作小波包变换，对各小波包系数进行阈值操作以及重构，这样可以有效提取出含在高频分量中的有用重力信号。在对各节点系数进行阈值去噪时，主要有硬阈值和软阈值两种方式，硬阈值去噪可以使噪声几乎完全得到抑制，并且可以保留信号的特征尖点和峰值点，而软阈值去噪法可实现最优估计，保证去噪后的重建信号与源信号有同样的平滑，并且不会产生附加震荡。文中采用基于软阈值的小波包变换的方法对各IMF分量信号进行去噪，软阈值函数表达式为：

综合上述，本文提出的基于CEEMD和小波包变换的信噪分离方法的处理步骤如下：

（1）将采集到的重力数据信号进行CEEMD分解，得到从高频到低频的各IMF分量以及趋势项；

（2）对各IMF分量利用小波包变换进行阈值去噪提取有用信号，本文采用DB4小波基；

（3）将步骤（2）提取的有用信号结合步骤（1）中的趋势项进行信号重构，实现重力数据的信噪分离。2仿真实验及工程应用

2.1 仿真实验

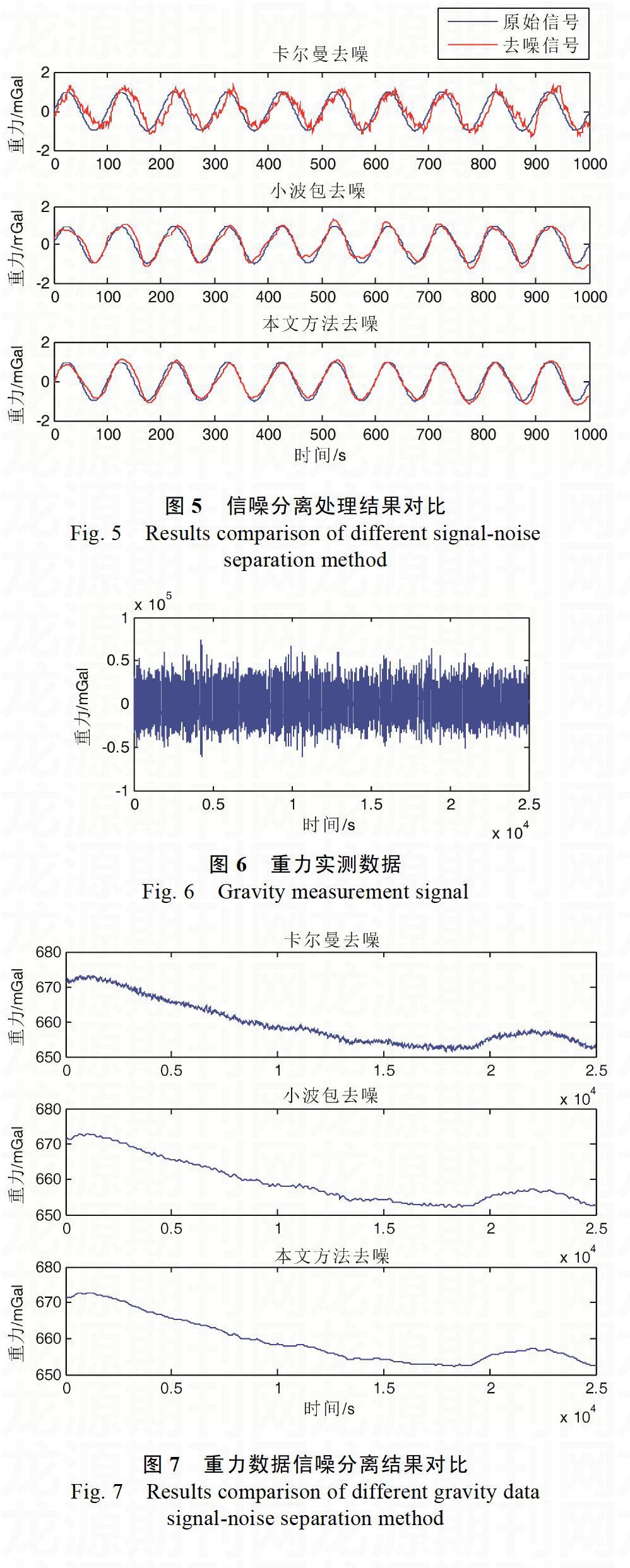
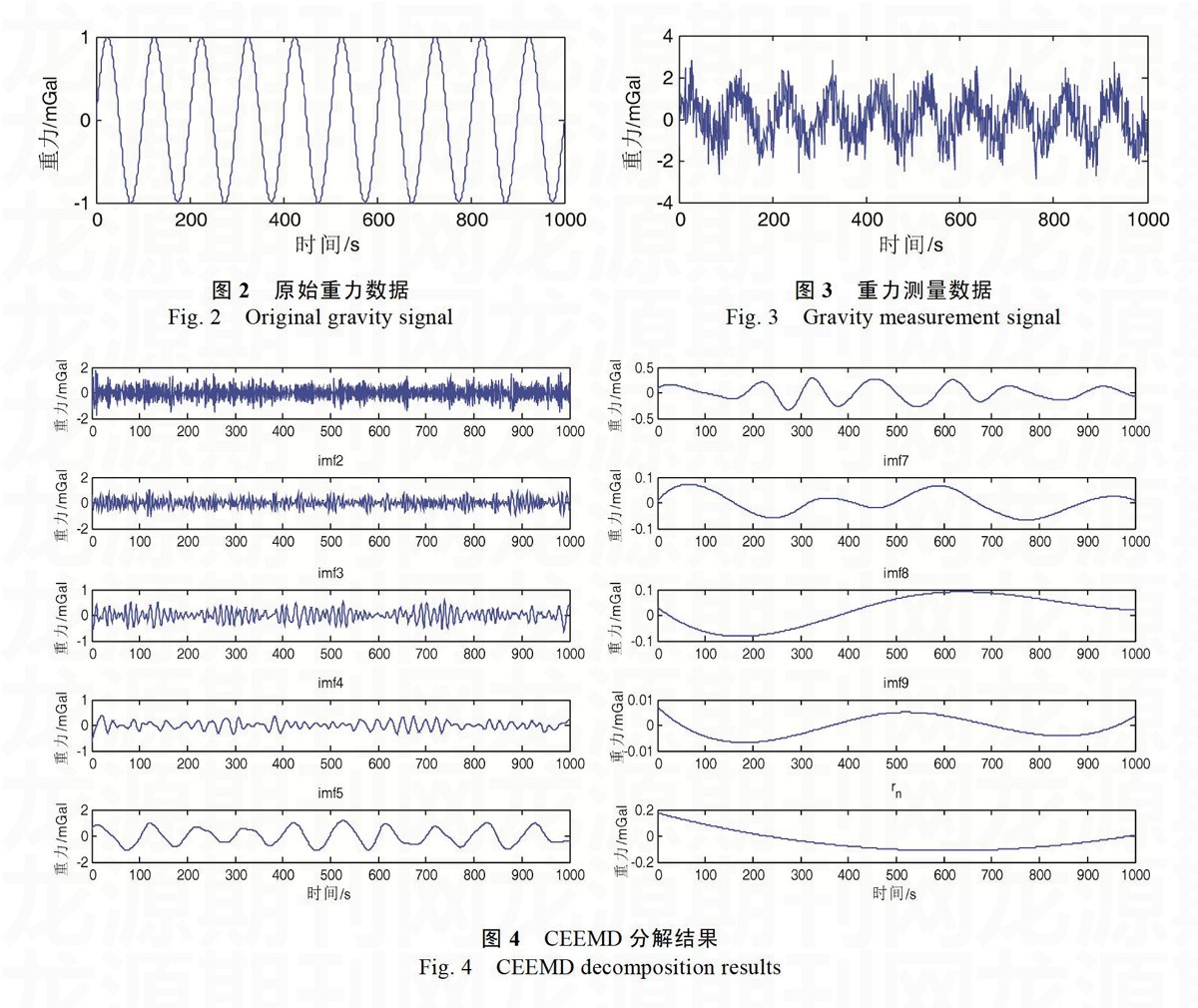
利用MATLAB对本文提出的基于CEEMD和小波包变换的信噪分离方法进行仿真。在仿真试验中，假设原始重力信号为低频正弦信号，该正弦信号幅值为1，频率为10Hz，如图2所示。通过在原始重力数据上加入一定量的噪声从而得到假设重力测量数据，如图3所示。对图3所示重力测量数据进行CEEMD分解，共得到9个IMF分量以及趋势项，分解如图4所示。

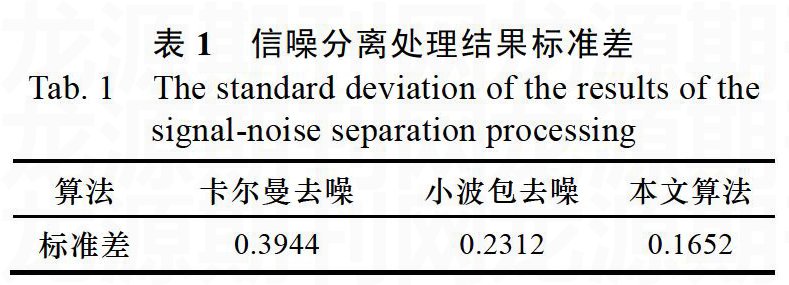
图5为本文提出的基于CEEMD和小波包变换的信噪分离方法与卡尔曼滤波以及只进行小波包去噪的结果对比图。由图5及表1可知，基于CEEMD和小波包变换的信噪分离方法所获得的信号与原始重力基准信号的标准差最小，说明该方法获得的波形与原始信号最接近，去噪效果最好，验证了该信噪分离方法的有效性。

2.2 工程应用

利用实测的海洋重力数据来检测本文所提出的重力测量信号信噪分离方法在实际工程应用中的有效性。某海区测线实测重力数据如图6所示，根据上文所述的信噪分离算法步骤对图6所示信号进行处理。

图7所示是本文提出的方法对实测数据处理的结果和卡尔曼滤波和小波包去噪处理的结果对比，从图中可见，本文提出的方法处理的结果能有效抑制噪声干扰，保留有用的重力信号，相比其他两种方法能实现精度较高的信噪分离。

仿真分析和实测数据的处理结果表明，本文提出的基于CEEMD和小波包变换的信噪分离方法突破了常用滤波算法的应用缺陷，能有效的消除重力实测数据中的噪声，提取出有用重力信号，能够得到更高的精度和实际工程应用价值。

3 结论

常用的信噪分离算法，如传统的FIR和IIR低通滤波、基于系统模型的卡尔曼滤波和H∞滤波算法以及基于矩阵理论的奇异值分解滤波等等，在处理含有大量噪声的海洋重力测量信号时难以取得更高的精度。为了有效地进行海洋重力测量信号的信噪分离，本文提出了基于CEEMD和小波包变换的信噪分离方法，并通过仿真数据和实测数据对该方法进行了验证。理论仿真分析和试验处理结果表明，对于重力实测数据，采用上述相关算法得到的重力信号，能有效抑制重力测量噪声信号并恢复重力信号，获得比较好的信噪分离效果，与只采用卡尔曼滤波或小波包去噪算法的重力信号处理算法相比，本文的信噪分离方法获取的海洋重力数据精度较高。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。