网站首页  词典首页

请输入您要查询的论文：

　

标题 基于FORTRAN的3D等效结点荷载计算
范文 司马丹琪++李元松++姜成潼++何泉

摘要： 在有限单元分析中，需将作用于单元的外力按虚功等效原则，移置到结点上成为等效结点力。由于数学运算的困难，往往限制了工程技术人员运用有限单元技术分析实际具有分布力的工程问题。以常用空间20结点单元为例，详述荷载等效过程，附注自编FORTRAN程序。并利用FEA软件进行计算对比验证程序正确性，为学者学习温度、预应力等类似工程问题的等效结点荷载计算提供有益参考。
Abstract： Abstract： In the finite element analysis， the external force acting on the element needs to be transferred to the node as the equivalent node force according to the principle of virtual work equivalence. Due to the difficulty of mathematical operations， engineers and technicians are often limited to use finite element technique to analyze practical distributed engineering problems. Taking the commonly used space 20-node element as an example， the equivalent process of load is described in detail. The software FEA is used to calculate and compare the correctness of the program， which provides a useful reference for scholars to study the equivalent nodal load of temperature， prestress and other similar engineering problems.
关键词： 离散体；等效结点荷载；虚功原理；程序设计
Key words： discrete body；equivalent node load；virtual work principle；program design
中图分类号：TP311.1 文献标识码：A 文章编号：1006-4311（2018）08-0233-020 引言
在弹性介质静力问题的计算中外加作用因素很多，如集中力、分布力（包括引力、斥力等场力、惯性力一类体积力和面积分布的由力边界条件给定的接触力）等直接载荷，也可能有因为温度改变、装配因素、预应力作用等其它干扰力[1]。这些外加作用因素都可遵循力学等效原则（如静力等效、位移模式下的虚功等效）处理成结点载荷。这种等效处理往往涉及较为复杂的坐标变换运算[2]，对于非力学专业的工程技术人员而言，存在一定困难。并且由于计算机语言的限制，传统的有限元程序设计课程只能以二维有限元问题为例介绍程序设计过程，极少涉及三维有限元的编程。而实际工程问题无一不是三维问题，因此编写三维程序更具有实际价值。现有商业计算软件中边界处理条件功能均很强大，但很难涵盖工程实际中遇到的各种边界条件问题，一旦遇到软件中没有对应的处理方法，仍需根据工程条件自行开发程序解决。笔者在有限元程序系统（FEM-PS）开发过程中，对3D等参单元等效结点荷载的计算公式进行详细推导，并利用FORTRAN程序设计成通用模块，以期对类似问题的解决有所启示。本文以三维空间二十结点等参单元为例，介绍FORTRAN语言在程序设计中的使用，并针对三维空间设计过程中的等效结点荷载计算环节做程序详述。1 等效结点荷载计算原理
1.1 集中力
设在单元内部或边界上任意点C（x，y，z）作用有集中荷载{Q}=[Qx，Qy，Qz]T，转化成等效结点荷载列阵{PE}（e）。根据转换前后虚功相等原则有[3]：
{PE} （e）=[Nc]T{Q}（1）
式中[Nc]为形函数在C点的值。
1.2 体积力
设单元内作用有均布体积力{p}=[px，py，pz]T，则可将单元微分体积dV上的体力{p}dV视为集中荷载，利用式（1），在单元的体积V内积分，即得到该分布体积力的等效结点荷载{PE }
1.3 表面力
设在单元的某边界面上作用表面力{ }={ ， ， }T，可将微分面积dA上的面荷载{p}dA视为集中荷载，利用式（1）在面积A上积分，即得到该分布面荷载的等效结点荷载{PE}
式中Ni表示单元的形函数，对于空间六面体20结点单元，其表达式为：
由于工程实际中给出的表面力往往是沿作用面的法向力和切向力，对于空间问题，外力往往垂直作用于边界表面，以？孜=1的面为例，载荷集度以 0表示，{PE} （e）表达式变为[4]
在计算结点荷载向量时由于被积函数比较复杂，常采用三维高斯积分公式[5]求解：2 FORTRAN的程序实现
作用在单元上的面力在等效成结点荷载的过程中，由于坐标轴的确定，力所作用面的方向会发生相应的变化。本文对三维二十结点的六个空间面进行编号，新定义变量NOACE（*）来表示力作用的單元面；将力作用面固定，如EXISP=-1.0（ξ=-1.0），再利用FORTRAN程序内部存储各面形函数顺序数组，如NFACE=（/1，9，5，20，8，12，4，16/），确定空间六面体结点拓扑关系：
IF（NOACE.EQ.1） THEN ！面力作用单元面的选择
NFACE=（/1，9，5，20，8，12，4，16/）
EXISP= -1.0
最后调用其他公共子模块矩阵[6]，求解分布面力的等效结点荷载。利用断点法对程序进行调试过程中，单元在受均布面力作用下进行等效之后，四周角点的等效结点荷载变为-1/12q，边中点变为1/3q，所述规律与文献[7]中相符。面力等效程序如下：
LGASH=（NFACE（IODEG）-1）*NDOFN+1 ！确定结点自由度编码
MGASH=（NFACE（IODEG）-1）*NDOFN+2
NGASH=（NFACE（IODEG）-1）*NDOFN+3 ！荷载等效
ELOAD（NEASS，LGASH）=ELOAD（NEASS，LGASH）+SHAPEI（NFACE（IODEG））*PXCOM* WEIGP（IGAUS）*WEIGP（JGAUS）
ELOAD（NEASS，MGASH）=ELOAD（NEASS，MGASH）+SHAPEI（NFACE（IODEG））*PYCOM*WEIGP（IGAUS）*WEIGP（JGAUS）
ELOAD（NEASS，NGASH）=ELOAD（NEASS，NGASH）+SHAPEI（NFACE（IODEG））*PZCOM* WEIGP（IGAUS）*WEIGP（JGAUS）3 實例及分析
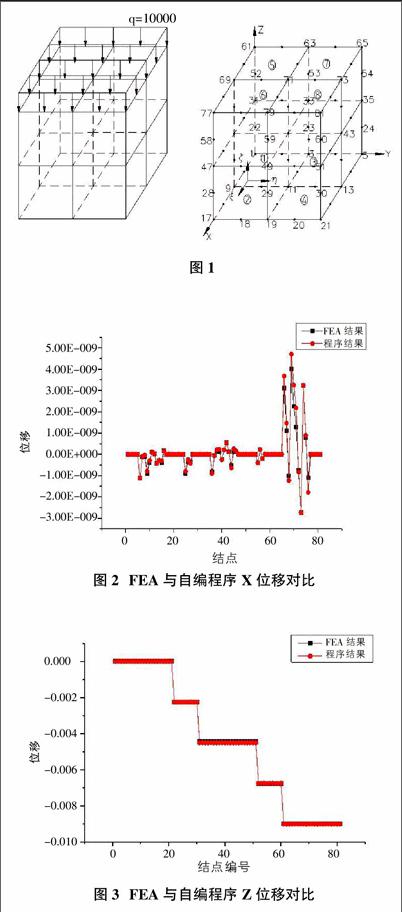
某空间正方体压力盒各边长为2.0m，上端面受均布面力荷载q=10.0kN/m2，其余面均固定，E=2.0×105MPa，μ=0.2，体密度ρ=50.0kN/m3，采用20节点等参单元，单元个数8，节点总数81。（图1）
为验证程序的正确性，在划分相同网格的条件下，取有限元软件FEA计算结果与程序计算结果做比对，如图2、图3所示。
由图2、图3的对比分析可知，用FORTRAN编制的程序计算结果与利用FEA模拟出来的结果基本吻合，说明了编制程序的正确性。4 结语
有限元商业软件的核心仍旧是有限元算法，只有掌握相应的逻辑流程及算法原理才能熟练操作一款软件，解决遇到的棘手问题。文章基于虚功原理推导了弹性问题空间20结点单元等效结点荷载计算公式，利用FORTRAN语言，设计成通用模块程序。采用算例验证算法与程序的正确性，为类似连续介质体问题的有限元法求解提供有益的参考。
参考文献：
[1]徐芝纶.弹性力学简明教程[M].三版.北京：高等教育出版社，1983.
[2]王勖成.有限单元法[M].北京：清华大学出版社，2003.
[3]赵更新，等.土木工程结构分析程序设计[M].北京：中国水利水电出版社，2001.
[4]王元汉，李丽娟，李银平，等.有限元基础与程序设计[M].广州：华南理工大学出版社，2002.
[5]朱加铭，欧贵宝，何蕴增.有限元与边界元法[M].哈尔滨：哈尔滨工程大学出版社，2002.
[6]Hinton E and D R J. Finite Element Programming[M].London： Academic Press，1977.
[7]朱伯芳.有限单元法原理与应用[M].二版.北京：中国水利水电出版社，1998.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 21:43:20