网站首页  词典首页

请输入您要查询的论文：

　

标题 基于人工神经网络过闸流量模型在南水北调中线工程的应用
范文 陈晓楠+段春青+郭芳+马艳军


摘要：南水北调中线工程线路长，沿线节制闸、分水口多，调度技术复杂，设计采用自动化调度模式。过闸流量的计算是自动化水量调度模型的重要组成部分，对于确定闸站实质是建立该闸的过闸流量与闸前、后水位，以及闸门开度的非线性函数关系。传统方法是利用经验公式进行计算，并在运行过程中，根据实测数据适时进行参数率定，人工对流量系数进行修正，需修改计算程序的源代码，缺少灵活性和智能性。基于人工神经网络，并结合传统水力学法建立过闸流量模型，该模型利用实测数据自动生成和更新各相关因素的与流量系数的函数关系，再通过流量系数计算过闸流量。经南水北调中线闸站的实例应用表明，该方法适应性强，具有很强的自学习能力和很高的拟合精度，并且较好地提高了泛化能力，使用方便，有推广应用的价值。
关键词：南水北调；神经网络；过闸流量
中图分类号：TV68文献标志码：A文章编号：
1672-1683（2015）001-0153-04
Application of discharge model by artificial neural networks in South-to-North Water Diversion Middle Route
CHEN Xiao-nan1，DUAN Chun-qing2，GUO Fang1，MA Yan-jun1
（1.Administration of South-to-North Water Diversion Middle Route Project，Beijing 100038，China；2.Beijing Water Affairs Centre for Suburbs，Beijing 100073，China ）
Abstract：The technology of water dispatch is very complex in South-to-North Water Diversion Middle Route Project，and it is necessary to take advantage of automation system for water delivery.The model for calculating flow rate is important to automation soft system，but traditional method needs often verify parameters by manual.A model of artificial neural networks is established to describe the relation between water level，gate opening and flux.The model finds the optimal function between water level，gate opening and flux coefficient by networks，and calculates flux by the coefficient.Take the new method into south-to-north water diversion middle route project，and compare neural networks model with traditional methods.Results show that the genetic programming model has high accuracy and is effective.
Key words：South-to-North Water Diversion Projet；neural networks；flow rate
南水北调中线干线工程自丹江口水库引水，经河南、河北、北京、天津四省市，总长1 432 km，以明渠为主，北京段采用预应力钢筒混凝土管和暗涵输水，天津干线采用暗涵输水。工程沿线设有64座节制闸，97座分水口门，设计多年平均调水量95亿m3。南水北调中线工程输水线路长，沿线分水闸门多，且无调蓄水库，调度技术难度大，设计上采用自动化调度模式，即根据实时采集的水情数据，利用自动化水量调度模型进行分析计算，实时生成调度指令，自动调整闸门开度。过闸流量的分析计算是水量调度模型的重要组成部分之一，目前设计单位采用的是传统的水力学方法，利用闸孔出流或堰流的经验公式和经验系数进行计算。在工程初期运行时，由于缺少实测水情资料，只能根据经验选取流量公式中的相关系数，随着运行中数据的积累，通过实测数据，再对水力学参数进行率定。这种方式需要专业人员每隔一段时间汇总实测数据进行分析，重新率定经验系数，并且需在水量调度模型的源代码中进行修正，操作不便。
本文针对上述问题，提出基于人工神经网络的过闸流量计算模型。同时，考虑到工程在运行过程，渠道除了充、退水阶段外，正常输水阶段输水流量一般较为稳定，实测流量数据往往集中在较小范围，若直接通过神经网络建立水位、开度与过闸流量关系，一般仅能在此较小的范围取得较好的回归结果，超出训练样本区域后模型的泛化能力较弱。因此，本文利用神经网络建立水位、开度与流量系数的关系，再通过流量系数利用水力学公式计算过闸流量，既能够通过程序方便、高效地自动实现建模，又可以提高计算精度。
1BP人工神经网络模型
人工神经网络（Artificial Neural Networks）起源于人们对生物的神经网络的研究，是一种先进的数据挖掘技术。人工神经网络，又被称之为连接主义模式，通过大量简单的神经元互相连接组成大规模的并行分布式信息处理和非线性动力学系统，根据已有的输入、输出样本，基于某种网络训练算法对网络进行训练。训练成功后即可根据输入数据直接推算输出结果，最常用神经网络是BP神经网络，在建模、预测、控制等多个领域得到了成功应用[1-3]。
采用误差反馈算法进行网络训练的神经网络称之为BP神经网络，假设建立的神经网络共三层：即输入层、隐含层和输出层。设输入层神经元的维数维，输出层神经元的维数为维，隐含层神经元的维数为。BP神经网络的训练方法具体如下[4-6]。
假设隐含层与输出层的各神经元的连接权矩阵为W，wij表示隐含层中第i个神经元与输出层中第j个神经元之间的权值，i=1，2，…，h；j=1，2，…，m。输入层与隐含层的各神经元的连接权矩阵为V，vij表示输入层中的第i个神经元与隐含层中第j个神经元之间的权值，i=1，2，…，n；j=1，2，…，h。
设（X，Y）为样本集中的一个样本，X=（x1，x2，…，xn），Y=（y1，y2，…，ym），并选取激励函数为
f（net）=11+e-net（1）
通过激励函数、连接权矩阵以及输入样本计算出的输出向量为：O=（o1，o2，…，om），隐含层的输出向量为：O′=（o′1，o′2，…，o′h），具体如下
oj=f（netj）=f（∑hi=1wij·o′i）j=1，2，…，m（2）
o′j=f（net′j）=f（∑ni=1vij·xi）j=1，2，…，h（3）
则针对该样本的测度误差可由下式计算：
E=12∑mk=1（yk-ok）2（4）
则对样本集中，每个样本的测度误差求和得到整个样本集的测度误差∑E。
利用负梯度方向下降法调整连接权重，隐含层与输出层连接权wij的调整量Δwij可由下式计算：
Δwij=αδjo′i=α（yj-oj）（1-oj）·oj·o′i（5）
式中：α为学习效率，为事先给定常数，如取0.5。
输入层与隐含层连接权的调整量Δvij由下式计算：
Δvij=α∑mk=1（δk·wjk）·（1-o′j）·o′j·xi
令=∑mk=1（δk·wjk）·（1-o′j）·o′j=δ′j
则Δvij=α·δ′j·xi（6）
重复上述过程，直至整个样本集的测度误差很小，或者超出事先给定的循环次数。
2神经网络过闸流量模型
根据闸孔出流水力学计算公式，过闸流量可由下式进行如下计算：
Q=σsμbe2gH（7）
式中：Q为过闸流量（m3/s）；σs为淹没系数，与闸前、闸后水位有关；μ为流量系数，与闸门开度有关；b为闸室底宽（m）；e为闸门开度（m）；H为闸前水头（m）。把淹没系数和流量系数合并成一项，称为综合的流量系数m：
m=σs·μ（8）
则闸孔出流过闸流量公示简化为
Q=mbe2gH（9）
对于明确的节制闸，其闸室宽度固定，流量系数m是闸门开度、闸前水位、闸后水位的函数。在输水运行过程中，可以实时获取水位、开度和实测流量的数据，则可由下式计算流量系数样本：
m=Qbe2gH（10）
将节制闸的闸门开度、闸前水位、闸后水位数据作为输入样本，将根据实测流量计算的流量系数作为输出样本，利用上述BP神经网络自动建立模型，之后，即通过模型根据给定的闸门开度、闸前水位、闸后水位计算流量系数，进而计算出过闸流量。
3算例
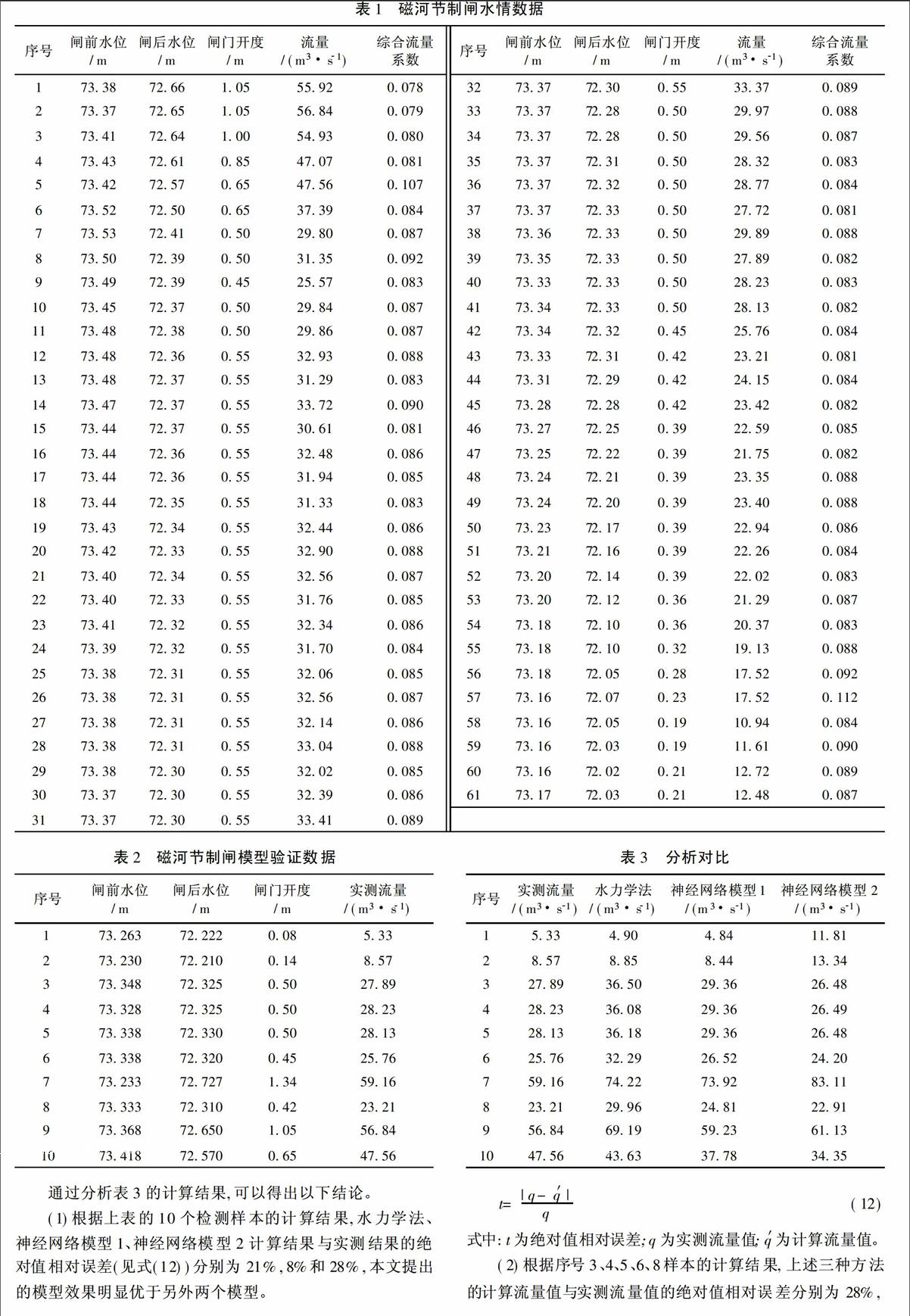
南水北调中线工程设置64座节制闸，每座节制闸均设置了流量计，本文选取京石段工程的磁河节制闸为例来验证模型。磁河节制闸设有3孔闸门，每孔宽度6 m，弧形闸门。磁河节制闸某一时段的水位、开度（3孔开度均相同）、流量（3孔闸门过闸流量）实测数据见表1。
利用人工神经网络和上表数据建立模型，网络设3层，输入层神经元个数为3，分别对应于闸前水位、闸后水位以及闸门开度数据；输出层神经元个数为1，对应于流量系数；隐含层神经元根据多次试算，设定为5，学习效率取0.5。为了计算方便，通过下列公式（11），将输入数据进行归一化处理，输出数据本身就是介于0至1之间，因此，不必转化。
z′=zzmax（11）
式中：z′为归一化处理后的数据；z为原始数据；zmax为最大数据，对于闸前、闸后水位可以取该节制闸的设计水位；对于闸门开度，则可以选取闸前设计水位下的水深。磁河节制闸设计水位73.88 m，设计水位下闸前水深7.16 m。使用VB 60编写了通用程序，经计算，输入层至隐含层权矩阵，隐含层至输出层权矩阵分别为
-0.5190.906-0.217-1.000-0.436
0.6980.048-0.698-0.599-0.176
0.3730.5930.2900.2920.813
-0.584-1.737-0.9540.160-1.431
利用其他的磁河过闸流量数据，作为检验样本对模型进行验证见表2。
分别利用本文建立的模型（简称“神经网络模型1”）、传统水利学闸孔出流模型，以及直接建立闸前、闸后水位、闸门开度与实测流量的神经网络模型（简称“神经网络模型2”），进行对比。在利用神经网络模型2时，流量数据的归一化处理中的zmax取设计流量值，磁河节制闸为165 m3/s。计算结果见表3。
表1磁河节制闸水情数据
通过分析表3的计算结果，可以得出以下结论。
（1）根据上表的10个检测样本的计算结果，水力学法、神经网络模型1、神经网络模型2计算结果与实测结果的绝对值相对误差（见式（12））分别为21%，8%和28%，本文提出的模型效果明显优于另外两个模型。
表3分析对比
t=|q-q′|q（12）
式中：t为绝对值相对误差；q为实测流量值；q′为计算流量值。
（2）根据序号3、4、5、6、8样本的计算结果，上述三种方法的计算流量值与实测流量值的绝对值相对误差分别为28%，5%，5%，神经网络方法明显高于水力学方法。对照这些检测样本与表1中的训练样本，会发现这几个检测样本与训练样本中的一些样本很相似，这说明神经网络有很好的拟合能力，当检验样本与训练样本接近时，能得出很好的结果。但是，其泛化能力较弱，所以对与训练样本相差稍大时，用神经网络模型2计算结果就不理想了。但本文建立的神经网络模型1将神经网络和水力学经验公式法相结合，通过神经网络拟合流量系数，再利用水力学公式进行流量计算，提高了泛化能力。
（3）表3中序号7样本计算结果与实测流量的误差最大，三种方法的绝对值相对误差分别为25%，25%，40%。对照该样本和训练样本可以发现，该样本与训练样本中的数据偏差很大。对于训练样本中，闸前水位在73.2 m附近，闸后水位一般在72.2 m附近，但开度数据一般在0.4 m附近，而检验样本中的序号7样本的开度为1.34 m，超出3倍多，因此，计算结果偏差较大。但是，随着工程运行过程中，样本数据的不断丰富，基于神经网络的模型有很强的自学习能力，将会根据更新的数据自动调整模型结构，使得计算结果越来越优。
4结语
本文基于人工神经网络结合传统水力学方法，建立过闸流量计算模型，该模型利用神经网络建立水位、开度和流量系数的回归关系，并再由流量系数和闸孔出流模型计算过闸流量。该模型能够自动根据样本数据进行自学习，更新模型结构，同时较好的提高了泛化能力。通过实例表明：该模型具备强大的自学习能力，能够自动建立模型；具有很好的拟合能力，拟合精度高；较好的提高了模型泛化能力，提高了计算精度；使用方便，适应性强，有推广应用的价值。
参考文献：
[1]蒋宗礼.人工神经网络导论.[M]高等教育出版社，2001.
[2]邱 林，陈守煜，聂相田.模糊模式识别神经网络预测模型及其应用[J].水科学进展，1998，9（3）：258-264.
[3]杨卫东，李伟娟.南宁站洪水期水位流量关系曲线的直接拟合[J].广西水利水电，2003，（3）：15-19.
[4]穆祥鹏，陈文学，崔巍，等.弧形闸门流量计算方法的比较与分析[J].南水北调与水利科技，2009，7（5）：20-22.
[5]姜万录，雷亚飞，张齐生，等.基于神经网络软测量的动态流量测量方法研究[J].流体传动与控制，2007（6）：25-30.
[6]金菊良，魏一鸣，杨晓华.基于遗传算法的神经网络及其在洪水灾害承灾体易损性建模中的应用[J].自然灾害学报，1998，7（2）：53-60.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/5 22:09:11