《基于PSO-Elman神经网络的深基坑变形预测研究》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

基于PSO-Elman神经网络的深基坑变形预测研究

范文

谢冬冬张慧江

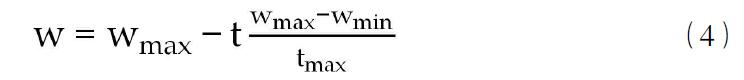
摘要：深基坑工程的稳定性和安全性受到全社会的普遍关注，而深基坑变形预测是施工中调整施工参数和保证施工安全的重要手段。文章构建粒子群优化Elman神经网络的深基坑变形预测模型，克服了由于Elman神经网络初始化权阈值的盲目随机性而造成的收敛速度慢、易陷入局部极小等不足，预测精度较Elman模型有显著提高，能够满足工程实际应用的需要。

Abstract： The stability and safety of deep foundation pit projects have received widespread attention from the whole society， and the prediction of deep foundation pit deformation is an important means of adjusting construction parameters and ensuring construction safety during construction. This paper builds a particle swarm optimized Elman neural network deep foundation pit deformation prediction model， which overcomes the shortcomings of slow convergence and easy fall into local minima due to the blind randomness of the initialization threshold of the Elman neural network. The prediction accuracy is significantly improved than the Elman model， and can meet the needs of practical engineering applications.

关键词：深基坑工程;变形预测;PSO-Elman网络模型

Key words： deep foundation pit;deformation prediction;PSO-Elman network model

中图分类号：TU753 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文献标识码：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章编号：1006-4311（2020）17-0120-03

0 ?引言

地下空间的开发利用受到人们越来越多的关注，涌现了大量的深基坑工程，确保基坑施工安全成为其的首要任务。而深基坑变形预测在调整施工方案和规避施工风险中具有重要实用价值，是保证施工安全的重要措施[1]。数值模拟法是应用较多的传统的深基坑变形预测方法，但由于基坑工程本身的不确定性和复杂性，使基坑变形预测精度受到影响，系统分析方法被引入到深基坑工程中，并得以广泛应用[2-4]。常用的系统分析方法主要有时间序列分析、灰色系统理论、遗传算法及人工神经网络等[5-6]。其中人工神经网络具有很强的自适应和自学习能力，对基坑监测获取的波动较大和非线性的数据具有较好的预测效果[7-8]。但神经网络初始化权阈值具有盲目随机性，从而导致的收敛速度慢、易陷入局部极小。利用具有全局寻优能力的粒子群算法来對神经网络的权阈值进行优化，改善其性能，提高深基坑变形预测精度。

文章采用粒子群算法来优化Elman神经网络的初始权阈值，构建PSO-Elman神经网络的深基坑多类数据预测模型，将监测点围护墙坡顶水平位移量为输入向量，来对其15m深度处桩身深层水平位移量进行预测，提高预测精度。

1 ?基坑变形预测方法的基本理论及原理

1.1 Elman神经网络

Elman神经网络由Elman于1990年提出，是一种典型的动态反馈型神经网络[9-11]。Elman网络结构一般分为4层;输入层、隐含层、结构层和输出层，其模型结构如图1。

Elman网络的非线性状态表达式为

（1）

式中，t表示时刻，xct表示结构层输出，ut-1为输入层的输入向量，x（t）为隐层的输出，yt为输出层的输出，w1、w2与w3分别表示结构层到隐层、输入层到隐层和隐层到输出层间的联接权值矩阵，θ（1）、θ（2）分别为隐层和输出层的阈值，f（·）、g（·）分别表示隐含层、输出层的激活函数，f（·）多采用S型函数、g（·）一般采用函数Pureline函数。

1.2 PSO算法

PSO算法源于对鸟群飞行觅食的行为的模拟，是一种简单高效的全局优化算法[12-14]。其采用速度-位置搜索模型，每个粒子可以看做没有质量与体积但具有位置和速度的点，粒子在可行解空间以一定的速度进行搜索，飞行速度根据飞行经验进行动态调整。假设m个粒子构成D维搜索空间的一个群体，第i个粒子在d维空间中的所处的当前位置为Xi=（xi1，xi2，…，xid），飞行速度为Vi=（vi1，vi2，…，vid），Pi=（pi1，pi2，…，pid）为第i个粒子的个体最好位置，Pg=（pg1，pg2，…，pgd）为整个群体的最好位置。

PSO算法根据式（1）和式（2）来更新粒子的速度和位置：

（2）

（3）

式中，c1、c2为学习因子，一般设置，c1=c2=2，r1、r2为介于之间的随机变量，w为惯性权重因子，对算法全局和局部搜索能力起着平衡的作用，其调整采用线性递减权策略，其公式为

（4）

wmax、wmin分别为惯性权重的最大值和最小值，t为当前迭代次数、tmax为最大迭代次数。粒子初始位置和速度随机产生，按式（2）、式（3）进行更新，直至找到最优解。

1.3 PSO-Elman神经网络模型

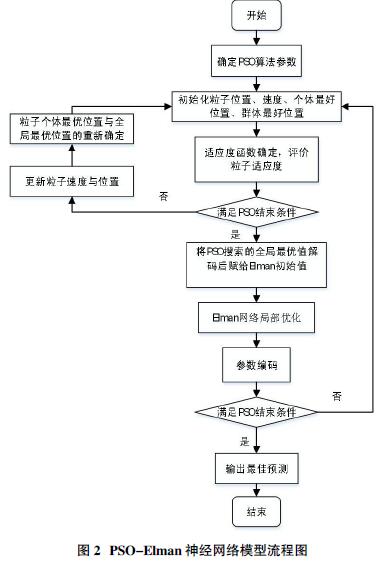
目前，Elman神经网络虽是一种重要类型的反馈型神经网络，但其算法普遍采用基于梯度下降误差反馈原理，这类算法往往存在收敛速度慢、易收敛于局部极小值和全局搜索能力差等不足。为克服这一缺点，将擅长全局搜索的PSO算法对Elman神经网络进行改进，建立粒子群优化的Elman神经网络模型[15]。该算法将Elman网络节点间的连接权值和阈值作为PSO算法中粒子的位置参数，采用PSO算法进行全局搜索，得到Elman神经网络的初始值，在进行局部优化。PSO-Elman神经网络的流程如图2。

粒子群算法优化Elman神经网络的流程图如图2。

2 ?实际工程应用

2.1 工程概况

选取某建筑深基坑监测工程，地块基坑周长为713m，埋深约6.9～19.9m，采用明挖施工形式，框架及剪力墙结构。拟建场地地基土层主要为两层：人工填土层（杂填土）和第四系冲洪积粘土、粉土、圆砾层。对整个开挖过程中的基坑变形进行了监测，其中围护墙坡顶水平位移和桩身深层（15m）水平位移每两天监测一次，共观测79期，选取19期为样本数据。

2.2 变形预测模型选取

文章选取J08、J28、J18、J34四个监测点围护墙坡顶水平位移为输入单元，J08'、J28'、J34'三个监测点的15m深度处的桩身深层水平位移为输出单元，将样本数据前14次监测数据作为训练样本的输入值和输出值，后5次数据作为预测样本的输入值与输出值。Elman神经网络采用4个输入单元和3个输出单元，中间层神经元个数为20。PSO算法种群大小为40，最大迭代次数为200。

2.3 预测结果

调用MATLAB人工神经网络工具箱来实现PSO算法对Elman网络的优化，并对J08'、J28'、J34'三个监测点深层水平位移进行预测，为增加对比，加入相同条件下Elman神经网络的预测结果。PSO-Elman网络水平位移预测值与实测值对比如图3。

由上述图表可以看出，PSO-Elman神经网络模型精度明显优于Elman网络模型，PSO-Elman模型预测最大相对误差为15.21%，平均相对误差为7.58%，Elman网络最大相对误差达到42.04%，平均相对误差为17.68%，但随着预测样本数的增加，预测精度会有所降低，为保证预测精度，PSO-Elman网络模型预测样本量不宜太长。

3 ?结论

针对Elman神经网络在深基坑变形预测中存在的问题，采用粒子群算法来优化Elman神经网络的初始权阈值，构建了PSO-Elman神经网络预测模型。实际应用表明，经粒子群优化后的Elman网络明显比Elman网络的预测精度高，在预测样本量较少时，能够有效运用于深基坑变形预测中。

参考文献：

[1]陈忠汉，黄书秩，程丽萍.深基坑工程[M].机械工业出版社，2002.

[2]刘志凯，郑毅，左广州.基坑开挖与土钉支护的数值模拟[J].吉林大学学报（地球科学版），2004（S1）：103-106.

[3]曹凈，普琼香，刘海明，李帅.土钉支护基坑开挖的动态规划方法研究[J].控制工程，2018，25（12）：2120-2127.

[4]陆新征，宋二祥，吉林，等.某特深基坑考虑支护结构与土体共同作用的三维有限元分析[J].岩土工程学报，2003，25（4）：488-491.

[5]袁金荣.地下工程施工变形的智能预测与控制[D].同济大学，2001.

[6]刘思峰，杨英杰.灰色系统研究进展（2004-2014）[J].南京航空航天大学学报，2015，47（01）：1-18.

[7]程宇也.基于人工神经网络的短期电力负荷预测研究[D].浙江大学，2017.

[8]孙海涛，吴限.深基坑工程变形预报神经网络法的初步研究[J].岩土力学，1998（4）：63-68.

[9]韩旭明.Elman神经网络的应用研究[D].天津大学，2006.

[10]梅贵琴.改进的Elman神经网络和网络参数优化算法研究[D].西南大学，2017.

[11]解小平.基于Elman神经网络的短时交通流预测及应用研究[D].兰州交通大学，2017.

[12]王维博.粒子群优化算法研究及其应用[D].西南交通大学，2012.

[13]蒋林利.改进的PSO算法优化神经网络模型及其应用研究[D].厦门大学，2014.

[14]涂娟娟.PSO优化神经网络算法的研究及其应用[D].江苏大学，2013.

[15]顾兆军，李冰，刘涛.基于PSO-Elman模型的网络流量预测[J].现代电子技术，2019，42（01）：82-86.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。