
摘 要:数学猜想是数学发现的萌芽,可以开启儿童的智慧之门。而数学解题是培养儿童数学猜想能力的重要载体。教学中,教师可以巧用“类比猜想”、智用“归纳猜想”、善用“审美猜想”、妙用“假设猜想”、运用“直觉猜想”、活用“综合猜想”等。通过引导学生进行数学猜想,培养学生的创新意识和创新能力,让学生成为一个数学意义上的“小创客”!
关键词:数学猜想;儿童智慧;创新能力
数学猜想是数学发现的萌芽。英国著名科学家牛顿曾经这样说,“没有大胆的猜想就不可能有伟大的发现和发明”。著名物理学大师爱因斯坦也曾这样说过,“想象力比知识更重要,因为知识是有限的,而想象力是无限的,它能概括世界上的一切并且推动着进步。”因此在数学教学中,教师不仅要教知识、教方法、教思想,更要教猜想。
所谓“数学猜想”,是指一种基于数学事实材料和数学知识而生发的大胆的、创造性的想象。数学猜想是以自我内隐的数学观念、思想、理论和方法等为指导,对某些特定的数学对象及其关系做出的一种推断、论断。运用数学猜想,学生可以产生新的解题思路、诞生新的解题方法、发现新的数学知识。因此,数学猜想不是“瞎猜”、不是“胡思乱想”,而是根据问题和条件的特质展开的合理想象。运用“数学猜想”,可以开启儿童的数学智慧之门。
一、巧用“类比猜想”
“类比猜想”是根据数学对象的已有条件的内涵、性质等,通过巧妙地类比,推出另一个对象可能也具有相似的问题解决策略、方法或相应结果。数学的类比猜想能够活化学生思维,是学生数学发现的重要手段。
例1:理发店里的王师傅有两条毛巾,既可以作为披肩用,也可以用作洗头。如果作披肩用,160天毛巾将破旧报废;如果用作擦头发,40天就报废。为了使用的天数尽可能多一些,王师傅交替着使用这条毛巾,即毛巾既作为披肩,又用作擦头发。那么一条毛巾最多可以用多少天?
分析:根据题目的文字表述,我们很容易就会发现,这一道题目的意思类似于“工程问题”。基于此,我们可以展开类比猜想,如“一项工程,甲单独做需要160天,乙单独做需要80天。现在两队合做,需要多少天可以完成这样的工程?”在这里,陌生化的数量关系被转化成熟悉的数量关系,其中的数学解题思路一目了然。因此,我们可以将一条毛巾的使用天数看作单位“1”,则作披肩用每天使用毛巾折旧,作洗头用每天使用毛巾折旧为,两种用法交替使用一天,即2天的折旧为+=。那么,要求一条毛巾交替使用最多可以使用多少天,就是求单位“2”里面有几个+=。类比猜想让数学问题得以巧妙解决。
因此本题可以这样列式:2÷+=64(天)。
二、智用“归纳猜想”
所谓“归纳猜想”,是指学生运用归纳法(完全归纳法和不完全归纳法)对研究对象或问题从一定数量的个例、特例、具体或全部例证中展开数学观察、数学分析,进而得出某些一般性的数学结论的猜想。运用“归纳猜想”的一般步骤为:观察—归纳—猜想—验证。
例2:在平面上画两条直线,会产生一个交点;在平面上画三条直线,直线与直线两两相交,会产生3个交点。那么,在平面上画100条直线,这些直线两两相交,一共会产生多少个交点?
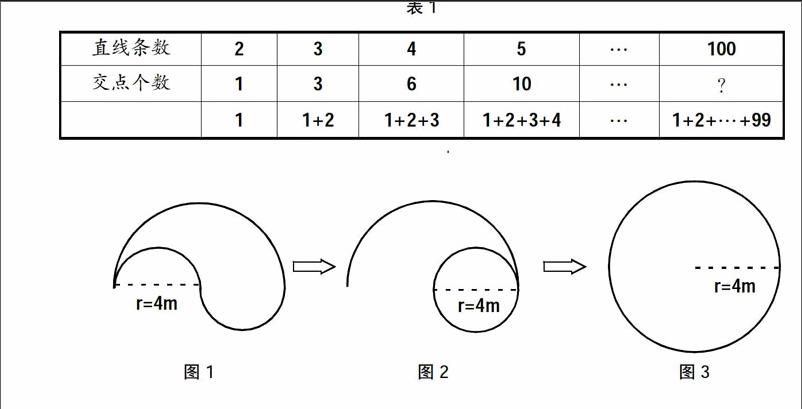
分析:这一道习题显然我们应该采用“不完全归纳法”来分析问题、解决问题。即从某类事物中的部分事物出发,探究部分事物的规律、性质或关系,进而推断出全体的规律、性质或关系等。这里一般用的是因果归纳,即在这个过程中,我们无须考虑对象的全体,而只需对部分对象展开数学观察、研究,进而得出数学结论。所以,不完全归纳中的因果归纳法要比完全归纳中的列举归纳更具思维活力。这里,数学观察和数学实验是展开归纳猜想的基础。在本题中,我们可以通过画图,列表(如表1)展开具体分析。
根据上述表格,不难发现浅表性的数学规律,即从1开始的若干个连续自然数的和。深入观察便会发现,如果直线的条数为n,那么交点的个数就是1+2+…+(n-1)。我们不禁要问,每一次增加的交点有没有什么规律呢?对了,每一次增加的交点个数是原来的直线数。这是为什么呢?因为每次增加一条直线都是在原有直线条数的基础上增加的,都要和原有直线相交。因此,增加的交点数就是原有直线的条数。
因此本题可以这样列式:1+2+3+…+99=4950(个)。
三、善用“审美猜想”
数学是一门美的科学。许多数学问题都有着简约美、奇异美、对称美、和谐美等。教学中教师要善于引发学生的“审美猜想”,通过学生的“美感思维”对数学问题用一种别样的策略来解决。在数学解题过程中,许多看似复杂、困难的问题,其解决策略却是简单的、充满美感的。
例3:求图1的周长。
分析:这是求一个不规则的图形的周长的问题。在解决问题的过程中,我们当然可以各个击破,分别求出三个“圆周长的一半”,然后相加,最后求出整个图形的周长。但其实我们可以对这个图形展开动态处理和“审美猜想”。如果将左边“小圆周长的一半”移至右边“小圆周长的一半”的上面,可以凑成一个小圆(如图2)。然后我们可以将小圆的周长往左拉,就可以形成右边的圆(如图3)。因此,本题中图1的周长也就是图3的周长。
因此本题列式为:C=2πr=8π(m)。
四、妙用“假设猜想”
假设猜想是指在数学猜想中运用“假设法”,根据数学问题的性质和条件的特点做出的一种先行于正确解答的数学猜想。假设猜想是一个多向思维的心理过程,具有经验性、跳跃性、主动性的特点。“假设猜想”犹如在大海捕鱼,虽然不能“竭泽而渔”、十拿九稳,但是依据自己的数学知识经验和解题经验,甚至一刹那的灵感都能做出一种即时判断。
例4:明明从山脚上山顶,每分钟行30米,从山顶沿着原路返回山脚,明明每分钟行50米。已知明明上山比下山多用了4分钟。那么,山脚与山顶的距离是多少米?
分析:由于题目中已知明明上山的速度和下山的速度以及上山与下山的时间差,而路程未知,导致本题看上去无从下手。不过复杂的问题背后考量的是数学猜想的智慧。在本题中,如果我们巧妙设数,对山脚与山顶的距离进行合理、巧妙地赋值,即把未知数量具体化,则或许可以让问题快捷地解决。据此,我们用假设法展开合理的数学猜想。根据明明上山的速度是每分钟30米和下山的速度是每分钟50米,我们可以假设山脚和山顶的距离是150米(30和50的最小公倍数)。接着我们可以检验猜想,当山脚与山顶的距离是150米的时候,上山比下山多用了150÷30-150÷50=2分钟。而题目中明明上山比下山多用了4分钟,所以我们要调整猜想。因为4÷2=2,所以我们就再次假设山脚与山顶的路程为150×2=300米。再次检验我们的假设:300÷30-300÷50=4分钟,与题目条件相符。
因此本题的正确结果是300米。
五、运用“直觉猜想”
在数学学习中,许多学生往往能够迅速解决问题,这体现为一种深刻的洞见。其中,直觉猜想往往发挥着重要的作用。著名物理学家爱因斯坦说,“我信任直觉。”在解决数学问题的过程中,我们应当首先对解题结果或解题过程有一个大致的估测,这是一种以直接的、跨越式的方式整体地把握问题、直接获取答案的过程。学生依凭自己的数学知识和数学想象力往往能够大致确定问题的结果范围。
例5:如图4,在梯形ABCD中,△AOD和△BOC两个阴影部分的面积相比( )(a大、b大、一样大)。
分析:数学直觉洞察力是评价学生数学才能的一个重要标准。在本题中,我们凭借直觉认为△AOD和△BOC的面积相等。当然,这种依靠直觉的数学猜想开始是无效果的,如何“有效地证明”呢?在数学直觉猜想的引导下,我们会发现△ADC和△BDC是同底等高的三角形,因此△ADC和△BDC的面积是相等的。那么,△AOD、△BOC与△ADC、△BDC之间有没有什么关系呢?不难看出△ADC的面积比△AOD的面积多了一个△ODC,而△BDC的面积比△BOC的面积也多了一个△ODC。因此,从△ADC和△BDC中分别减去一个△DOC的面积,剩下的△AOD和△BOC的面积也就分别相等。
因此,本题中△AOD和△BOC的面积相等。
六、活用“综合猜想”
很多时候,猜想并不是单一的,而是综合了类比、归纳与假设等多种数学猜想方法。首先是要教给学生基本的数学猜想方法,在学生掌握了基本数学猜想方法后,要引领学生进行综合猜想,培养学生的综合猜想能力。通过一定的题目诱导学生进行类比、联想,不断开阔学生的解题思路、解题方法,形成学生的解题思想。
分析:这道题目如果将分母算出来,然后通分简直不可思议。因为分子都是1,所以我们还应该从分母处展开联想。熟练的分数加减法的经验告诉我们,这道题可以和“裂项相消法”类比起来,将题目中的所有的项的乘积形式都改写成差的形式:如1-=,-=,…,-=。接着可以让学生展开归纳猜想,=(-)。然后将上述题目中的每一项都写成两个分数的差的形式。最后将分母是积的形式转化成分母是差的形式。
因此,本题的正确解法是:
数学猜想能力是学生数学认知中最活跃、最具创造性的因子,它不是一朝一夕能形成的,而是需要教师长期的悉心培养。因此数学教学中,教师不能简单而机械地传授知识,而应将学生的数学猜想融入知识的生成过程中,融入数学的解题过程中。只有这样,才能萌发学生的创新意识,培养学生的创新能力,让学生成为一个数学意义上的“小创客”!
- 百岁老人的入党初心
- 金秋送爽话菊花
- 九十年前一场电车文明与人力车夫的冲突
- “网”课学习不新鲜
- 近代北京第一座无线广播电台
- 两份珍贵的档案
- 美国高校档案馆面向研究型用户的网络服务介绍及启示
- 比照中外档案馆,凸显公共性趋势
- “中国天眼”档案管理实践探索研究
- 企业历史遗留问题档案清理策略研究
- 家族档案征集与利用探析
- 档案库房虫害与霉变防治研究
- 《企业数字档案馆(室)建设指南》内容及相关问题思考
- 关于新技术热潮下在档案领域应用区块链技术的冷思考
- 境外工程档案标准化管理规范探究
- 谈人类意识形态与档案
- 《档案著录规则》(GB/T18—1999)的对比研究和修订建议
- 东城区档案局(馆)完成“不忘初心、牢记使命”主题教育领导小组文件材料归档工作(16则)
- 北京战“疫”行动摄影大赛评选结果及部分获奖照片展示
- 怀柔古城竹马会
- 档案中的中华全国体育协进会
- 晚清北京画报与女性社会生活管窥
- 北京历史上第一家卫生类博物馆
- 民国年间北京的抗疫斗争
- 抗疫视角下的历史片段
- prat
- prats
- prattle
- prattled
- prattlement
- prattlers
- prattles
- prattling
- prattlingly
- prawn
- prawned
- prawner
- prawners
- prawning
- prawns
- pray
- prayable
- prayed
- prayer
- prayerlessly
- prayerlessness
- prayerlessnesses
- prayerlessness's
- prayers
- prayerwise
- 夭折,早死
- 夭折,短命
- 夭摧
- 夭斜
- 夭昏
- 夭昏札瘥
- 夭昬
- 夭札
- 夭枉
- 夭桃
- 夭桃
- 夭桃秾李
- 夭桃襛李
- 夭椓
- 夭横
- 夭死
- 夭殁
- 夭殂
- 夭殇
- 夭殈
- 夭没
- 夭疫
- 夭疾
- 夭矫
- 夭矫不群