《一种改进的线性递减权值的粒子群优化算法》-工学论文，通信论文-论文范文参考-科学狗论文网

标题

一种改进的线性递减权值的粒子群优化算法

范文

崔新于+田梓君

摘要：针对粒子群优化算法的早熟问题，在线性递减权值的粒子群优化算法的基础上，提出了一种增强粒子多样性的粒子群算法，有效减少了粒子的无效迭代。实验结果表明，该算法具有较高的收敛精度，能有效避免早熟收敛问题。

关键词：粒子群优化算法；线性递减权值；平均值；早熟收敛；全局优化

粒子群优化算法（Particle Swarm Optimization，PSO）[1]自1995年提出以来，得到了广泛关注和应用。基本粒子群算法容易陷入局部最优[2]，寻优性能差。相关学者已经提出了很多的改进方法，第一类改进是引入惯性权值w并使其线性递减的PSO（线性递减权值PSO）[3-4]；第二类改进是粒子群优化算法与其他算法相结合。仍然无法解决早熟问题。

本文在线性权值递减的基础上提出了一种新的改进方法，使得粒子群优化算法的寻优性能得以提高。在线性递减的基础上，加入判断早熟停滞的方法，一旦粒子群优化算法陷入局部最优，便将之前的寻优结果相加求平均值作为当前的粒子，再继续进行寻优。试验结果表明文章算法在很大程度上提高了粒子群优化算法的寻优性能。

1 相关问题描述

线性递减权值的PSO算法公式如下：

其中；表示粒子i第k次迭代的速度矢量的第d维分量；表示粒子i第k次迭代的位置矢量的第d维分量；c1、c2是学习因子，通常c1=2，c2=2；r1、r2是分布于[0，1]范围内的随机数， wmax表示惯性权值的最大值，wmin表示惯性权值的最小值，kmax表示最大迭代次数。算法在运行过程中，粒子的个体最优值和粒子群的全局最优值都不断更新，算法结束时，输出全局最优值gbest。

在本文算法中，如果当前粒子的位置存在与之前粒子相同的现象，则可以认为当前粒子的迭代为无效迭代，按照式（4）改变当前粒子的位置以增强粒子的多样性，继续寻优。

（4）

2 仿真实验

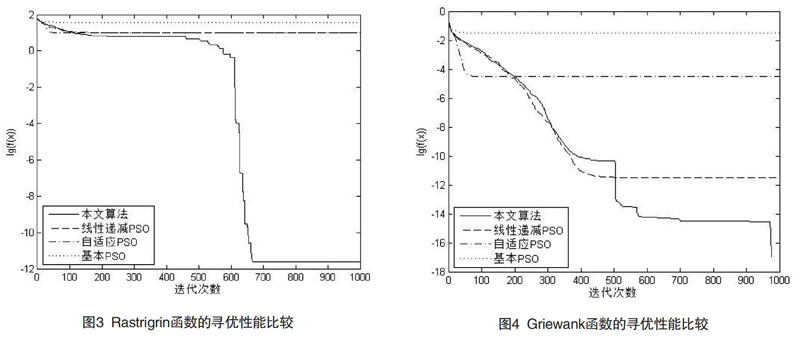
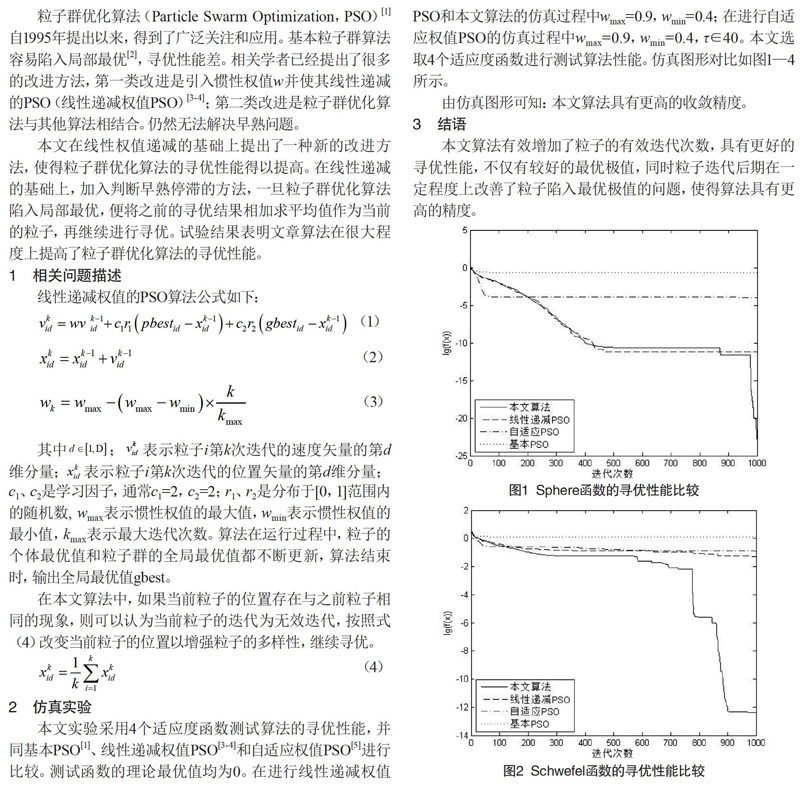
本文实验采用4个适应度函数测试算法的寻优性能，并同基本PSO[1]、线性递减权值PSO[3-4]和自适应权值PSO[5]进行比较。测试函数的理论最优值均为0。在进行线性递减权值PSO和本文算法的仿真过程中wmax=0.9，wmin=0.4；在进行自适应权值PSO的仿真过程中wmax=0.9，wmin=0.4，τ∈40。本文选取4个适应度函数进行测试算法性能。仿真图形对比如图1—4所示。

由仿真图形可知：本文算法具有更高的收敛精度。

3 结语

本文算法有效增加了粒子的有效迭代次数，具有更好的寻优性能，不仅有较好的最优极值，同时粒子迭代后期在一定程度上改善了粒子陷入最优极值的问题，使得算法具有更高的精度。

[参考文献]

[1]KENNEDY J，EBWEHART R. Particle swarm optimization[C].Honolulu：IEEE International Coference on Neural Networks，2002（8）：1942-1948.

[2]ANGELINE P J. Evolutionary optimization versus particle swarm optimization： philosophy and performance differences[C]. London：In Proceedings of the Seventh Annual Coference on Evolutionary Programming， 1998：601-610.

[3]SHI Y，EBERHART RC. Parameter selection in particle swarm optimization[C].Berlin： International Conference on Evolutionary Programming V II，1998（25）：591-600.

[4]SHI Y，EBERHART RC. Empirical study of particle swarm optimization[C]. Berlin：IEEE Congress on Evolution Computation，1999：1945-1950.

[5]安曉会，高岳林.混合变异算子的自适应粒子群优化算法[J].计算机应用，2008（6）：28-30.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。