《基于分形理论的灰度叶片图像压缩算法》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于分形理论的灰度叶片图像压缩算法

范文

金珊

摘要：植物叶片作为植物的重要特征，其图像的采集和传输具有重要意义。目前，图像压缩方法已有近百种，但压缩效果、压缩比及编码解码速度还不能满足叶片标本采录的特定要求。本文提出了基于分形理论的一种灰度叶片图像压缩的算法理论。利用叶片图像本身独特的几何特性对图像压缩方法进行改进，以求获得一种高压缩比，高分辨率的方法。

关键词：分形理论；叶片；图像压缩；拼贴理论；迭代函数

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2016）12-0185-03

1 叶片图像压缩现状

植物作为生态系统中最重要且基础的生产者，通过光合作用，植物调节空气中的碳氧比例，促进水及能量的循环流动，同时为人类提供了丰富的食物来源。植物为人类的生存与发展提供了广阔空间，为人类的生产生活提供了重要且丰富的物质基础。

面对日益增多的濒危物种，对物种保护工作的要求日益紧迫，植物分类研究是植物保护的一个重要方面。基于图像的描述方法弥补了传统的人工识别方法的不足，提高了植物识别工作的效率和准确性。快速、准确的识别方法对濒临植物物种的识别具有积极的作用，给植物保护工作带来了极大的便利。

1.1常规图像压缩方法

JPEG （Joint Picture Expert Group）是国际标准化组织（ISO）和CCITT 联合制定的静态图象的压缩编码标准。和相同图象质量的其它常用文件格式（如GIF，TIFF，PCX）相比，JPEG 是目前静态图像中压缩比最高的。

JPEG专家组开发了两种压缩算法、两种熵编码方法、四种编码解码方法。在实际静态图片压缩应用中，常使用的是有损的离散余弦变换（DCT）编码方法、Huffman编码和基于DCT的顺序编码方式，这一流程也称JPEG的基本方式。

1.2压缩原理（灰度、彩色）

1.2.1 颜色模式转换和采样

对于BMP图像，要将RGB颜色空间转换为YCbCr颜色空间（又称YUV颜色空间）。

其中人眼对亮度变换的敏感度远大于对颜色变换的敏感度，所以原本为Y：U：V=4：4：4的数据能够以Y：U：V=4：1：1或Y：U：V=4：2：2简化表示，前者称YUV411，后者称YUV422。

1.2.2 分块

由于DCT处理的是8×8的小块，在DCT处理前将图像分割成小块。图像中每点的信息由3个数据组成，将3个信息一次分离存放到3张表中。编码时，程序从源数据中依次读取和处理一个8×8的信息，然后是下一个。

若原始图像的长宽不是8的倍数，不能恰好分成8×8的小块，则补齐数据进行处理。

1.2.3 离散余弦变换（DCT）

DCT是码率压缩中常用的一种变换编码方法，它同傅里叶变换一样具有明确的物理意义，而数据量只有一半。对于渐变像素的图像，由于DCT使用的是半周期的基函数，变换效果反而好于。JPEG编码过程进行的是正向离散余弦变换，解码过程进行的是反向离散余弦变换。

这里的N是水平、垂直方向的像素数目，一般取值为8。经过DCT变换后得到8×8变换系数矩阵，有具体的物理意义。如，U=0，V=0时的F（0，0）是原来的64个数据的均值，称为直流分量（DC系数）；其他63个系数代表了水平空间频率和垂直空间频率分量的大小，多半是一些接近于0的正负浮点数，称为高频分量（AC系数）。变换后的系数矩阵中，低频分量集中在矩阵的左上角，高频分量则集中在右下角，这体现了DCT能量集中的特点。

1.3图像压缩指标

数据压缩方法的优劣主要有所能达到的压缩倍数、从压缩后的数据所能恢复（或称重建）的图像质量以及压缩和解压缩的速度等几方面来评价。此外，算法的复杂性和延时性也是应当考虑的因素。

1.3.1图像质量评估

图像质量评估包括主观评估和客观评估

1.3.2 JPEG压缩方法总结

采用JPEG标准可以得到不同压缩比的图像，在使图像质量得到保证的情况下，可以将每个像素24bit压缩到每个像素1bit。这一标准在速率上虽然效果很好，但在低比特速率的情况下，重构图像存在着严重的方块效应，不能很好地适应网络传输图像的要求。

2 从分形理论到分形图形学

2.1分形理论

1967年，Mandelbrot在《科学》杂志上发表了题为《英国的海岸线有多长？统计自相似和分数维度》（How Long Is the Coast of Britain？ Statistical Self-Similarity and Fractional Dimension）的著名论文。海岸线作为曲线，其特征是极不规则、极不光滑的，呈现极其蜿蜒复杂的变化。我们不能从形状和结构上区分这部分海岸与那部分海岸有什么本质的不同，这种几乎同样程度的不规则性和复杂性，说明海岸线在形貌上是自相似的，也就是局部形态和整体态的相似。

2.2用分形解决叶片模拟问题

根据叶片模拟的实现方法，可以将叶片图像的压缩视作模拟的逆过程，其中主要需要解决的问题是，如何高效率的寻找到”基本元”。或者说，作为一个逆问题，给出一幅图像，能不能找到一个混沌系统，使得已知的图像成为该混沌系统的吸引子？[3]

2.3迭代函数系统

迭代函数系统（Iterated Function System，IFS）提出了利用分形进行图像压缩的理论方法。IFS将待生成的图像看成是由许多与整体自相似的或经过一定变换与整体相似的（自仿射）小块拼贴而成。自相似性通过相似变换来实现，自放射性通过仿射变换来实现。

相似变换是指在各个方向上变换的比率必须相同的一种比例变换，仿射变换是指在不同的方向上变化的比率可以不同的一种比例变换。

2.4分形算法（sierpinski垫片）和原理

分形算法的典型例子是sierpinski垫片，sierpinski垫片可以看成是三角形△ABC被均分成4部分，然后将中间的三角形扣去，对其余三个小三角形重复操作。

2.5分形算法流程：

①生成随机数R，并使R的值在0与1之间；

②分配[ω1，ω2，ω3]，3个放射变换的概率空间平均分布于[0，1]；

③判断随机数落入哪一个概率空间，并调用相应的仿射变换所具有的的IFS码值，赋给相应的参数[ai，bi，ci，di，ei，fi]；

④根据放射变换的关系式，计算变换后的[x'，y']的值；

⑤在[（x'，y'）]处画一点；

⑥循环执行以上步骤，将上次计算变换后的值作为下一次的原位置值；

2.6不同的IFS码值产生不同的分形图

采用相同的放射变换的规则，但使用不同的放射变换系数会产生不同的图像结果。以前述sierpinski垫片为例，当第三个仿射变换的表达式系数依次为0.5，0，0.5时，会得到直角形的sierpinski垫片。

2.7一般图像的吸引子

分形算法在自相似图像的模拟、压缩和还原中的应用原理十分便捷，而简单的IFS系统只适合于具有高度自相似性的图像。但一幅一般的灰度图像（甚至彩色图像）需要的是更复杂的系统构造。

3分形叶的递归算法

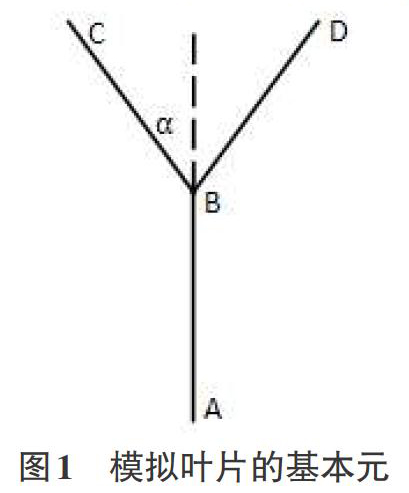
3.1基本元及原理

在叶片模拟中，可以以如图1的基本元为基本单位，利用递归算法不断进行迭代重画。

另外，改变构成分形叶的基本元的组成，也会影响最后的模拟效果。比如将基本元改成如图时构成的分形叶片很贴近自然树叶的形态。

3.3灰度叶片图像的算法

对sierpinski垫片进行压缩，仅需要存储3个仿射变换。实际图像上，这样“简洁”的图像比较少，仅通过几个压缩仿射变换就能够将自身变换到局部，但经验表明，实际图像中也存在局部的块与块的相似性。

3.4实现思想和流程

仿照普通图像压缩的方法，分形图像压缩的主要流程为：

①叶片特征参数提取：原图进行灰度处理，使亮度信息更明显；

②通过几何变换进行初步处理并记录几何变换信息。对图像进行平移、缩放、旋转（根据灰度图像的仿射变换，一般选择0°，90°，180°，270°旋转和垂直中线反射、水平中先反射以及对角反射）等操作，将叶片图像调整至合适的状态；

对比度和亮度信息可以利用最小二乘法得出。将原图像定义域块经过旋转反射和伸缩变换后的像素值与分割值域块的像素值按下式计算，最佳的对比度s和亮度o应使得R值最小。

③提取整体和局部具有自相似性的基本元（交叉线），确定位置和长度信息；

④判断各部分基本元落入哪个子块，并按相应的仿射变换所具有的的IFS码值，赋给必要的参数[ai，bi，ci等]；

⑤根据仿射变换的关系式，计算子块各个基本元所在位置的[x'，y']的值；

⑥将①②中的亮度、几何变换信息、④中的IFS码值进行编码。

4拓展

4.1分形图像压缩待解决的问题

分形图像压缩是有失真的，失真量大小与压缩比密切有相，尽管分形图像压缩有巨大的潜力，但要把这种潜力释放出来，还有许多问题有待进一步的研究，主要表面在：普遍性问题。对于一定的整体与局部存在明显相似性或仿射性的分形图像类，分形图像压缩方法的压缩比极高，但难以期望在很低的失真条件下，对一切分形图像压缩都具有极高的压缩比，只能在压缩比与失真度之间加以平衡。

4.2图像着色和彩色图像压缩

灰度图像与彩色图像相比，其细节存在许多差异，若将分形图像压缩方法应用于彩色图像，需要增加图像着色和还原的步骤。

自然界中，叶子之间存在颜色差异和互相遮挡，这表现为从树冠部分向下具有渐变的层次感。可以向IFS中引入概率集，用以控制落入相应拼贴子块的绿色点的数目。同时，添加随机干扰色彩，模糊色块之间的边界，使其呈现更好的颜色过渡。

参考文献：

[1] 姚宇飞.基于分形维数的叶片识别方法研究[D].北京：北京林业大学，2011.

[2] 滕姿.基于分形的图像压缩研究[D].西南大学，2008.

[3] 曾曲文，文有为，孙炜.分形、小波与图像压缩[M].沈阳：东北大学出版社，2002（10）：97-98；105-109.

[4] 孙博文.分形算法与程序设计：Visual C++实现[M].北京：科学出版社，2004（11）：52-54.

[5] 柳青松.分形图像压缩[J].火控雷达技术，2002（31）：61.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。