《基于偏好的有向图的路径搜索问题的研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于偏好的有向图的路径搜索问题的研究

范文

赵晓东　陈思宇　方欢

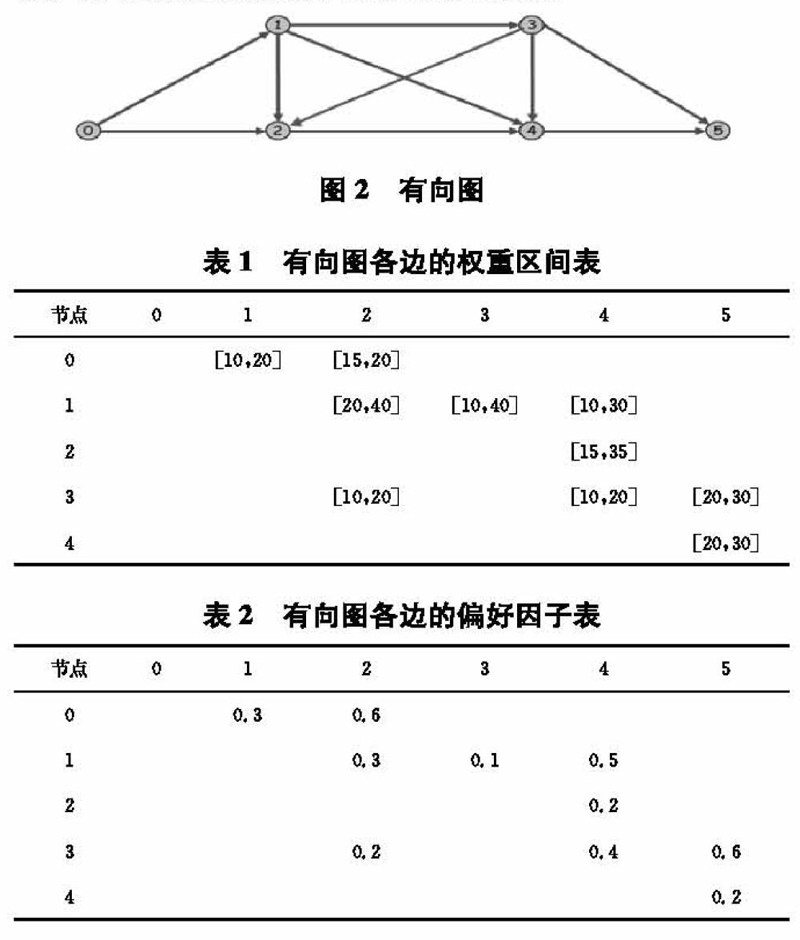
摘要：目前，路径搜索问题在生活中的很多领域都能得到应用。生活中存在很多可转化为如下表述的实际问题：有向图图中边的权值是一个区间[a，b]，其中a表示最小代价b表示最大代价，根据个人偏好给出各边的偏好因子和一个目标值F，找出从源点到汇点的所有路径中，满足边的偏好权重值之和

关键词：有向图；偏好；路径搜索；深度优先；路径优化

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2017）07-0192-03

1背景

路径搜索问题在很多领域都有其研究的价值，很多问题最终都可以转化为图的路径搜索问题。常见的路径搜索算法有：Dijkstra算法、BSF算法、A*算法等。Dijkstra算法是通过中心为起点，以辐射状不断向中心外搜索（每次取距离起点最近的点），一圈一圈向外扩张，直到逼近目标点，完成路径搜索，它较能适应网络拓扑的变化、性能较稳定等；BSF算法每次扩张节点，都是通过启发函数选择最接近目标的节点，最终完成搜索；A*算法兼具Dijkstra准确和BSF的快速，在搜索路径时，通过启发式函数计算当前节点到目标节点的距离，而起始点到当前点距离已知，则每次选择初始点到目标点的代价估计最小的节点，A*算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。A*算法中的距离估算值与实际值越接近，最终搜索速度越快。以上算法都是用来求解最短路径搜索问题，大多数研究者也都是对最短路径搜索问题在不同领域进行研究。

在实际生活中，人们往往会遇到做一件事情的代价在一定范围内波动的问题，将这种问题转化为图的问题进行解决，即是图中边上的权值在一定区间范围内，于是引入权重区间来表示图中边的权的取值范围。对于同一件事情有不同的解决方法，由于各种因素导致对于不同的方法有着不同的倾向，于是将问题转化为图的问题后引入偏好因子用来衡量个人对边的倾向程度，表示对该边的倾向占整体的比例。实际问题中由于某些因素的限制，会使得问题的处理具有一定的局限性，即便问题的处理具有多样性，但是还是需要根据实际来选择解决的方法，将这种问题转化为图的问题引入偏好权重来表示解决问题的方法中根据代价的范围以及倾向程度决定的带入计算的具体的值。通过改进深度优先搜索算法，根据各边的偏好因子和权重区间确定偏好权重，在有向图环境下搜索出所有满足目标值条件的路径，并很容易得到最短路徑。

2改进的深度优先路径搜索方法

2.1深度优先搜索{DFS}

假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点（源点），则深度优先搜索可定义如下；首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点（亦称为从源点可达的顶点）均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。算法流程如图1所示。

2.2改进的深度优先搜索及具体求解过程

由于采用深度优先搜索只能得到一条路径，为了解决上述问题得到所有满足条件的路径，于是对深度优先搜索做如下修改。

设x是当前被访问顶点，在对x做过访问标记后，选择一条从x出发的未检测过的边（x，y）。若发现顶点y已访问过，则重新选择另一条从x出发的未检测过的边，否则沿边（x，y）到达未曾访问过的y，对y访问并将其标记为已访问过；然后从y开始搜索，直到搜索完从y出发的所有路径，即访问完所有从y出发可达的顶点之后，才回溯到顶点x，并且再选择一条从x出发的未检测过的边。上述过程直至从x出发的所有边都已检测过为止。此时，若x不是源点，则回溯到在x之前被访问过的顶点；否则图中所有和源点有路径相通的顶点（即从源点可达的所有顶点）都已被访问过，若图G是连通图，则遍历过程结束，否则继续选择一个尚未被访问的顶点作为新源点，进行新的搜索过程。

满足目标值的搜索算法的伪代码如下所示：

访问顶点V0；visited[V0]=1；

W=顶点V0的第一个邻接点；

While（W存在）{

if（W未被访问and W非栈顶结点）从顶点W出发进行深度优先搜索；

else（W为栈顶结点）

弹出栈计算路径偏好权重；

if（符合目标值）输出路径及总代价

else舍弃路径

W=顶点V0的下一个邻接点；

}

下面将通过一个具体的例子来说明满足目标值的搜索过程。有向图相关数据见图2、表1、表2所示。

根据各边的偏好因子以及权重区间得到各边的偏好权重，如表3所示，偏好权重的计算方式如下：

假设边的权重区间为[a，6]，边的偏好因子为d，则边的偏好权重w为：

当偏好因子的取值范围为0-1时，偏好权重取值范围为a-6。

根据图1所示的有向图以及表1、表2、表3，求解节点0到节点5的满足目标值的所有路径的实现过程如图3所示。图3所有路径求解的实现过程图

3结果及分析

当目标值为70时，利用改进的深度优先搜索算法根据上述数据运行得到结果如下：

当前的顶点个数是：6

目标值为：70

第V0个节点；V0-V0：0 V0-V1：1 V0-V2：1 V0-V3：0 V0-V4：0 V0-V5：0

第V1个节点：V1-V0：0 V1-V1：0 V1-V2：1 V1-V3：1 V1-V4：1 V1-V5：O

第V2个节点：V2-V0：0 V2-V1：0 V2-V2：0 V2-V3：0 V2-V4：1 V2-V5：0

第V3个节点：V3-V0：0 V3-V1；0 V3-V2：1 V3-V3：0 V3-V4：1 V3-V5：1

第V4个节点：V4-V0：0 V4-V1：0 V4-V2：0 V4-V3：0 V4-V4：0 V4-V5：1

第V5个节点：V5-V0：0 VS-V1：0 V5-V2：0 V5-V3：0 VS-V4：0 VS-V5：0

其中0表示两个相邻顶点之间不存在通路，1表示两个相邻顶点之间存在通路。

V0->V1->V3->V4->V5总代价为：62.0

V0——>V1——>V3——>V5总代价为：52.0

V0——>V1——>V4——>V5总代价为；55.0

V0——>V2——>V4——>V5总代价为；59.0

由上述结果可知，满足条件的路径共有4条，并且很容易得到最短路径为V0->V1->V3->V5->总代价为：52.0。重复上述实验，随着目标值的增大，满足条件的路径数目也越来越多。

4结束语

在满足给定条件下，根据个人偏好和目标值采用改进的深度优先搜索方法，实现了给定条件下带权有向图的路径搜索。通过各边的偏好因子和权重区间确定偏好权重，利用栈结构保存从起始顶点到目标顶点在限制条件下的路径顶点，从而完成限制条件下满足个人偏好的路径搜索。在本文的基础上也很容易将算法推广到限制条件下满足个人偏好的无向图的路径搜索。本算法的优点是能够人性化的结合每个人的不同偏好，在限定条件下对有向图进行路径搜索。本文限制条件下满足个人偏好的有向图的路径搜索可以用来解决房子装修问题、交通线路选择问题等方面。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。