《联结经验：创新背景下统计学教学的一点思考》-理学论文，数学论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

联结经验：创新背景下统计学教学的一点思考

范文

陈玲菊谢碧华

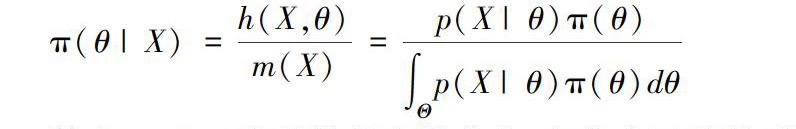
【摘要】在大数据时代，统计学与多学科的相互渗透使得传统的简单性教学原则的局限性逐渐显现出来.本文是在法国当代思想家埃德加·莫兰（Edgar Morin）所提倡的复杂性科学视野下，讨论用联结经验的方法进行统计学教学的一点思考.

【关键词】统计;创新;联结;经验;脑科学

【基金项目】福建省中青年教师教育和科研项目.基金号：JAT160383.

一、引言

如何在课堂上行之有效的教学？从美国心理学家约翰·华生（John Broadus Watson）创立了行为主义学习理论以来，在格思里、赫尔、斯金纳等的影响下，行为主义学习理论在美国占据主导地位长达半个世纪之久.行为主义者认为，学习是刺激与反应之间的联结，他们的基本假设是：行为是学习者对环境刺激所做出的反应.他们把环境看成刺激，把伴随的有机体行为看作反应，认为所有行为都是习得的.行为主义学习理论应用在学校教育实践上，就是要求教师掌握塑造和矫正学生行为的方法，在最大限度上强化学生的合适行为，消除不合适行为.对教育而言，这种建立在刺激与反应联结上的教学模式，只强调外部刺激而完全忽视学习者的内部心理过程，忽略了人脑的认知行为与动物的区别，训练虽然可以调整人的行为反应，但却忽略了人们对未来意外事件的理解力.随着脑科学中有关人的高级认知机制研究成果的呈现及人们对学习本质的认识的不断深入，以创设网络式联结为导向、基于情境学习和情境认知的理论研究和实践模式的开发越来越受到心理学、人工智能、人类学等领域研究者的关注.

脑研究表明人的大脑是个并行处理器.在学习中，人脑会对有意义和无意义的信息与场景做出不同的反应.仅存在于记忆中的事实没有意义，但当事实与复杂却熟悉的经验联系起来时就产生了意义，这样，新的信息就与我们已经知道和掌握的信息联系在一起了.人脑复杂的模式化核心特征对教学提出：优秀的教师不只是为测试而教.而是会利用学生带到班上的背景和信息来展开教学，这些背景与信息包括他们与家长的经验、力量和爱.在学习过程中，学生能更好地领悟他们自己和生活，浸润在学科当中，其经验的拓展和心理的升华也随之开始.对于统计学这门与人们的日常生活息息相关的学科，如何在教学中利用联结将统计的方法和思想“编排”到学生对已有客观世界的体验中？如何恰如其分地结合一些实验和例子将统计学内化为世界观和方法论？如何培养学生运用统计学的思想方法发现问题、分析问题和解决问题的能力？这是当今社会对创新人才日益高涨的需求下，每一位任课教师所要思考的问题.

传统的数学教学方法，往往只满足于对定理、公式的陈述與证明，以及对技巧的应用，照搬课本内容.这样容易造成数学孤立于生活经验，与现实失去联结，完全变成了冰冷冷的教条.这种教学实际上是过分强调记忆——对定义、公式和定理或者是对解题技巧的记忆.在这种教学方式下，学生失去了主体地位，只是被动地吸收、消化，学习兴趣不高，没有积极性，更谈不上知识的创新与运用.关于统计的教学方法，已经有很多讨论，比如案例教学、“辨误”教学、启发教学、讨论教学，这些方法为统计教学的改革和创新提供了宝贵的参考.但是鲜有具体讨论如何利用联结进行创新性教学的尝试.事实上，从约翰·格兰特（John Graunt）清点伦敦的死亡人数，建立人类历史上第一张死亡表开始，统计的方法与理论就在为人们提供便利，并在解决生活中的实际问题中不断发展.教材中所呈现的定义、公式和定理是众学者在几百年来对客观世界的观察、体验的基础上抽象出来的套装知识，每个定义、公式和定理都有其产生背景及在现实中的应用.因此，改进教学方法的首要任务就是设计编排课堂的教学内容.教学不仅要讲定义、公式、定理，还要适当地引入背景知识，从而将教材中的套装知识与学生的主体经验联结在一起，尽可能地将教材中冰冷冷的知识骨架转化为有血有肉的、被学生所喜闻乐见的形象.这样能够激起学生的兴趣，并为进一步引导学生运用统计的思想方法去发现、思考、解决身边或社会上的问题打下基础.接下来，结合多年教学实践，笔者总结了教学中常用的几个例子，希望为广大同仁提供参考借鉴.

二、案例

首先，统计有什么用？我们可以引入一个古老的寓言故事：在非洲草原上如果见到羚羊在奔跑，那一定是狮子来了;如果见到狮子在躲避，那就是象群发怒了;如果见到成百上千的狮子和大象集体逃命的壮观景象，那是——蚂蚁军团来了！

这个寓言实际上就蕴含着统计推理的基本过程：观察现象——做出推断.统计中的观察是通过试验收集和分析数据（观察现象），从而对研究对象的客观规律做出合理的估计和判断.

1.随机抽样

随机抽样在日常生活中随处可见，如看看饺子是否煮熟了，就随便捞一个尝尝，这就是随机抽样.在随机抽样中，样本的抽取要满足随机性，否则，将影响试验结果的客观性，从而导致试验失败.比如美国的盖洛普民意调查机构，其创始人乔治·盖洛普在1932年成功地预测出其岳母将在州政府秘书的竞选中获胜.接着在1936年及其后的两次总统选举中都正确地预测出获胜的一方.但是在1948年的总统选举中，对谁将接任罗斯福成为下一任总统时，基于50000人次的调查，预测杜威获胜.但实际结果是杜鲁门获胜.民意测验出了什么问题？真实情况是，1948年的民意调查访问人员选择了过多的共和党人.这是因为共和党人较为富裕，受过较好的教育，住在较好的街区，较易接受访问，所以访问人员喜欢采访共和党人，这就造成了民意测验中偏向共和党的现象.

现在，盖洛普民意测验仍然享誉全球.在盖洛普民意测验中出现非常频繁的问题有：谁是最受人们赞美的人？男人是否会选择健康又美丽的女人？而盖洛普民意测验中最热门的十大问题是：为什么人生在世会有患难？是否有一种方法可以医治所有的疾病？世界上为什么有罪恶的存在？人类会迎来永久的和平吗？人与人之间会彼此相爱吗？世界末日何时来临？我和自己的家庭能有什么样的未来？人死后还有生命吗？天国会是什么样子？我怎样才能成为一个更加淳朴高尚的人？

抽样调查问题的核心便是抽样，抽样的原理很简单，但是很多“谎言”就是出自看似简单的抽样.比如曾经在美国的《时代周刊》上有这么一条信息：1924级的耶鲁毕业生平均年收入有25111美元.这在当时可是绝对的高收入了.那么，我们是马上惊呼耶鲁毕业生真棒，还是应该质疑一下它的真实性呢？它的调查样本是什么？经过了半个世纪他们能找到所有1924级的耶鲁毕业生吗？或许只是用了抽样调查.那么它的这个抽样调查是真的具有代表性吗？它能联系到的只是那些功成名就的畢业生吧，那些在毕业生通讯录上被注明“地址不详”的迷路小羔羊呢？就算它的抽样具有一定的代表性，那么所有接受调查的毕业生，说的都是真话吗？会不会因为虚荣或是逃税而说假话？即便这所有都是真的，那么这个收入平均数的类型是什么？是均数、中位数还是众数？

在数据泛滥的时代，真实的信息与噪音同时存在，我们要学会运用统计学的思想方法进行分析思考，去伪存真，分辨出其中隐藏的谬误之处，从而更加客观地认识我们所处的世界.再比如“辛普森悖论”：英国统计学家辛普森（E.H.Simpson）在1951年发表的论文中指出，在某些情况下，在分组比较中占优势的一方，可能在合并后的总评中成为失势的一方.比如：1991年美国航空协会收集阿拉斯加航空和西美航空飞经5个机场的误点数据如下表.

阿拉斯加航空在所有5个机场都更为准点，但总体上却是西美航空公司更为准点！类似的问题还可能出现在学校招生比例、职场的录取率等问题中.辛普森悖论被人们称为是“投向统计学的炸弹”，无可挑剔却让人难以接受.然而探究其数学实质，不难发现，其诡异的外表下，内部却十分简单：

分数ba>fe，dc>hg，但分数b+da+c未必大于f+he+g.

这就告诉我们对于总体现象，要仔细研究细节，不要轻易下结论.

2.假设检验思想与贝叶斯理论

假设检验的基本思想是依据概率论中的小概率原理，应用概率反证法，通过观察小概率事件是否发生来判别关于总体的假设是否正确.小概率的事件在一次试验中几乎不可能发生，如果真的发生了，那么我们就认为原假设值得怀疑.关于这个思想可以引入一个古代的故事：

魏晋名士王戎七岁的时候，曾经和其他小朋友一起出去玩，路边一棵李子树上结满了李子，多到把树枝都压弯了.许多小朋友争相跑去摘李子，只有王戎不动.有人问他为什么，他说：“这李子树就长在路边却结了那么多果实，其果实必定是苦的.”后来别人摘来果实一尝，果然如此.

在这个故事中，王戎就引用了概率反证法.假设路边的李子是甜的，那么树上有这么多李子应该是小概率事件，既然小概率事件发生了（即李子多到把树枝都压弯了），那么就怀疑原假设，即认为李子是苦的.

统计中的假设检验利用的就是概率反证法.关于假设检验的方法，《女士品茶》一书中有这样的例子：在英国剑桥一个夏日的午后，一群大学的绅士和他们的夫人们，还有来访者，正围坐在户外的桌旁，享用着下午茶.在品茶过程中，一位女士说：“奶茶是先放红茶还是先放牛奶，味道完全不一样，我一下子就能品尝出来”.在场的一帮科学精英们对这位女士的“胡言乱语”嗤之以鼻.这怎么可能呢？他们不能想象，仅仅因为加茶加奶的先后顺序不同，茶就会发生不同的化学反应吗？然而，这个问题引起了在座的一位先生的兴趣.他提议做一项试验来检验如下假设是否可以接受.

假设：该女士无此种鉴别能力.

他在女士看不到的地方准备了10杯分别利用两种方法冲泡的奶茶.结果那位女士竟然正确地分辨出每一杯的冲泡顺序，那么我们是否拒绝假设呢？这位先生的想法是：如果假设是真的.那么，每次猜对的概率都是0.5，10次都猜对的概率是2-10，显然是小概率.小概率事件发生了，于是拒绝原假设，即认为该女士有此种鉴别能力.

在生活中，对小概率问题人们一般不会担心.“杞人忧天”就是将普遍共识是小概率的事件的概率放大的结果.实际上，由于每个人都有自己的信仰和偏见，所以对事件发生的概率的估计各不相同，这些估计与客观概率的差距大小不一.贝叶斯理论告诉我们，尽管我们的信念使我们对事件的预测永远做不到完全客观、合理或是准确.不过，我们可以不断收集证据，一步步调整对事件的预测，使之一步步靠近事件的真相.我们可以简要地描述一下贝叶斯理论：对于事件A，假设我们原来认为它发生的概率为P（A），如果我们观察到事件B，那么在事件B的基础上，我们可以将事件A发生的概率调整为：

P（A|B）=P（B|A）P（A）P（B|A）P（A）+P（B|A）P（A）

其中，P（B|A）为在事件A发生的条件下事件B发生的概率，P（B|A）为在事件A没发生的条件下事件B发生的概率.一般地，我们称P（A）为先验概率，而在事件B基础上调整得到的概率P（A|B）为后验概率.

实际上，贝叶斯理论当初是用来表达贝叶斯的哲学观：上帝是完美的，他创造自然是有章可循的，我们可以通过近似值一点点地模拟并认识宇宙.收集的证据越多，就越接近真相.贝叶斯的朋友在向众人呈现《机会的学说概论》时举了一个“人”的例子：作为第一个出现在这个世界的人，第一次看见日出时并不知道日出是必然还是偶然现象.然而随着日后每一天的日出，他信心一步步增强，直到最后他预测每天太阳升起的概率是100%.

再比如美国的“9.11”恐怖袭击事件.2001年9月11日清晨，当人们从梦中醒来时，大部分人都想不到恐怖分子的飞机会撞向曼哈顿世贸中心大楼.但是，世贸中心第一次遭受袭击后，人们才意识到这也许是一次恐怖袭击.直到第二座高楼被袭击之后，人们才相信确实遭遇了恐怖袭击.

贝叶斯定理可以解释这一过程.比如，在第一架飞机撞击大楼之前，我们预测曼哈顿的高楼遭遇飞机撞击的概率只有1：20000或0.005%.当然，我们还是会认为世贸中心意外遭遇飞机撞击的概率是非常低的.人们靠经验也能准确地预测出0.005%这个数字：9月11日之前的25000天，虽然一直有飞机盘旋在曼哈顿的上空，但是只发生了两次这样的意外事故：一次是1945年的美国帝国大厦事件，另一次是1946年的川普大厦事件.这样看来，此类意外事故发生的概率只有1∶12500.在第一架飞机撞上世贸中心大楼的那一刻，用贝叶斯定理计算（见表），发生飞机撞击事件的概率便会从0.005%剧增致38%.

接下来，我们看看第二次袭击发生之后，由贝叶斯定理得到的遭遇袭击的概率会变为多少.这次，38%是先验概率.这时根据贝叶斯定理得到的遭遇恐怖袭击的概率就变成了99.99%，这就表示恐怖袭击一定会发生！

先验概率恐怖分子架机撞击曼哈顿世贸中心大楼的初始概率预估P（A）38%

美国的乌尔加利斯作为当今世界顶级的赌徒就是成功利用贝叶斯定理的一个很好的范例.他特别喜欢看NBA比赛并投注.每年从11月至下一年6月，乌尔加利斯每晚都会观看NBA，每次看5场，分别由5台电视机同时播放.事实上，几乎所有的NBA比赛他都看过——不论是直播还是录播.除此之外，他还经营着一家球探服务机构（本质上来说其实是为他自己服务的），雇用了一些助手，让这些助手将每个球员在每场比赛中的防守阵形绘制成图，这种做法给乌尔加利斯带来的好处就连很多NBA球队都望尘莫及.他关注了几十名球员的微博，仔细查看每140个字符的微博内容，试图从中找出关联信息：若某位球员在微博上说自己那晚晚些时候会去某个夜总会，则这位球员的心思很可能根本就没在比赛上.他也很关注球队教练在新闻发布会上说的话，比如，如果某位教练说，他希望他的队伍“学习进攻”或者“练好篮球基本功”，那可能表明他希望放慢比赛的节奏.

乌尔加利斯靠着这些小秘密，即使年景比较差的时候也能赚上100万美元，年景好的时候，可以赚上三四百万美元.他的成功就是建立在贝叶斯思维上的，不断寻找证据，那么你的预测会越来越接近客观现实.这种思想反映在参数估计里，就形成了贝叶斯估计方法：在已知总体分布的情况下，贝叶斯学派认为待估参数θ可以看作随机变量，在得到新的样本信息之前，人们对θ的认知是先验分布π（θ），在得到新的样本信息X后，人们对θ的认知为π（θ|X），称为后验分布，它的计算公式是：

π（θ|X）=h（X，θ）m（X）=p（X|θ）π（θ）∫Θp（X|θ）π（θ）dθ

其中p（X|θ）为总体的条件分布，它集中了总体、样本和先验中有关θ的一切信息.其计算公式就是用密度函数表示的贝叶斯公式.由此得到的后验分布π（θ|X）是用总体和样本对先验分布做出的调整方法，要比π（θ）更接近θ的实际情况.

综合起来看，则好比是人类刚开始时对大自然只有少得可怜的先验知识，但随着不断的观察、实验获得更多的样本、结果，人们对自然界的规律摸得越来越透彻.所以，贝叶斯方法既符合人们日常生活的思考方式，也符合人们认识自然的规律，因而经过不断的发展，最终占据统计学领域的半壁江山，与经典统计学分庭抗礼.

法国当代思想家埃德加·莫兰（Edgar Morin）写的《未来教育所必需的七种知识》指出，教育的一个黑洞就是人们教授确定性，然而需要教授的恰恰是不确定性.今天，所有伟大的科学，从微观物理学到人类进化学都成为确定性和不确定性之间的赌博.在所有领域，特别是人类历史领域，必须讲授出人意料的事情.“在这个昏暗的世界，我们被迫在充满不确定因素的海洋上航行，时而穿行于确定的群岛之间，这就是人类的冒险.今天，我们知道这是未知的冒险，我们需要一种教育，能帮助我们面对这个冒险而不气馁”.

总之，统计不仅是一种重要的“方法”或“工具”，也是一种思维模式;不仅是一门专业学科，也是一种文化;不仅是一些知识，更是一个人的文化素质.在充斥着各种各样的信息与噪音的大数据海洋中，对统计学的正确使用可以帮助我们在各种冒险中获得创新与创业的先机.

【参考文献】

[1]雷纳特·N.凯恩，杰弗里·凯恩.创设联结：教学与人脑[M].吕梅海，译.上海：华东师范大学出版社，2004.

[2]赵焕光，章勤琼，王迪.真理相遇统计[M].北京：科学出版社，2019.

[3]朱辰辰.关于《信号与噪音》的翻译实践报告[D].天津：天津师范大学，2014.

[4]茆诗松，周纪芗.概率论与数理统计：第二版[M].北京：高等教育出版社，2000.

[5]达莱尔·哈夫.统计陷阱[M].廖颖林，译.上海：上海财经大学出版社，2002.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。