《泛集群环境下联盟体形成方法研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

泛集群环境下联盟体形成方法研究

范文

丛峰刘瑞超

摘要：在采用智能体结盟的方式解决多目标约束下的合作计算调度问题通时，提出了一种提高联盟体形成效率和可靠性的方法。首先，为定量化描述联盟体的优劣性，将谈判集约束条件和联盟基本理性期望作为适应度函数;其次，引入莱维飞行粒子群算法求解最优联盟体结构，以保证求解速度和最优解质量;最后，通过算法性能测试验证了方法在求解效率和可靠性方面具有明显改善。

关键词：泛集群;协同调度;联盟体;博弈算法;莱维飞行粒子群算法

中图分类号：TP273? ? ? ? 文献标志码：A

文章编号：1009-3044（2019）23-0195-05

开放科学（资源服务）标识码（OSID）：

A Method for Coalition Structure Generation Under the Generalized-Cluster Environment

CONG Feng， LIU Rui-chao

（Daqing Oil Company Exploration & Development Research Institute， Daqing 163000， China）

Abstract： The scheduling problem under multi-objective constraint is usually solved using the agent coalition. In this paper， a method to improve the efficiency and reliability of the coalition structure is presented. First， to improve the solving speed and the optimal solution quality， the constraint conditions of the bargaining set and the coalition's basic rational expectation are taken as the fitness function. Second， the particle swarm optimization algorithm based on Levy flight is introduced to solve the optimal coalition structure. Finally， the availability of the method in solving efficiency and reliability is verified according to the experiment simulation and test in terms of convergence， effective rejection rate， algorithm performance and other aspects.

Key words： Generalized-Cluster; co-allocating scheduling; cooperation game; Coalition Structure; Levy-flight PSO

1 背景

泛联盟是一组为完成特定任务而形成的泛集群集合，它为泛集群解决大规模科学计算问题提供了一种重要的合作方式[1]。作为一个动态性的概念，泛联盟随着新任务的到来而产生，又随着任务的完成而解体。有关泛联盟形成的研究本质是解决智能体自组织机制设计问题，科研人员热衷于采用启发式最优解算法和合作博弈理论等方式解决這一问题，尤其是在多任务多目标约束的条件下如何求解最优泛联盟结构（联盟体）。

采用启发式最优解算法的基本思想是枚举全部可能得到的联盟体，通过编码等方式转换为可描述的对象，并由全局或局部最优解快速算法获取最好的泛联盟结构。Ali.M等[2]提出了一种高效的差分进化算法求解多目标约束的最优配置问题，虽然计算速度快、收敛性强，但在解决多目标约束的离散点问题时，最优解的质量无法保证;Zhao Q和Zhang L Y [3]研究了离散粒子群算法（DPSO）在团队选择优化中的应用，由于考虑了离散点的局部聚集问题使得求解质量更高，但应对大量离散点时候体现出算法自身的不稳定性;张国富[4-7]近年来一直深入这一领域的研究，并在求解重叠联盟、最大成功联盟等问题上成果颇丰，但解决泛集群成员稳定性的能力相对不强。

为解决上述问题，引入并改进莱维飞行粒子群算法[8] （Levy-flight PSO，L-PSO）以提高求解的质量和稳定性。第二部分阐述了基础工作并提出需要解决的核心问题;第三部分讨论了基于L-PSO的最优联盟体求解过程;第四部分通过收敛性测试、性能分析、剔除率测试等实验证明了方法在求解的效率和质量方面具有明显改善;第五部分总结研究成果。

2 基础工作

构建生态场景：非超可加环境H由泛集群集合[Sn]构成，[Tm]表示一组大规模科学计算任务，[Tm]将由多个泛集群以联盟形式完成，记作[Umk=N，v]。这一场景需要三个前提：1）允许[m=1];2）[Sn]在某一时刻或阶段内只能参与一个泛联盟，即仅存在完全参与或完全不参状态; 3）[Tm]是可并发的。[Umk]在完成任务后将获得一定的效用[vmUmk]，[vmUmk]的特征函数可表示为公式（1）形式。

[vmUmk=pTm-cUmk-eUmk]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1）

[Umk]的性价比[bmUmk=vmUmk/tmk]，在此反应了泛集群的个体理性为期望性价比最高，如公式（2）所示，其中[tmk]表示[Umk]完成[Tm]的预期完成时间。

[fx=argmaxbmUmkbmUmk=pTm-cUmk-eUmk/tmk]? ? ? ? （2）

定义表示[Umk]在完成[Tm]中所能获得的最大效用值（也成为联盟值[14，16]），即。更新公式（2）得到个体理性期望如公式（3）描述。

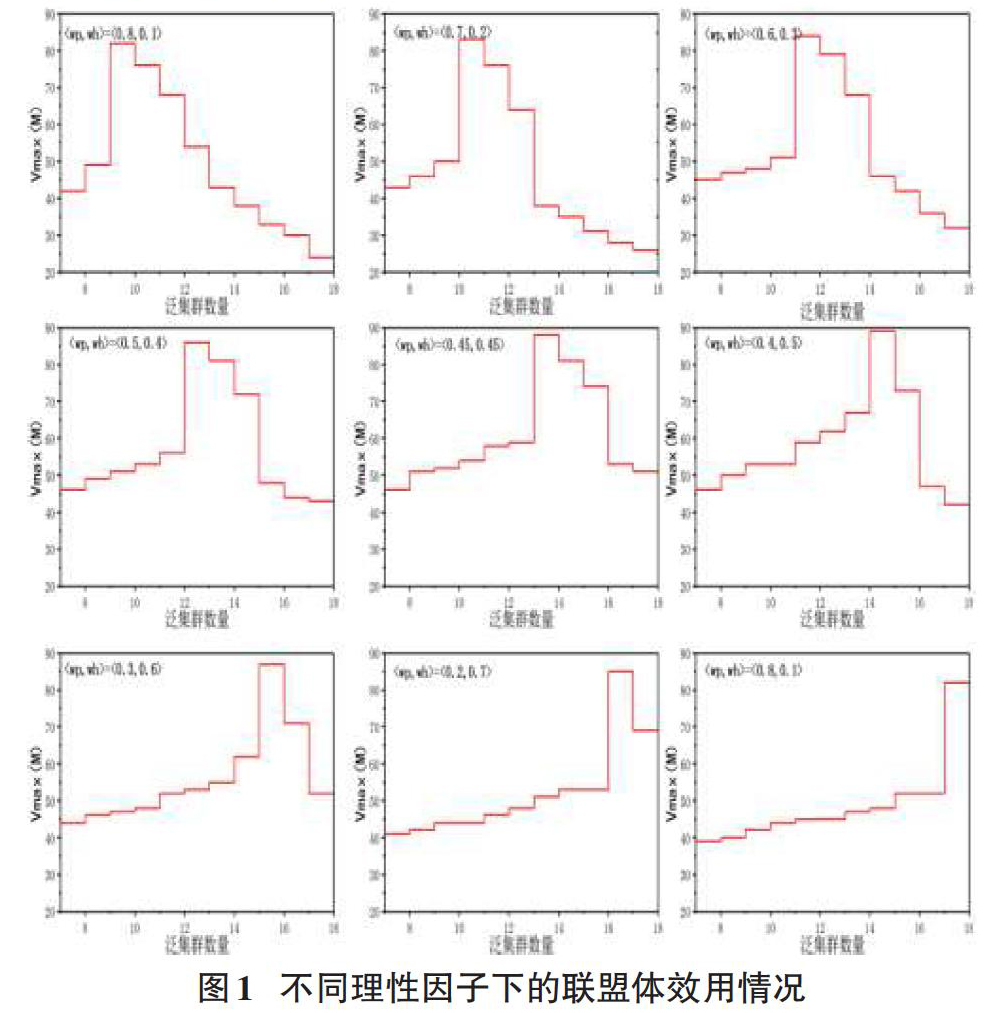
[fx=argmaxbUmkbUmk=maxo

定义1.根据Branzei等[9]关于合作博弈模型的描述可知，联盟体由若干个泛联盟构成，每个泛联盟负责完成一个任务，联盟体[M]要求满足公式（4）描述。

[?M=U1…UdUi?Ut=?，i≠t，Ui，Ut∈UdUdc=1Uc=R]? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

所有可能形成的聯盟体集合表示为[Ms]，定义[xs=x1s，x2s…xns]表示由[Ms]的所有成员获得的效用构成的一个分配向量。已知联盟体必然满足集体理性，具体表现为：1）所有效用需分配给所有的泛集群成员（如公式（5）所示）;2）联盟体总是期望总支出[om]最少（如公式（6）所示）。

[xs=pTm-cUmk]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（5）

[argminomk，omk=cUmk+eUmk]? ? ? ? ? ? ? ? ? ? ? ? ? （6）

在泛集群环境下，[vmUmk]为非超可加的[2]，理论可形成的泛联盟数量为[count=2n]。

由合作博弈理论可知，联盟体的基本理性期望要求同时满足个体理性和集体理性[10]。根据公式（3）、（5）、（6）给出联盟基本理性期望可描述为公式（7）形式。

[Rb=pm，k=fxgm，k=∑pTm-cUmkhm，k=argmincUmk+eUmk]? ? ? ? ? ? ?（7）

为描述成员（泛集群）的倾向意图，引入理性因子[ωRb=ωp，ωg，ωh]，[ωp+ωg+ωh=1]作为衡量理性期望的指标，定义阈值[?]，给出基本理性期望函数如公式（8）所示。

[fRb=ωp×pm，k+ωg×gm，k+ωh×hm，k]? ? ? ? ?（8）

泛联盟既定所有的效用均分配给所有成员，为降低[ωg]的影响，设定[ωg=0.1]。[ωp，ωh]分别表达了联盟体的主观意愿，根据公式（2）可知：[ωp]体现了个体理性，当[ωp]变大时，个体成本支出将降低，但是联盟合作支出将提高，即[ωp↑→cUmk↓，eUmk↑];[ωh]反应了联盟理性，当[ωh]变大时，个体成本支出将提高，但是联盟合作支出将降低，即[ωh↑→cUmk↑，eUmk↓]。效用分配向量直接反应泛集群的意图，并将决定联盟体结构。因此，如何快速准确的求解最稳定分配向量问题是需要解决的核心问题之一。

3 最稳定联盟体的选择

3.1 问题的转化

最稳定分配向量决定最终的联盟体结构。将谈判集约束作为最优联盟求解的适应性函数，从场景[H]的角度给出定义2。

定义2.定义合作博弈[GSn，vU]的分配向量[x=IvSmk，U]，任意成员[Sc，Sι∈U]。 [Sc]对[Sι]的异议可表示为[Pιc，y]，其中[Pιc]表示一组泛联盟，[Sc?Pιc，Sι∈Pιc]。于是[Pιc]的分配向量[y]必然满足：[yPιc=vPιc，yi>xi，i∈Pιc]。[Pιc，y]的反异议可表示为[Pιz，z]，[Sl?Pιz，Sc∈Pιz]，于是[Pιz]的分配向量[z]必然满足：[zPιz=vPιz，zi>yi，zj>xj，i∈Pιc?Pιz，j∈Pιc＼Pιz]。

如果[?Pιc→Pιz=?]，则表示[Sc]对[Sι]的任何异议都不存在反异议，记做[Sc?nxSι]。因此合作博弈G[Sn，vU，M]的Mas-Colell谈判集为如下集合：[MC=Sc?nxSι，MC∈U]。

[MC]的求解使泛联盟的基数[?2n]，对[MC]的所有成员进行降序排列，搜索可以覆盖全部成员的联盟组合，取其成员密度最高的[h]项即构成[Ms]。因此问题2可以描述为以[Ms]为样本，求分配向量[xs]的似然最优解问题，等价于求解效用最高的联盟结构体（即[vmaxMs]）的问题。

对问题进一步描述：取谈判基础联盟[Smk]，根据公式（1）可知[xs=p-e+c]，[p]恒定，于是求解[vmaxMs]等价于求解期望[maxxs≡minm1em，k+cm，k]。根据公式（2）引入高性价比因子，得到距离公式[disc，e=em，k/tmk+cm，k/tmk]。

[xs]可由[em，k，cm，k]表示为

[xs=e11+c11…em1+cm1???e1k+c1k…ekk+ckk]

以[em，k，cm，k]分别表示[xs]的空间位置。令[em，k>1，cm，k>1]，由公式（7）、公式（8）给出目标函数如公式（12）所示。

[fRb=ωp×argmaxbUmk+ωg×pTm-cUmk+ωh×argmincUmk+eUmk]? ? （12）

于是最稳定分配向量的求解问题最终可以描述为：搜索以公式（12）为目标函数的最优解问题。

3.2 L-PSO的求解算法描述

PSO算法是一种基于群体智能的全局随机搜索算法，具有规则简单、实现容易、精度高和收敛快等特点[11]。在解决最优团队选择问题方面，与差分进化（Differential Evolution，DE）算法相比，PSO算法具有以下优势：PSO算法的全局收敛能力相比较弱，但求解离散点最优解问题的能力较强[11];离散粒子群算法能够更好地解决具有局部聚集特征的最优团队选择问题[12];PSO算法更加成熟，参数设置难度较低，并能夠更好地保证求解质量。

基本的PSO算法往往会陷入局部最优，需要引入一种策略扩大搜索范围，增加种群多样性。采用L-PSO的算法作为最稳定分配向量的求解算法，对基于L-PSO的算法改进和应用过程描述如下：

1）初始种群的编码过程及表达形式。

[Ms]集合的第i个元素[Mi][Mι]的分配向量可表示为

[Mι=ΔTmx1ix2i?xmiΔS1ΔS2…ΔSnc1i1+e1i1c1i2+e1i2…c1in+e1inc2i1+e2i1c2i2+e2i2…c2in+e2in??…?cmi1+emi1cmi2+emi2…cmin+emin]

[ΔSn]表示[Sn]用于联盟的支出和任务的开销，当[cpik+epik=0，p∈1，m，k∈[1，n]]时，表示[Sk]不参与完成[Tp]。于是[Ml]的编码规则可描述为：

[Mι=x1i，…，xmi，…，]。

2）给出加入惯性权重的基本粒子群形式。

已知泛集群数量[N=Sn]，粒子数量为P，由所有联盟结构的分配向量组成离散点集合[X]，则第[j]个粒子[j

[Vjd+1=vVjd+c1ζpjd-Xjd+c2ηpgd-Xjd]? ? （13）

[Xjd+1=Xjd+Vjd+1]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（14）

为了防止速度过快而直接飞过最优解，算法引入[?]表示惯性权重用于决定粒子的当前速度;给定[c1，c2∈0，2]表示学习因子，表示向全局最优的学习能力;均匀随机数[ζ，η=Rand0，1];[Vjd+1]取决于[Vjd，pjd，pgd]。

3）离散化L-PSO算法。

由于[X]为非连续的样本集合，因此首先给出PSO算法的离散化表述形式如公式（15）-（16）所示。

[Vjd+1=vVjd+c1ζpjd-Xjd+c2ηpgd-Xjd]? ?（15）

[Xjd+1=Xjd⊕Vjd+1]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（16）

作为一种非高斯随机过程，莱维飞行[4，12-14]具有以下特点：发生长程跳远[14];具有马尔可夫性质[15];过程随机性[15]。莱维飞行可描述为公式（17）形式。

[Ls，γ，μγ2π×exp-γ2s-μ×s-μ320<μ

其中[μ]为位移参数，[γ>0]为尺度参数，将其离散化并得到公式（18）形式。

[Xjd+1=Xjd+ξ⊕Ls，γ，μ]? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（18）

其中[Ls，γ，μ]决定行进方向和步长，转移概率[ξ]和[d]代位置将决定[d+1]代的位置。以公式（19）模拟莱维分布的随机搜索路径并进一步离散化[Ls，γ，μ]。

[Ls，γ，μ=μ/u1β]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （19）

给定[β=1.5][13]，因此离散莱维飞行可更新为公式（20）描述形式。

[Xjd+1=Xjd+ξ⊕0.01μu1βXjd+1-pgworst]? ? ? ? ? ? （20）

[pgworst]表示上一次迭代的劣勢解，[W：N0，1]，[β：N0，σ2μ]。公式（20）的目的是增加种群多样性，为保证这种多样性，以[Xjd+1-pgworst]作为交换序集合[W]，[W]中因子发生的概率[Prob]将由因子[τ=μu1β]决定，并可表示为公式（21）。

[Prob=τ/Stepsizemax-Stepsizemin]? ? ? （21）

其中[Stepsizemax=maxτ，Stepsizemin=minτ]，至此完成L-PSO的离散化。

4）给出基于L-PSO的最稳定联盟体[Ms-best]，算法的详细计算步骤如算法2描述。

[算法2 L-PSO的最稳定联盟体选择 Input [U，c1，c2，d，X] Output [Ms-best] 1： Begin 2： define [pgworst，pj，pg，V]; 3： for d

4 实验对比

4.1 实验准备

1）样本描述：在油田化学化工领域，计算高分子准晶体纳米结构的弱互斥力对分子稳定性的影响程度时，通常选用[OBR25]（6，12，15）、[OBR40]（24，6，6）和[SEVR]（12，3，30）作为弱互斥力计算函数，括号内数值分别表示这三种函数的维度（[dimensionality，dim]）、阶数（[power，pow]）、单次线性操作数（[operation，op]）。三种函数的维度、阶数和单次线性操作数差别较大，实验对比效果明显，具有一定的代表性，因此选用这三种函数作为实验的测试实例。设定整体任务的总效用为100，可分解为7个独立任务，给出第m个独立任务[Tm]的效用为：

[pTm=3m，m∈1，637，m=7]

2）环境构建：在一个由两级交换机组成的网络覆盖区域内，每一个二级交换机及下属的所有工作终端可视为一个泛集群，共计18个泛集群。

3）算法的基本参数设置：除理性因子的影响力实验外，设定理性期望绝对倾向联盟理性，即[ωp=0.2]、[ωh=0.7];在剔除谈判无关联盟的实验中，初始随机点数量的取值范围[v∈2，18]，累计17次实验;在L-PSO算法的性能测试实验中，设定学习因子[c1，c2]为均匀随机数[Rand0，2]，飞行最大速度[vmax=90]，惯性权重为0.4，迭代次数[d=1000]。

4.2 算法性能的对比分析

选用差分进化算法（Differential Evolution， DE）[2]作为对比算法，其应用场景和求解意图与L-PSO算法相似。两种算法的对比测试包括搜索速度测试、求解质量和稳定性测试及收敛性测试。

4.2.1 搜索速度测试（平均计算时间对比）

随机选择并记录10次测试过程，三种测试实例在L-PSO和DE算法中的平均计算时间及±95%置信区间[5]时间如表1所示（单位为毫秒）。

由表1数据可知，L-PSO算法计算测试实例SEVR的平均时间略低于DE算法，表明L-PSO算法计算高操作数的测试实例速度更快;两种算法计算测试实例OBR25的平均时间基本一致，说明两种算法对于高阶测试实例的计算速度是相同的;而对于高维度的测试实例OBR40，L-PSO算法的计算时间明显高于DE算法。

4.2.2 求解质量和稳定性测试

随机选择并记录10次测试过程，三种测试实例通过L-PSO和DE算法计算获得的平均联盟体效用和标准差如表2所示。由表2数据可知，对于测试实例SEVR和OBR25，L-PSO算法获得的平均联盟体效用始终高于DE算法;而对于测试实例OBR40，L-PSO算法获得的平均联盟体效用普遍略低于DE算法。

表3给出了三种测试实例在两种算法中的8项重要测试数据，其中联盟体效用极值[vmaxM]作为衡量求解质量的标准，[vmaxM]越大，优化质量越出色;方差[Λ]描述了算法的绝对稳定性，[Λ]越小，算法的绝对稳定性越高。

对于测试实例SEVR和OBR25，L-PSO算法获得的最优联盟体效用极值相比DE算法提高了8%-10%，表明L-PSO算法在低维度测试实例的优化质量优于DE算法;对于测试实例OBR40，L-PSO算法获得的最优联盟体效用极值相比DE算法下降了2.4%，表明DE算法在高维度测试实例的优化质量略优于L-PSO算法;两种算法的[Λ]值相差幅度小于4%，表明两种算法的绝对稳定性差异较小，但L-PSO算法的[Λ]值最小，表明其绝对稳定性略优于DE算法。

4.2.3 收敛性测试

根据表3进一步分析两种算法的收敛性：定义取得极值前相邻两次联盟体效用差值[εa，a-1=va-va-1];极值差[E=vmaxM-vminM]，反应了算法的相对稳定性;第[a]次迭代的峭度[K=εa，a-1/E]，峭度越小，收敛性越好。

取误差[ε=vmaxM-vaMvmaxM<0.005]，表4给出在取得极值时的测试结果，分析并给出如下说明：（1）在不同的测试实例中，DE算法的峭度值始终高于L-PSO算法，说明DE算法的收敛性略高于L-PSO算法;（2）L-PSO算法的极值差[E]始终小于DE算法，说明L-PSO的相对稳定性高于DE算法。

4.3 不同理性因子的效果对比

分别测试在不同主观意愿下，不同泛集群数量组成最优联盟体的效用情况。测试要求保持任务数量不变;泛集群数量[k∈7，18];参与测试的主观意愿倾向集合如表4所示。L-PSO算法對维度较为敏感，同时高阶数的测试实例将使实验的时空复杂度呈几何级数增长，加重了实验噪音因素的影响，因此综合考虑选用维度较高、阶数较低的SEVR作为不同理性因子的效果对比实验的测试实例。

测试结果如图1所示，[vmaxM]出现的位置取决于泛集群的数量和[ωh]值，因此可以得到以下结论：联盟理性倾向越高，越适合泛集群数量多的环境;[vmaxM]的极大值将出现在[ωp?ωh]时，此时联盟体的稳定性和性价比最高;此外，不同理性因子所取得的[vmaxM]浮动不大，说明基本理性期望满足的主观意图是联盟理性。

5 结束语

作为一种新型计算环境，泛集群将成为未来普适计算解决大规模科学计算问题的重要手段，而解决多个泛集群间的协同作业问题也是推进这一领域发展的重要研究内容。本文以泛联盟的形成为背景，研究最优联盟体的求解方法，并通过实例测试验证了方法的有效性，为解决多任务下的多集群协作问题提供了一种新的解决方案。

本文提出的方法在应对谈判反噬效应和解决局部离散点聚集问题依旧存在有待完善之处，例如如何找到最优[v]解和聚集特征因素的搜索等，这也是下一步需要继续研究的课题。

参考文献：

[1] Ueda S， Iwasaki A， Conitzer V， et al. Coalition structure generation in cooperative games with compact representations[J]. Autonomous Agents and Multi-Agent Systems， 2018（6）： 1-31.

[2] Ali M， Siarry P， Pant M. An efficient Differential Evolution based algorithm for solving multi-objective optimization problems[J]. European Journal of Operational Research， 2018， 217（2）： 404-416.

[3] Zhao Q， Zhang L Y. Research on the Effect of DPSO in Team Selection Optimization under the Background of Big Data[J]. Complexity， 2018， 2018（8）： 1-14.

[4] 桂海霞，蒋建国，张国富. 面向并发多任务的重叠联盟效用分配策略[J]. 模式识别与人工智能， 2016， 29（4）： 332-340.

[5] Zhang G F， Su Z， Li M， et al. A Task-Oriented Heuristic for Repairing Infeasible Solutions to Overlapping Coalition Structure Generation[J]. IEEE Transactions on Systems Man & Cybernetics Systems， 2017，（99）： 1-17.

[6] Liu Y， Zhang G F， Su Z P， et al. Using Computational Intelligence Algorithms to Solve the Coalition Structure Generation Problem in Coalitional Skill Games[J]. Journal of Computer Science and Technology， 2016， 31（6）： 1136-1150.

[7] Zhang G， Yang R， Su Z， et al. Using binary particle swarm optimization to search for maximal successful coalition[J]. Applied Intelligence， 2015， 42（2）： 195-209.

[8] Hakl? H， U?uz H. A novel particle swarm optimization algorithm with Lévy flight[J]. Applied Soft Computing Journal， 2014， 23（5）： 333-345.

[9] Branzei R， Dimitrov D， Tijs S. Models in Cooperative Game Theory[M]. Springer Berlin Heidelberg， 2005.

[10] Goyal T， Kaushal S. An Intelligent Scheduling Scheme for Real-Time Traffic management using Cooperative Game Theory and AHP-TOPSIS methods for Next Generation Telecommunication Networks[J]. Expert Systems with Applications， 2017（86）： 125-134.

[11] Pandit D， Zhang L， Chattopadhyay S， et al. A Scattering and Repulsive Swarm Intelligence Algorithm for Solving Global Optimization Problems [J]. Knowledge-Based Systems， 2018（156）： 12-42.

[12] 李荣雨，王颖. 基于莱维飞行的改进粒子群算法[J]. 系统仿真学报， 2017， 29（8）： 1685-1691.

[13] Chechkin A V， Metzler R， Klafter J， et al. Introduction to the theory of Lévy flights[C]. Anomalous Transport： Foundations and Applications. Weinheim： John Wiley Sons， 2008： 129-162.

[14] Yang X S. Cuckoo search via Lévy flights[C]. World Congress on Nature & Biologically Inspired Computing. Coimbatore： IEEE， 2009： 210-214.

[15] Souidi M， Piao S， Li G， et al. Coalition formation algorithm based on organization and Markov decision process for multi-player pursuit evasion[J]. Multiagent & Grid Systems， 2015， 11（1）： 1-13.

【通联编辑：谢媛媛】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。